No CrossRef data available.
Published online by Cambridge University Press: 28 April 2014
One way of expressing the self-duality 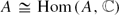 $A\cong {\rm Hom}(A,\mathbb{C})$ of Abelian groups is that their character tables are self-transpose (in a suitable ordering). In this paper we extend the duality to some noncommutative groups considering when the character table of a finite group is close to being the transpose of the character table for some other group. We find that groups dual to each other have dual normal subgroup lattices. We show that our concept of duality cannot work for non-nilpotent groups and we describe p-group examples.
$A\cong {\rm Hom}(A,\mathbb{C})$ of Abelian groups is that their character tables are self-transpose (in a suitable ordering). In this paper we extend the duality to some noncommutative groups considering when the character table of a finite group is close to being the transpose of the character table for some other group. We find that groups dual to each other have dual normal subgroup lattices. We show that our concept of duality cannot work for non-nilpotent groups and we describe p-group examples.