No CrossRef data available.
Published online by Cambridge University Press: 24 October 2008
In (4) a space C of generalized functions was defined which is rather larger than the simple space used to such effect by Lighthill in (3). At the core of C is the space C0 = T of test functions. These are entire (complex) functions f such that all derivatives of f and its Fourier transform F have order of magnitude not exceeding 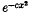 as x → ± ∞, where c is a positive number depending on the individual derivative concerned. If f, g∈ T, the inner product 〈f | g〉 is defined to be
as x → ± ∞, where c is a positive number depending on the individual derivative concerned. If f, g∈ T, the inner product 〈f | g〉 is defined to be
