Published online by Cambridge University Press: 24 October 2008
The following paper is in two parts.
In Part 1 it is shown that Kronecker's theorem can be extended in the form
If 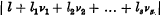 is greater than ηfor all sets of integers l1, l2, … l3 less in absolute value than K/σ and not all zero, l also being an integer, then, for any x1, x2 … x3, an integer q less than l/(ησ8) can be found such that qv1–x1, qv2–x2…qv3–x4 all differ from integers by less than σ;. K, L depend only on s.
is greater than ηfor all sets of integers l1, l2, … l3 less in absolute value than K/σ and not all zero, l also being an integer, then, for any x1, x2 … x3, an integer q less than l/(ησ8) can be found such that qv1–x1, qv2–x2…qv3–x4 all differ from integers by less than σ;. K, L depend only on s.
It is an immediate corollary that if
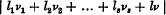
is greator than 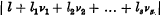 for all sets of integers l1, l2… l3, l less in absolute value than K/σ and not all zero while F(v1, v2… v3), l less in absolute value than K/σ and not all zero while F(v1, v2… v3, v) is periodic period 1, in v1, v2 … v3,v, then T can be found between 0 and
for all sets of integers l1, l2… l3, l less in absolute value than K/σ and not all zero while F(v1, v2… v3), l less in absolute value than K/σ and not all zero while F(v1, v2… v3, v) is periodic period 1, in v1, v2 … v3,v, then T can be found between 0 and 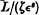 such that
such that
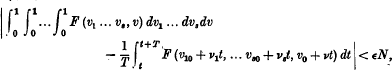
Where K, L depend on s, and N on s and the bounds of
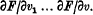
* Landau, E., Scripta Universitatis atque Bibliothecae Hierosolymitanarum; 1923, Über Diophantische Approximationen.Google Scholar
* Burgers, , Proc. Amsterdam Roy. Acad. of Sciences, 20, p. 163.Google Scholar
† Dirac, P. A. M., Proc. Roy. Soc. A, 107, p. 725.CrossRefGoogle Scholar
‡ Laue, M., Ann. der Physik, 4te Folge, 76, p. 619.Google Scholar