Published online by Cambridge University Press: 24 October 2008
For a real number λ, ‖λ‖ is the absolute value of the difference between λ and the nearest integer. Let X represent the m-tuple (x1, x2, … xm) and let
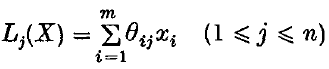
be any n linear forms in m variables, where the Θij are real numbers. The following is a classical result of Khintchine (1):
For all pairs of positive integers m, n there is a positive constant Г(m, n) with the property that for any forms Lj(X) there exist real numbers α1, α2, …, αn such that
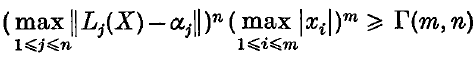
for all integers x1, x2, …, xm not all zero.