Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-28T02:03:05.674Z Has data issue: false hasContentIssue false
  • English
  • Français

Analysis of tangential properties of curves of infinite length

Published online by Cambridge University Press:  24 October 2008

A. S. Besicovitch
A. S. Besicovitch
Affiliation:
Trinity CollegeCambridge
Get access Rights & Permissions [Opens in a new window]

Extract

In a recent paper (1) I have studied tangential properties of sets of infinite measure. This note represents a complementary study of sets and, in particular of arcs, of σ-finite linear measure. Suppose we have a linearly measurable set E of infinite measure that can be represented as the sum 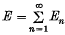of sets of finite measure. Write En = En, 1 + En, 2, where En, 1 is the set of regular points of En and En, 2 that of irregular ones. The set F = ΣEn, 1 is a regular component of E and the set G = ΣEn, 2 an irregular one. A tangent toEn exists at almost all points of En, 1 and at almost no points of En, 2. Denote by Tn the set of all tangents to En and by T the sum-set ΣTn. T will be called a tangent-set to E. Lines of T are defined corresponding to almost all points of F and to the points of a subset of G of measure zero.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 53 , Issue 1 , January 1957 , pp. 69 - 72
Copyright
Copyright © Cambridge Philosophical Society 1957

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Besicovitch, A. S.On the definition of tangents to sets of infinite linear measure. Proc. Camb. Phil. Soc. 52 (1956), 20–29.Google Scholar
(2)Besicovitch, A. S.On the fundamental geometrical properties of linearly measurable plane sets of points. Math. Ann. 98 (1928), 422–64.CrossRefGoogle Scholar