Asymptotic estimates of the eigenvalues of certain positive Fredholm operators
Published online by Cambridge University Press: 24 October 2008
Extract
1. Introduction. Suppose that K is a continuous function on the square Q = [ – 1, 1] x [– 1,1] satisfying 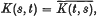 , for – 1 ≤ s, t ≤ 1; then the Fredholm operator T on L2(-1,1)
, for – 1 ≤ s, t ≤ 1; then the Fredholm operator T on L2(-1,1)
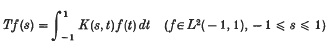
is compact and symmetric. Suppose also that T is a positive operator, i.e.
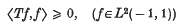
then there is an eigenfunction expansion
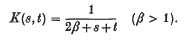
where (λn) is a sequence of non-negative real numbers which decreases to 0 and (φn) is an orthonormal sequence in L2( – 1,1). In this paper we shall find asymptotic estimates for λn when K takes certain specific analytic forms. In all cases K will be real-valued on Q and analytic in a neighbourhood of Q in complex 2-space; for example
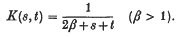
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 91 , Issue 2 , March 1982 , pp. 267 - 284
- Copyright
- Copyright © Cambridge Philosophical Society 1982
References
REFERENCES
- 3
- Cited by


