Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-01-27T19:17:23.860Z Has data issue: false hasContentIssue false
  • English
  • Français

Attractors with irrational rotation number

Published online by Cambridge University Press:  12 December 2011

LUIS HERNÁNDEZ-CORBATO ,
RAFAEL ORTEGA  and
FRANCISCO R. RUIZ DEL PORTAL
LUIS HERNÁNDEZ-CORBATO
Affiliation:
Departamento de Geometría y Topología, Facultad de CC. Matemáticas, Universidad Complutense de Madrid, 28040 Madrid, Spain. e-mail: luishcorbato@mat.ucm.es
RAFAEL ORTEGA
Affiliation:
Departamento de Matemática Aplicada, Facultad de Ciencias, Universidad de Granada, 18071 Granada, Spain. e-mail: rortega@ugr.es
FRANCISCO R. RUIZ DEL PORTAL
Affiliation:
Departamento de Geometría y Topología, Facultad de CC. Matemáticas, Universidad Complutense de Madrid, 28040 Madrid, Spain. e-mail: r_Portal@mat.ucm.es
Get access Rights & Permissions [Opens in a new window]

Abstract

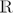Let h: 2 → 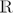2 be a dissipative and orientation preserving homeomorphism having an asymptotically stable fixed point. Let U be the region of attraction and assume that it is proper and unbounded. Using Carathéodory's prime ends theory one can associate a rotation number, ρ, to h|U. We prove that any map in the above conditions and with ρ ∉ 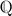induces a Denjoy homeomorphism in the circle of prime ends. We also present some explicit examples of maps in this class and we show that, if the infinity point is accessible by an arc in U, ρ ∉ 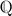if and only if Per(h) = Fix(h) = {p}.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 153 , Issue 1 , July 2012 , pp. 59 - 77
Copyright
Copyright © Cambridge Philosophical Society 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Arrowsmith, D. K. and Place, C. M.. An Introduction to Dynamical Systems (Cambridge University Press, 1992).Google Scholar
[2]Alligood, K. T. and Yorke, J. A.. Accessible saddles on fractal basin boundaries. Ergod. Th. Dynam. Sys. 12 (1992), 377–400.CrossRefGoogle Scholar
[3]Barge, M.. Prime end rotation numbers associated with the Hénon map., In Continuum Theory and Dynamical Systems Lecture Notes in Pure and Appl. Math. vol. 149 (Dekker, 1993), pp. 15–33.Google Scholar
[4]Birkhoff, G. D.. Sur quelques courbes fermées remarquables. Bull. Soc. Math. France 60 (1932), 1–26.Google Scholar
[5]Bonatti, C. and Kolev, B.. Surface homeomorphisms with zero-dimensional singular set. Topology Appl. 90 (1998), 69–95.CrossRefGoogle Scholar
[6]Bonino, M.. A Brouwer-like theorem for orientation reversing homeomorphisms of the sphere. Fund. Math. 182 (2004), no. 1, 1–40.CrossRefGoogle Scholar
[7]Cartwright, M. L. and Littlewood, J. E.. Some fixed point theorems. Annals of Math. 54 (1951), 1–37.CrossRefGoogle Scholar
[8]Hale, J. K.. Asymptotic behavior of dissipative systems. Mathematical Surveys and Monographs, 25 (American Mathematical Society, 1988).Google Scholar
[9]Kerékjártó, B.. Sur le caractèr topologique des représentations conformes. C.R. Acad. Sci. 198 (1934), 317–320.Google Scholar
[10]Levinson, N.. Transformation theory of non-linear differential equations of the second order. Ann. of Math. 45 (1944), 723–737. Addendum: Ann. of Math. 49 (1948), 738.CrossRefGoogle Scholar
[11]Markley, N. G.. Homeomorphisms of the circle without periodic points. Proc. London Math. Soc. 20 (1970), 688–698.CrossRefGoogle Scholar
[12]Mather, J. N.. Topological proofs of some purely topological consequences of Carathéodory's theory of prime ends. Selected Studies. North Holland Publishing Company, Eds. Rassias, Th.M., Rassias, G.M. (1982), 225–255.Google Scholar
[13]Matsumoto, S. and Nakayama, H.. Continua as minimal sets of homeomorphisms of 2. arXiv:1005.0360v1 [math.DS].Google Scholar
[14]Ortega, R. and Ruiz del Portal, F. R.. Attractors with vanishing rotation number. J. Eur. Math. Soc. 13 (2011), 1567–1588.CrossRefGoogle Scholar
[15]Pommerenke, Ch.. Boundary behaviour of conformal maps. Lecture Notes in Math. (Springer-Verlag, 1991).Google Scholar