Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Yamagishi, Kikumichi
1994.
Type of blowing-up over a Buchsbaum ring.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 115,
Issue. 3,
p.
407.
Kawasaki, Takesi
1995.
Surjective-buchsbaum modules over cohen-macaulay local rings.
Mathematische Zeitschrift,
Vol. 218,
Issue. 1,
p.
191.
Yoshida, Ken-ichi
1995.
On linear maximal buchsbaum modules and the syzygy modules.
Communications in Algebra,
Vol. 23,
Issue. 3,
p.
1085.
Yoshida, Ken-ichi
1996.
A note on minimal cohen-macaulay approximations.
Communications in Algebra,
Vol. 24,
Issue. 1,
p.
235.
Yoshida, Ken-ichi
1997.
A note on multiplicity of perfect modules of codimension one.
Communications in Algebra,
Vol. 25,
Issue. 9,
p.
2807.
Yoshida, Ken-Ichi
1998.
A generalization of linear buchsbaum modules in terms of homological degree.
Communications in Algebra,
Vol. 26,
Issue. 3,
p.
931.
Yamagishi, Kikumichi
2002.
Buchsbaumness in Rees Modules Associated to Ideals of Minimal Multiplicity in the Equi-I-Invariant Case.
Journal of Algebra,
Vol. 251,
Issue. 1,
p.
213.
Yamagishi, Kikumichi
2003.
Buchsbaumness in the Rees modules associated to m-primary ideals in the one-dimensional case.
Journal of Pure and Applied Algebra,
Vol. 181,
Issue. 2-3,
p.
309.
Nagel, Uwe
2005.
Liaison classes of modules.
Journal of Algebra,
Vol. 284,
Issue. 1,
p.
236.
Vasconcelos, Wolmer V.
2013.
Commutative Algebra.
p.
667.


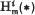 stands for the
stands for the 