A better than 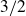$3/2$ exponent for iterated sums and products over 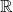$\mathbb R$

Abstract

In this paper, we prove that the bound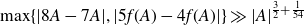

\begin{equation*}\max \{ |8A-7A|,|5f(A)-4f(A)| \} \gg |A|^{\frac{3}{2} + \frac{1}{54}}\end{equation*}

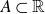holds for all $A \subset \mathbb R$, and for all convex functions f which satisfy an additional technical condition. This technical condition is satisfied by the logarithmic function, and this fact can be used to deduce a sum-product estimate

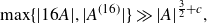\begin{equation*}\max \{ |16A|, |A^{(16)}| \} \gg |A|^{\frac{3}{2} + c},\end{equation*}

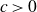for some $c\gt 0$. Previously, no sum-product estimate over 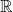$\mathbb R$ with exponent strictly greater than 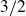$3/2$ was known for any number of variables. Moreover, the technical condition on f seems to be satisfied for most interesting cases, and we give some further applications. In particular, we show that

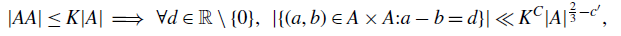\begin{equation*}|AA| \leq K|A| \implies \,\forall d \in \mathbb R \setminus \{0 \}, \,\, |\{(a,b) \in A \times A : a-b=d \}| \ll K^C |A|^{\frac{2}{3}-c^{\prime}},\end{equation*}

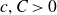where $c,C \gt 0$ are absolute constants.

1. Introduction

Given a finite set $A \subset \mathbb R$ , let $A+A$ and AA denote the sum set and product set of A respectively. That is,

\begin{equation*}A+A\,:\!=\, \{a+b \,:\, a,b \in A \}, \,\,\,\,\,\,\,\,AA\,:\!=\, \{ab \,:\, a,b \in A \}.\end{equation*}

The Erdős–Szemerédi [ 4 ] sum-product conjecture states that, for all $\epsilon \gt 0$ , the bound

(1) \begin{equation} \max \{ |A+A|, |AA| \} \geq |A|^{2- \epsilon}\end{equation}

holds for all sufficiently large $A \subset \mathbb N$ .

One can also consider an analogue of the Erdős–Szemerédi conjecture with more variables. The notation kA and $A^{(k)}$ are used for the k-fold sum set and k-fold product set respectively. That is,

\begin{equation*}kA\,:\!=\, \{a_1+ \dots + a_k \,:\, a_1,\dots,a_k \in A \}, \,\,\,\,\,\,\,\,A^{(k)}\,:\!=\, \{a_1 \cdots a_k \,:\, a_1,\dots,a_k \in A \}.\end{equation*}

An analogue of (1) for the k-fold sum and product sets was also considered in [ 4 ]. An outstanding result of Bourgain and Chang [ 1 ] establishes that one of the iterated sum set or product set must exhibit unbounded growth. They proved that, for all $h \in \mathbb N$ , there exists $k \in \mathbb N$ such that

(2) \begin{equation} \max \left\{ |kA|, |A^{(k)}| \right\} \geq |A|^{h}\end{equation}

holds for all $A \subset \mathbb N$ . See also [ 10 ] for an alternative and more easily digestible proof of the Bourgain–Chang Theorem.

The sum-product problem can also be studied for $A \subset \mathbb R$ , and indeed most contemporary work on the conjectured bound (1) uses geometric arguments that hold over the reals. The current best estimate towards this conjecture is the bound ¹

\[\max\left\{|A+A|,|AA| \right\} \gg |A|^{\frac{4}{3}+ \frac{2}{1167}-o(1)},\]

due to Rudnev and Stevens [ 8 ]. This estimate holds for all $A \subset \mathbb R$ , and no quantitative improvements are known if we instead consider an arbitrary set A of integers.

On the other hand, progress for the real k-fold analogue of the Erdős–Szemerédi Conjecture lags far behind the best-known results over $\mathbb N$ . For instance, the bound (2) is not known to hold even for $h=3/2$ for $A \subset \mathbb R$ , at which point the dominant geometric methods appear to reach their limitation.

The main result of this paper gives some progress for this problem, pushing the growth exponent for the k-fold sum-product problem beyond the threshold $3/2$ .

Theorem 1·1. There exists an absolute constant $c\gt 0$ such that, for any finite set $A \subset \mathbb R$

\begin{equation*}\max \{ |16A|, |A^{(16)}| \} \geq |A|^{\frac{3}{2}+c}.\end{equation*}

Theorem 1·1 is a special case of a more general result (see the forthcoming Theorem 5·1) concerning the relationship between convexity and sum sets. The guiding idea here is that strictly convex or concave functions disturb any additive structure existing in a set. This idea has been explored in several papers, including the pioneering work of Elekes, Nathanson and Ruzsa [ 3 ], who broke new ground using incidence theory.

Recently, a new elementary method was introduced by Solymosi (see [ 9 ]) which has enabled further progress. This “squeezing” technique was used in [ 5 ] to prove that the bound

(3) \begin{equation} |A+A-A||f(A)+f(A)-f(A)| \gg \frac{|A|^3}{\log|A|}\end{equation}

holds for all $A \subset \mathbb R$ . A further improvement, removing the logarithmic factor, was later given by Bradshaw [ 2 ]. This technique has also been used in [ 6 ] to give improved bounds for the number of distinct dot products determined by a point set in $\mathbb R^2$ . The same squeezing technique is the main tool for this paper, and a closer analysis allows for an improvement to the bound (3) by introducing more variables, provided that the convex function f satisfies an additional technical condition.

As another application of our general result, we prove the following result concerning the number of additive representations for sets with small multiplicative doubling.

Theorem 1·2. There exist absolute constants $c,C\gt 0$ such that, for any finite set A of positive reals and any $t \in \mathbb R \setminus \{0 \}$ ,

\begin{equation*} |AA| \leq K|A| \implies |\{ (a,b) \in A \times A \,:\, a-b=t \}| \ll K^{C} |A|^{\frac{2}{3}- c} . \end{equation*}

A weaker version of Theorem 1·2, without the constant c, can be proven by a simple application of the Szemerédi-Trotter Theorem. Such results are sometimes referred to in the sum-product community as threshold bounds. Most of these bounds have now been improved by refining and augmenting these basic arguments. Theorem 1·2 represents an improvement for one of the last standing threshold bounds in sum-product theory.

1·1. Notation

Henceforth, all sets introduced in this paper are assumed to be finite unless stated otherwise. We use $\log$ to denote the logarithm function with base 2 and $\ln$ for the logarithmic function with base e. As mentioned in an earlier footnote, throughout this paper, the notation $X\gg Y$ , $Y \ll X,$ $X=\Omega(Y)$ , and $Y=O(X)$ are all equivalent and mean that $X\geq cY$ for some absolute constant $c\gt 0$ . $X \gg_a Y$ means that the implied constant is no longer absolute, but depends on a.

2. Preliminary results

The main external result that will be used in this paper is taken from [ 2 ], and concerns the growth of iterated sum sets of f(A) when f is a highly convex function and A has small additive growth.

For an interval I, we say $f \,:\, I \rightarrow \mathbb R$ is a 0-convex function if it is strictly monotone on I, and in general, f is k-convex on I if each of the derivatives $f^{(1)}, \dots, f^{(k+1)}$ exists and, for all $x \in I$ and $1 \leq j \leq k+1$ , $f^{j}(x) \neq 0$ (hence all but the last derivative are strictly monotone).

Theorem 2·1. Let A be a finite set of real numbers contained in an interval I and let $f\,:\,I \rightarrow \mathbb R$ be a function which is k-convex, for some $k \geq 1$ . Suppose that $|A + A - A| \leq K|A|$ . Then

\begin{equation*}\big|2^kf(A) - (2^k-1)f(A)\big| \geq \frac{ |A|^{k+1}}{(CK)^{2^{k+1}-k-2}}\end{equation*}

for some absolute constant $C \gt 0$ .

Theorem 2·1 represents and improvement to an earlier result from [ 5 ] by removing all logarithmic factors.

We will use the following result of Elekes, Nathanson and Ruzsa [ 3 ].

Theorem 2·2. Let I be an interval, let $f\,:\,I \rightarrow \mathbb R$ be a strictly convex or concave function, and suppose that $A \subset I$ . Then, for all $k \in \mathbb N$ ,

\begin{equation*}|kA| |kf(A)| \gg |A|^{3-2^{1-k}}.\end{equation*}

Setting $f(x)= \ln x$ in Theorem 2·2 establishes that the bound (2) holds over the reals for all $h \lt 3/2$ . The proof of Theorem 2·2 uses a variant of the Szemerédi–Trotter Theorem applied iteratively.

We will use the Plünnecke–Ruzsa Theorem to control the growth of iterated sum sets.

Theorem 2·3. Let X and Y be sets in an abelian group. Then for any non-negative integers k and l such that $k+l \gt 1$ ,

\begin{equation*}|kX-lX| \leq \frac{ |X+Y|^{k+l}}{|Y|^{k+l-1}}.\end{equation*}

We will also use the following form of the Ruzsa Triangle Inequality.

Theorem 2·4 For any sets X,Y,Z in an abelian group,

\begin{equation*}|Y-Z|\leq\frac{|X+Y||X+Z| }{|X|}.\end{equation*}

3. The main general result

All of the results mentioned in the introduction are derived from the forthcoming Theorem 3·1, and the purpose of this section is to state and prove this result.

Before doing so, we need to introduce the function $f_d$ , which is central to this paper. Let $a \in \mathbb R$ and let I denote the interval $I=(a, \infty)$ . Suppose that $f\,:\, I \rightarrow \mathbb R$ is a strictly convex or concave function. Let d be a strictly positive real number. Define the function

\begin{equation*}f_d\,:\, I \rightarrow J, \,\,\,\,\, f_d(x)\,:\!=\,f(x+d)-f(x).\end{equation*}

Here J denotes the range of $f_d$ , and J is always an interval. Since f is strictly convex or concave, it follows that the function $f_d$ is monotone. In particular, the inverse function $f_d^{-1}\,:\,J \rightarrow I$ is defined.

Theorem 3·1. Let $a \in \mathbb R$ , let I denote the interval $I=(a, \infty)$ , and let $m \in \mathbb N$ . Suppose that $A \subset I$ is a finite set. Suppose that $f\,:\,(a, \infty) \rightarrow \mathbb R$ is a strictly convex or concave function. Suppose also that, for any $d \in (0, \infty)$ , the function $f_d^{-1}\,:\, J \rightarrow I$ has the property that its first three derivatives have a combined total of at most m zeroes. Then

(4) \begin{equation} |8A-7A|^{16}|5f(A)-4f(A)|^{11} \gg_m |A|^{41}.\end{equation}

In particular,

(5) \begin{equation} \max \{|8A-7A|, |5f(A)-4f(A)| \} \gg_m |A|^{\frac{3}{2} +\frac{1}{54}}.\end{equation}

Proof. The inequality (5) follows from (4) by the pigeonhole principle. Therefore, it is sufficient to prove (4). We will consider the case where f is strictly convex only. For strictly concave f, the same proof works with some minor modifications. Write $A=\{a_1\lt \dots \lt a_n \}$ . Given $d \in \mathbb R$ , define

\begin{equation*}A_d\,:\!=\, \{ a_i \in A \,:\, a_{i+1} - a_i=d \}.\end{equation*}

Claim 1. There exists a set D ^′ such that

(6) \begin{equation} \sum_{d \in D^{\prime}} |A_d| \geq \frac{n}{6},\end{equation}

and, for all $d \in D^{\prime}$ ,

(7) \begin{equation} |A_d| \geq \frac{n^2}{12|A+A-A|}.\end{equation}

Proof of Claim 1. Order the indices $i \in [n-1]$ in ascending order according to the value $a_{i+1}-a_i$ , with ties broken arbitrarily. Let $\mathcal I$ denote the first $\lfloor n/2 \rfloor - 1$ indices, and let $\mathcal J$ denote the remaining indices. Observe that $|\mathcal J| \geq n/2$ . Define

\begin{equation*}D\,:\!=\, \{ a_{i+1}-a_i \,:\, i \in \mathcal I \}.\end{equation*}

It follows from this ordering that, for all $ i \in \mathcal I$ and $j \in \mathcal J$

\begin{equation*}a_{i+1}- a_{i} \leq a_{j+1} - a_j.\end{equation*}

Therefore, for each $j \in \mathcal J$ ,

\begin{equation*}\{a_j + d \,:\, d \in D \} \subset (a_j, a_{j+1}].\end{equation*}

Hence we obtain $|D|$ elements of $A+A-A$ in the interval $(a_j, a_{j+1}]$ . Since these intervals are disjoint, we can repeat this argument for all $j \in \mathcal J$ to obtain

\begin{equation*}|A+A-A| \geq \sum_{j \in \mathcal J} |D| \geq \frac{|D|n}{2}.\end{equation*}

A rearrangement of this inequality gives the bound

(8) \begin{equation} |D|\leq \frac{2|A+A-A|}{n}.\end{equation}

Next, observe that

(9) \begin{equation} \sum_{d \in D} |A_d| \geq |\mathcal I| \geq n/3.\end{equation}

Define

\begin{equation*}D^{\prime}\,:\!=\, \left\{ d \in D \,:\, |A_d| \geq \frac{n}{6|D|} \right \}\end{equation*}

and note that

\begin{equation*}\sum_{d \in D \setminus D^{\prime}} |A_d| \leq |D| \cdot \frac{n}{6|D|} = \frac{n}{6}.\end{equation*}

It therefore follows from (9) that that $\sum_{d \in D^{\prime}} |A_d| \geq {n}/{6}$ , thus proving (6). Finally, it follows from (8) and the definition of D ^′ that, for all $d \in D^{\prime}$ ,

\begin{equation*}|A_d| \geq \frac{n}{6|D|} \geq \frac{n^2}{12|A+A-A|}.\end{equation*}

Claim 1 allows us to henceforth assume that

(10) \begin{equation} |A_d| \geq 8m\end{equation}

holds for all $d \in D^{\prime}$ . Indeed, suppose that this is not the case. Then it follows from the inequality (7) that

\begin{equation*}|A+A-A| \gg \frac{|A|^2}{m},\end{equation*}

which is strong enough to imply the intended bound (4).

Next, we make some additional refinements to the sets $A_d$ . This is done in order to set up a lower bound for iterated sums of f(A).

Recall from the definition at the beginning of this section that $f_d(x)\,:\!=\,f(x+d)-f(x)$ . For a given $d \in D^{\prime}$ , write

\begin{equation*}A_d= \{ a_{i_1}, \dots, a_{i_{M}} \},\end{equation*}

where $i_1 \lt \dots \lt i_M$ . Here, we have used M as a temporary notation for the cardinality of $A_d$ (this is simply done to make the subscript more readable). We assume for simplicity that this number is divisible by 4. Let $A^{\prime}_d$ denote the smallest half of $A_d$ , so

\begin{equation*}A^{\prime}_d= \left\{ a_{i_1}, \dots, a_{i_{M/2}} \right\}.\end{equation*}

Observe that, since f is strictly convex,

\begin{equation*}f_d\big(a_{i_1}\big) \lt \dots \lt f_d\big(a_{i_{M}}\big).\end{equation*}

Define

\begin{equation*}t_d\,:\!=\,f_d\big(a_{i_{M/2}}\big).\end{equation*}

That is, $t_d$ is the largest element of $f_d\big(A^{\prime}_d\big)$ . Hence $f_d\big(A^{\prime}_d\big) \subset (0,t_d]$ .

In the forthcoming argument, it will be helpful to force the elements of $f_d\big(A^{\prime}_d\big)$ to be slightly closer to each other.n For each $a_{i_j} \in A^{\prime}_d$ , the image $f_d\big(a_{i_j}\big)$ belongs to one of the intervals $(0,t_d/2]$ or $(t_d/2,t_d]$ , and so it follows that at least half of the elements $f_d\big(a_{i_j}\big)$ are in the same interval. In order to simplify the notation further, let us assume that the first of these intervals is well populated. In particular, if we define

\begin{equation*}A^{\prime\prime}_d\,:\!=\, \{ a_{i_1}, \dots, a_{i_{M/4}} \},\end{equation*}

then $f_d\big(A^{\prime\prime}_d\big) \subset (0,t_d/2]$ , and it follows that

\begin{equation*}2f_d\big(A^{\prime\prime}_d\big)-2f_d\big(A^{\prime\prime}_d\big) \subset (-t_d,t_d).\end{equation*}

We use the notation $L_d$ for the additive tripling of the set $f_d\big(A^{\prime\prime}_d\big)$ , that is

(11) \begin{equation} |f_d\big(A^{\prime\prime}_d\big)+ f_d\big(A^{\prime\prime}_d\big) - f_d\big(A^{\prime\prime}_d\big) | = L_d|f_d\big(A^{\prime\prime}_d\big)|=L_d|A^{\prime\prime}_d|.\end{equation}

A basic version of the forthcoming argument can be used to prove the bound $|2f(A)-f(A)| \gg \sum_{d \in D^{\prime}} |A_d|^2$ , which can then be combined with the ideas present in the proof of Claim 1 to prove the bound (3), even removing the log factor. The difference in approach for the following claim is that we squeeze an iterated difference set into the gaps, which results in some improvement unless the previously defined parameter $L_d$ is constant. A similar approach was recently used in [ 7 ].

Claim 2.

\begin{equation*} |5f(A)-4f(A)| \gg \sum_{d \in D^{\prime}} |A_d|^2 L_d.\end{equation*}

Proof of Claim 2. Let $d \in D^{\prime}$ and let $E_d$ denote the non-negative elements of $2f_d\big(A^{\prime\prime}_d\big)- 2f_d\big(A^{\prime\prime}_d\big)$ . So, $E_d \subset [0,t_d)$ , and since the difference set is symmetric,

(12) \begin{equation} |E_d| \gg \big|2f_d\big(A^{\prime\prime}_d\big)-2f_d\big(A^{\prime\prime}_d\big)\big| \geq \big|2f_d\big(A^{\prime\prime}_d\big)-f_d\big(A^{\prime\prime}_d\big)\big|.\end{equation}

Now, let $M/2 \lt j \leq M$ and consider the set of sums

(13) \begin{equation} f\left(a_{i_j}\right) + E_d \subset \big[f\big(a_{i_j}\big), f\big(a_{i_j}\big)+t_d\big) \subset \big[f\big(a_{i_j}\big), f\big(a_{i_j+1}\big)\big).\end{equation}

The first inclusion above is valid because $E_d \subset [0,t_d)$ . The second is equivalent to the inequality

(14) \begin{equation} f\big(a_{i_j}\big)+t_d \leq f\big(a_{i_j+1}\big).\end{equation}

Since $a_{i_j} \in A_d$ , it follows that $a_{i_j+1}=a_{i_j}+d$ , and so the inequality (14) can be written as $f_d\big(a_{i_j}\big)\geq t_d =f_d\big(a_{i_{M/2}}\big)$ . This is valid, since $f_d$ is monotone increasing and $j \gt M/2$ . We have thus verified the inclusion (13).

On the other hand, it follows from the construction of the set $E_d$ that $E_d \subset 4f(A)-4f(A)$ , and therefore

\begin{equation*}f\big(a_{i_j}\big) + E_d \subset (5f(A)-4f(A) ) \cap \big[f\big(a_{i_j}\big), f\big(a_{i_j+1}\big)\big).\end{equation*}

We have thus identified $|E_d|$ elements of $5f(A)-4f(A)$ lying in between consecutive elements of f(A). We repeat this process for each $M/2 \lt j \lt M$ , and then for each $d \in D^{\prime}$ , yielding

\begin{align*}|5f(A)-4f(A)| \geq \sum_{d \in D^{\prime}} \frac{|A_d|}{2} |E_d| & \gg \sum_{d \in D^{\prime}} |A_d| \big|2f_d\big(A^{\prime\prime}_d\big)-f_d\big(A^{\prime\prime}_d\big)\big|\\& \gg \sum_{d \in D^{\prime}} |A_d|^2L_d.\end{align*}

This completes the proof of the claim.

Before moving on to use Claim 2, let us pause to make a quick remark about its proof. We use the trivial bound

\begin{equation*}\big|2f_d\big(A^{\prime\prime}_d\big)-2f_d\big(A^{\prime\prime}_d\big)\big| \geq \big|2f_d\big(A^{\prime\prime}_d\big)-f_d\big(A^{\prime\prime}_d\big)\big|\end{equation*}

in (12). In principle, it looks like it may be possible to work only with the three variable set $2f_d\big(A^{\prime\prime}_d\big)-f_d\big(A^{\prime\prime}_d\big)$ in this claim. If this argument could be handled successfully, one would be able to replace the set $5f(A)-4f(A)$ in the statement of Theorem 5·1 with the set $4f(A)-3f(A)$ . However, we would like to add only positive elements when employing the squeezing technique. This is where the symmetry of the four variable set $2f_d\big(A^{\prime\prime}_d\big)-2f_d\big(A^{\prime\prime}_d\big)$ is useful, and we were not able to find a way to make this argument work without this symmetry.

Claim 2 gives us some new information unless $L_d$ is very small. However, if this is the case, the next claim allows us to win on the A side. The idea here is that, if $L_d$ really is small, then this implies that some additive structure is buried in f(A), which in turn should imply that A grows under addition.

Claim 3. For any $d \in D^{\prime}$

\begin{equation*}|L_d| \gg \frac{ |A_d|^{4/11}}{m^{15/11}|8A-7A|^{1/11}}.\end{equation*}

Proof of Claim 3. Recall the assumption from the statement of the theorem that the function $f_d^{-1}\,:\,J \rightarrow I$ exists and that its first three derivatives have a total of at most m zeroes. We use these zeroes to divide the domain of $f_d^{-1}$ into $m+1$ pairwise disjoint subintervals $J_1, \dots, J_{m+1} \subset J$ , such that on each of the subintervals, all of the first three derivatives are non-zero.

Let

\begin{equation*}I_1=f_d^{-1}(J_1), \dots, I_{m+1}=f_d^{-1}(J_{m+1}).\end{equation*}

Observe that the intervals $I_1, \dots, I_{m+1} \subset I$ are pairwise disjoint, and that the union $\bigcup_{i=1}^{m+1} I_i$ is equal to the the set I with at most m points removed. Since $A^{\prime\prime}_d \subset I$ , it follows that there is some index i such that

\begin{equation*}|A^{\prime\prime}_d \cap I_i| \geq \frac{|A^{\prime\prime}_d| - m}{m+1} \geq \frac{ |A^{\prime\prime}_d|}{16m} \gg \frac{ |A_d|}{m} .\end{equation*}

The inequality above makes use of 10. Let

\begin{equation*}A^{\prime\prime\prime}_d\,:\!=\, A^{\prime\prime}_d \cap I_i\end{equation*}

and define $g\,:\, J_i \rightarrow I_i$ to be the function $f_d^{-1}$ with the domain restricted to $J_i$ . Since the first three derivatives of g are all non-zero in $J_i$ , the function g is by definition 3-convex. It follows from the definition (11) that

\begin{equation*} \big|f_d\big(A^{\prime\prime\prime}_d\big)+ f_d\big(A^{\prime\prime\prime}_d\big) - f_d\big(A^{\prime\prime\prime}_d\big) \big| \leq \big|f_d\big(A^{\prime\prime}_d\big)+ f_d\big(A^{\prime\prime}_d\big) - f_d\big(A^{\prime\prime}_d\big) \big| = L_d \big|f_d\big(A^{\prime\prime}_d\big)\big| \leq 16mL_d\big|f_d\big(A^{\prime\prime\prime}_d\big)\big|.\end{equation*}

Apply Theorem 2·1 with

\begin{equation*}f=g, \,\,\,\,\,\, k=3, \,\,\,\,\,\, A=f_d\big(A^{\prime\prime\prime}_d\big), \,\,\,\,\,\, K=16mL_d.\end{equation*}

It follows that

\begin{equation*} |8A-7A| \geq \big|8A^{\prime\prime\prime}_d-7A^{\prime\prime\prime}_d\big| \gg \frac{ |A^{\prime\prime\prime}_d|^4}{(mL_d)^{11}} \gg \frac{ |A_d|^4}{m^{15}L_d^{11}}.\end{equation*}

A rearrangement of this inequality gives the claimed bound.

The final task is to combine the inequalities from the previous three claims to complete the proof. By applying Claim 2, Claim 3 and then the two inequalities (7) and (6) from Claim 1, we have

\begin{align*} |5f(A)-4f(A)| \gg \sum_{d \in D^{\prime}} |A_d|^2 L_d &\gg \frac{1}{m^{15/11}|8A-7A|^{1/11}}\sum_{d \in D} |A_d|^{26/11} \\& \gg \frac{1}{m^{15/11}|8A-7A|^{1/11}} \left ( \frac{n^2}{|A+A-A|} \right )^{15/11}\sum_{d \in D} |A_d|\\& \gg \frac{1}{m^{15/11}|8A-7A|^{1/11}} \left ( \frac{n^2}{|A+A-A|} \right )^{15/11} n.\end{align*}

A rearrangement of this gives

\begin{equation*}|8A-7A|^{16}|5f(A)-4f(A)|^{11} \geq |8A-7A| |A+A-A|^{15}|5f(A)-4f(A)|^{11} \gg \frac{n^{41}}{m^{15}}.\end{equation*}

This completes the proof of (4), and therefore also that of Theorem 3·1.

4. Applying Theorem 3·1 for some particular convex functions of interest

Corollary 4·1. Suppose that $A \subset (0, \infty)$ is a finite set. Then

\begin{equation*} \max \left \{|8A-7A|, \left|\frac{AAAAA}{AAAA}\right| \right \} \gg |A|^{\frac{3}{2} +\frac{1}{54}}. \end{equation*}

Proof. Apply Theorem 3·1 with $f(x)= \ln x$ . The function $f_d\,:\,(0, \infty) \rightarrow (0,\infty)$ is defined by

\begin{equation*} f_d(x)= \ln \left ( \frac{x+d}{x} \right). \end{equation*}

Its inverse is

\begin{equation*} f_d^{-1}\,:\,(0, \infty) \rightarrow (0,\infty), \,\,\,\,\,\, f_d^{-1}(x)=\frac{d}{e^x-1}. \end{equation*}

A direct calculation shows that the first three derivatives of $f_d^{-1}$ are non-zero in $(0, \infty)$ . Indeed, the first three derivatives are

\begin{align*} \big(f_d^{-1}\big)^{(1)}(x) & = \frac{-de^x}{(e^x-1)^2}, \\[3pt] \big(f_d^{-1}\big)^{(2)}(x) &= \frac{de^x (e^x+1)}{(e^x-1)^3}, \\[3pt] \big(f_d^{-1}\big)^{(3)}(x) &= \frac{-de^x \big(e^{2x}+4e^x+1\big)}{(e^x-1)^4} . \end{align*}

In this case, the condition that A consists only of positive elements is not significant. For an arbitrary finite set $A \subset \mathbb R$ , at least $({|A|-1})/{2}$ of the elements have (strictly) the same sign. let $A^{\prime} \subset A$ be a set with size at least $({|A|-1})/{2}$ such that all elements of A ^′ have the same sign. If $A^{\prime} \subset (0, \infty)$ then apply Corollary 4·1 to A ^′. Otherwise, it can be applied to $-A^{\prime}$ to give the same result.

Corollary 4·2. Let $\lambda$ be any strictly positive real number and suppose that $X \subset (0, \infty)$ is a finite set. Then

\begin{equation*} \max \left \{\left|\frac{X^{(8)}}{X^{(7)}} \right |, \left|\frac{(X+\lambda)^{(5)}}{(X+\lambda)^{(4)}}\right| \right \} \gg |X|^{\frac{3}{2} +\frac{1}{54}}. \end{equation*}

Proof. Apply Theorem 3·1 with $A= \ln X$ and $f(x)= \ln (e^x+\lambda)$ . The function $f_d\,:\, \mathbb R \rightarrow (0,d)$ is defined by

\begin{equation*} f_d(x)= \ln \left ( \frac{e^{x+d}+\lambda}{e^x+ \lambda} \right). \end{equation*}

Its inverse is

\begin{equation*} f_d^{-1}\,:\,(0, d) \rightarrow \mathbb R, \,\,\,\,\,\, f_d^{-1}(x)= \ln \left ( \frac{\lambda(e^{x}-1)}{e^d-e^x} \right). \end{equation*}

The first three derivatives of $f_d^{-1}$ are

\begin{align*} \big(f_d^{-1}\big)^{(1)}(x) & = \frac{\big(e^d-1\big)e^x}{(e^x-1)\big(e^d-e^x\big)}, \\ \big(f_d^{-1}\big)^{(2)}(x) &= \frac{\big(e^d-1\big)e^x\big(e^{2x}-e^d\big)}{(e^x-1)^2\big(e^d-e^x\big)^2}, \\ \big(f_d^{-1}\big)^{(3)}(x) &= \frac{\big(e^d-1\big)e^x\big[e^{4x}+(e^d+1)e^{3x}-6e^de^{2x}+\big(e^{2d}+e^d\big)e^x+e^{2d}\big]}{(e^x-1)^3\big(e^d-e^x\big)^3}. \end{align*}

The three derivatives have a combined total of at most 5 zeroes in (0,d), and so Theorem 3·1 can indeed be applied with $m=5$ .

Unfortunately, the condition that A consists of a set of positive reals appears to be a more meaningful restriction for Corollary 4·2, and this cannot be easily removed by applying the result to a dilate of the set.

We have also directly verified that the additional condition of Theorem 3·1 is valid for other notable functions such as $f(x)=e^x$ and $f(x)=x^3$ . The details of these calculations are omitted. It appears likely that Theorem 3·1 also holds for $f(x)=x^d$ with $d \geq 3$ an integer. However, the additional condition does not hold for the quadratic function $f(x)=x^2$ .

We now use Corollary 4·2 to prove Theorem 1·2. We state and prove a more quantitatively precise version of the theorem below.

Corollary 4·3. Let A be a set of positive real numbers and suppose that $|AA| \leq K|A|$ . Then, for all $t \in \mathbb R$ such that $t \neq 0$ ,

\begin{equation*} |\{ (a,b) \in A \times A \,:\, a-b=t \}| \ll K^{\frac{405}{41}} |A|^{\frac{2}{3}- \frac{1}{123}} . \end{equation*}

Proof. Write

\begin{equation*}r_{A-A}(t)\,:\!=\, |\{ (a,b) \in A \times A \,:\, a-b=t \}|.\end{equation*}

Since $r_{A-A}(t)=r_{A-A}(-t)$ , we may assume without loss of generality that t is positive.

Denote $A(t)=A \cap (A-t)$ and observe that $|A(t)|=r_{A-A}(t)$ . Note also that $A(t), A(t)+t \subset A$ . Apply Corollary 4·2 with

\begin{equation*}X=A(t), \,\,\,\, \lambda=t.\end{equation*}

It follows that

\begin{equation*}\left|\frac{A^{(8)}}{A^{(7)}} \right | \geq \max \left \{\left|\frac{A(t)^{(8)}}{A(t)^{(7)}} \right |, \left|\frac{(A(t)+t)^{(5)}}{(A(t)+t)^{(4)}}\right| \right \} \gg |A(t)|^{\frac{3}{2}+ \frac{1}{54}}.\end{equation*}

However, using Theorem 2·3 in the multiplicative setting and the assumption that $|AA| \leq K|A|$ gives

\begin{equation*}|A(t)|^{\frac{3}{2}+ \frac{1}{54}} \ll K^{15}|A|.\end{equation*}

A rearrangement of this inequality completes the proof.

5. Proof of Theorem 1·1

In this section, we will prove Theorem 1·1. In fact, we will prove the following more general statement, from which Theorem 1·1 follows by setting $f(x) = \ln x$ . A concrete value for the constant c from Theorem 1·1 is given, namely $c= {1}/{162}$ , although the task of optimising this constant is not pursued to its fullest here.

Theorem 5·1. Let $a \in \mathbb R$ and let I denote the interval $I=(a, \infty)$ . Suppose that $A \subset I$ is a finite set. Suppose that $f\,:\,(a, \infty) \rightarrow \mathbb R$ is a strictly convex or concave function. Suppose also that, for any $d \in (0, \infty)$ , the function $f_d^{-1}\,:\, J \rightarrow I$ is 3-convex. Then

\begin{equation*} \max \{|16A|, |13f(A)| \} \gg |A|^{\frac{3}{2} +\frac{1}{162}}. \end{equation*}

Proof. An application of Theorem 2·2 with $k=8$ gives the bound

(15) \begin{equation} |8A| |8f(A)| \gg |A|^{3-\frac{1}{128}}.\end{equation}

It follows that we may assume that

(16) \begin{equation} |8A| \geq |A|^{\frac{3}{2} - \frac{1}{64}}.\end{equation}

Indeed, if (16) does not hold then (15) gives the bound $|8f(A)| \gg |A|^{\frac{3}{2} + \frac{1}{128}} $ , which is stronger than the result claimed in the statement of Theorem 5·1.

Two applications of Theorem 2·4 give the bounds

\begin{equation*}|8A-7A| \leq |8A-8A| \leq \frac{|8A+8A|^2}{|8A|} = \frac{|16A|^2}{|8A|}\end{equation*}

and similarly

\begin{equation*}|5f(A)-4f(A)| \leq \frac{|13f(A)|^2}{|8f(A)|}.\end{equation*}

Combining these bounds with (4), it follows that

\begin{equation*}\frac{|16A|^{32}}{|8A|^{16}} \cdot \frac{|13f(A)|^{22}}{|8f(A)|^{11}} \geq |8A-7A|^{16}|5f(A)-4f(A)|^{11} \gg |A|^{41}.\end{equation*}

Rearranging this inequality and then applying (15) yields

\begin{equation*}|16A|^{32}|13f(A)|^{22} \gg |A|^{41 } (|A|^{3-\frac{1}{128}})^{11} |8A|^5.\end{equation*}

Applying (16) and then tidying things up gives

\begin{equation*}|16A|^{32}|13f(A)|^{22} \gg |A|^{81 + \frac{1}{2}- \frac{21}{128}} \geq |A|^{81 + \frac{1}{3}}.\end{equation*}

Finally, the claimed bound follows from the pigeonhole principle.