Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Höhler, G.
1950.
Ferromagnetismus als Einstein‐Kondensation der Blochschen Spinwellen.
Annalen der Physik,
Vol. 442,
Issue. 1-2,
p.
93.
Fraser, A.R.
1951.
XIV. The condensation of a perfect Bose-Einstein gas.—I.
The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science,
Vol. 42,
Issue. 325,
p.
156.
Fraser, A.R.
1951.
XV. The condensation of a perfect Bose-Einstein gas.—II.
The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science,
Vol. 42,
Issue. 325,
p.
165.
Landsberg, P. T.
1954.
On Bose-Einstein Condensation.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 50,
Issue. 1,
p.
65.
Chester, G. V.
1954.
The Quantum-Mechanical Partition Function.
Physical Review,
Vol. 93,
Issue. 3,
p.
606.
Münster, Arnold
1956.
Statistische Thermodynamik.
p.
409.
Holthaus, Martin
and
Kalinowski, Eva
1999.
The Saddle-Point Method for Condensed Bose Gases.
Annals of Physics,
Vol. 276,
Issue. 2,
p.
321.
Kocharovsky, V. V.
Scully, Marlan O.
Zhu, Shi-Yao
and
Suhail Zubairy, M.
2000.
Condensation ofNbosons. II. Nonequilibrium analysis of an ideal Bose gas and the laser phase-transition analogy.
Physical Review A,
Vol. 61,
Issue. 2,
Kocharovsky, V. V.
Kocharovsky, Vl. V.
and
Scully, Marlan O.
2000.
Condensation ofNbosons. III. Analytical results for all higher moments of condensate fluctuations in interacting and ideal dilute Bose gases via the canonical ensemble quasiparticle formulation.
Physical Review A,
Vol. 61,
Issue. 5,
Xiong, Hongwei
Liu, Shujuan
Huang, Guoxiang
Xu, Zhijun
and
Zhang, Cunyuan
2001.
Fluctuations of the condensate in ideal and interacting Bose gases.
Journal of Physics B: Atomic, Molecular and Optical Physics,
Vol. 34,
Issue. 21,
p.
4203.
Xiong, Hongwei
Liu, Shujuan
Huang, Guoxiang
and
Xu, Zaixin
2002.
Canonical statistics of trapped ideal and interacting Bose gases.
Physical Review A,
Vol. 65,
Issue. 3,
Kocharovsky, Vitaly V.
Kocharovsky, Vladimir V.
Holthaus, Martin
Raymond Ooi, C.H.
Svidzinsky, Anatoly
Ketterle, Wolfgang
and
Scully, Marlan O.
2006.
Vol. 53,
Issue. ,
p.
291.
Kocharovsky, V. V.
Kocharovsky, Vl. V.
and
Dorfman, K. E.
2009.
Origin and universal structure of non-Gaussian statistics of Bose—Einstein condensate in a mesoscopic perfect gas.
Radiophysics and Quantum Electronics,
Vol. 52,
Issue. 5-6,
p.
422.
Kocharovsky, Vitaly V.
and
Kocharovsky, Vladimir V.
2010.
Analytical theory of mesoscopic Bose-Einstein condensation in an ideal gas.
Physical Review A,
Vol. 81,
Issue. 3,
Tarasov, S. V.
Kocharovsky, Vl. V.
and
Kocharovsky, V. V.
2014.
Universal scaling in the statistics and thermodynamics of a Bose-Einstein condensation of an ideal gas in an arbitrary trap.
Physical Review A,
Vol. 90,
Issue. 3,
Tarasov, S V
Kocharovsky, Vl V
and
Kocharovsky, V V
2014.
Universal fine structure of the specific heat at the criticalλ-point for an ideal Bose gas in an arbitrary trap.
Journal of Physics A: Mathematical and Theoretical,
Vol. 47,
Issue. 41,
p.
415003.
 for the mean occupation numbers is valid, whilst for temperatures rather lower than this critical value it will be shown that particles will condense into the lowest available state. The critical temperature T0 is given by
for the mean occupation numbers is valid, whilst for temperatures rather lower than this critical value it will be shown that particles will condense into the lowest available state. The critical temperature T0 is given by 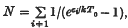 where the summation is over all energy levels except the lowest.
where the summation is over all energy levels except the lowest.