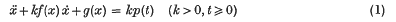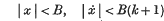Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Morris, G. R.
1955.
A differential equation for undamped forced non-linear oscillations. I.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 51,
Issue. 2,
p.
297.
Utz, W. R.
1956.
Boundedness and periodicity of solutions of the generalized liénard equation.
Annali di Matematica Pura ed Applicata,
Vol. 42,
Issue. 1,
p.
313.
Ezeilo, J. O. C.
1964.
On the existence of almost periodic solutions of some dissipative second order differential equations.
Annali di Matematica Pura ed Applicata,
Vol. 65,
Issue. 1,
p.
389.
SANSONE, G.
and
CONTI, R.
1964.
Non-Linear Differential Equations.
p.
359.
Putzer, Eugene J.
1964.
On Certain Systems of Nonlinear Differential Equations.
Journal of the Society for Industrial and Applied Mathematics,
Vol. 12,
Issue. 1,
p.
60.
Cartwright, M.L.
1972.
Ordinary Differential Equations.
p.
19.
Resatözkan, İ.
1981.
Total (practical) stability of ships.
Ocean Engineering,
Vol. 8,
Issue. 6,
p.
551.
Troesch, Albert
1982.
Theory and Applications of Singular Perturbations.
Vol. 942,
Issue. ,
p.
136.
Nakajima, Fumio
1994.
Ultimate boundedness of solutions for a generalized Liénard equation with forcing term.
Tohoku Mathematical Journal,
Vol. 46,
Issue. 3,
Bin, Liu
and
Jiangong, You
1994.
Quasiperiodic solutions for nonlinear differential equations of second order with symmetry.
Acta Mathematica Sinica,
Vol. 10,
Issue. 3,
p.
231.
Liu, Bin
and
Zanolin, Fabio
1998.
Boundedness of Solutions of Nonlinear Differential Equations.
Journal of Differential Equations,
Vol. 144,
Issue. 1,
p.
66.
Yuan, Rong
and
Yuan, Xiaoping
2001.
Boundedness of solutions for a class of nonlinear differential equations of second order via Moser's twist theorem.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 46,
Issue. 8,
p.
1073.
Piao, Daxiong
and
Li, Wenling
2008.
Boundedness of solutions for reversible system via Moser's twist theorem.
Journal of Mathematical Analysis and Applications,
Vol. 341,
Issue. 2,
p.
1224.
STEFANESCU, ION SABBA
2013.
THE ONSET OF BIFURCATIONS IN THE FORCED DUFFING EQUATION WITH DAMPING.
International Journal of Bifurcation and Chaos,
Vol. 23,
Issue. 02,
p.
1330006.
Pu, Zhi-Qiang
Yuan, Ru-Yi
Tan, Xiang-Min
and
Yi, Jian-Qiang
2014.
An Integrated Approach to Hypersonic Entry Attitude Control.
International Journal of Automation and Computing,
Vol. 11,
Issue. 1,
p.
39.
Chen, Lu
2023.
A KAM Theorem with Large Twist and Finite Smooth Large Perturbation.
Qualitative Theory of Dynamical Systems,
Vol. 22,
Issue. 3,