Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Keady, G.
and
Norbury, J.
1975.
Water waves and conjugate streams.
Journal of Fluid Mechanics,
Vol. 70,
Issue. 4,
p.
663.
Longuet-Higgins, M. S.
and
Fox, M. J. H.
1977.
Theory of the almost-highest wave: the inner solution.
Journal of Fluid Mechanics,
Vol. 80,
Issue. 4,
p.
721.
Keady, G.
and
Norbury, J.
1978.
On the existence theory for irrotational water waves.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 83,
Issue. 1,
p.
137.
Amick, C. J.
and
Toland, J. F.
1981.
On solitary water-waves of finite amplitude.
Archive for Rational Mechanics and Analysis,
Vol. 76,
Issue. 1,
p.
9.
1981.
On periodic water-waves and their convergence to solitary waves in the long-wave limit.
Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences,
Vol. 303,
Issue. 1481,
p.
633.
Amick, C. J.
1987.
Bounds for water waves.
Archive for Rational Mechanics and Analysis,
Vol. 99,
Issue. 2,
p.
91.
Craig, Walter
and
Sternberg, Peter
1988.
Symmetry of solitary waves.
Communications in Partial Differential Equations,
Vol. 13,
Issue. 5,
p.
603.
Craig, Walter
and
Sternberg, Peter
1992.
Symmetry of free-surface flows.
Archive for Rational Mechanics and Analysis,
Vol. 118,
Issue. 1,
p.
1.
Benjamin, T. Brooke
1995.
Verification of the Benjamin–Lighthill conjecture about steady water waves.
Journal of Fluid Mechanics,
Vol. 295,
Issue. -1,
p.
337.
Kozlov, V.
and
Kuznetsov, N.
2008.
On behaviour of free-surface profiles for bounded steady water waves.
Journal de Mathématiques Pures et Appliquées,
Vol. 90,
Issue. 1,
p.
1.
Matioc, Anca-Voichita
and
Matioc, Bogdan-Vasile
2012.
Regularity and symmetry properties of rotational solitary water waves.
Journal of Evolution Equations,
Vol. 12,
Issue. 2,
p.
481.
Geyer, Anna
2012.
Solitary Traveling Water Waves of Moderate Amplitude.
Journal of Nonlinear Mathematical Physics,
Vol. 19,
Issue. Supplement 1,
p.
104.
Stuhlmeier, Raphael
2012.
On Constant Vorticity Flows Beneath Two-Dimensional Surface Solitary Waves.
Journal of Nonlinear Mathematical Physics,
Vol. 19,
Issue. Supplement 1,
p.
34.
Kozlov, Vladimir
and
Kuznetsov, Nikolay
2012.
Bounds for steady water waves with vorticity.
Journal of Differential Equations,
Vol. 252,
Issue. 1,
p.
663.
Wheeler, Miles H.
2015.
The Froude number for solitary water waves with vorticity.
Journal of Fluid Mechanics,
Vol. 768,
Issue. ,
p.
91.
Chen, Robin Ming
Walsh, Samuel
and
Wheeler, Miles H.
2016.
On the existence and qualitative theory of stratified solitary water waves.
Comptes Rendus. Mathématique,
Vol. 354,
Issue. 6,
p.
601.
Wheeler, Miles H.
2018.
Integral and Asymptotic Properties of Solitary Waves in Deep Water.
Communications on Pure and Applied Mathematics,
Vol. 71,
Issue. 10,
p.
1941.
Walsh, Samuel
Wheeler, Miles H.
and
Chen, Robin Ming
2018.
Existence and qualitative theory for stratified solitary water waves.
Annales de l'Institut Henri Poincaré C, Analyse non linéaire,
Vol. 35,
Issue. 2,
p.
517.
Kozlov, Vladimir
Lokharu, Evgeniy
and
Wheeler, Miles H.
2021.
Nonexistence of Subcritical Solitary Waves.
Archive for Rational Mechanics and Analysis,
Vol. 241,
Issue. 1,
p.
535.
Lokharu, Evgeniy
2021.
On bounds for steady waves with negative vorticity.
Journal of Mathematical Fluid Mechanics,
Vol. 23,
Issue. 2,
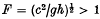 , where c is the speed of the stream, h is its depth, and g is the gravity constant).
, where c is the speed of the stream, h is its depth, and g is the gravity constant).