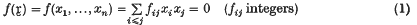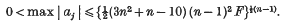Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Davenport, H.
1956.
Indefinite quadratic forms in many variables.
Mathematika,
Vol. 3,
Issue. 2,
p.
81.
Davenport, H.
1957.
Note on a theorem of cassels.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 53,
Issue. 2,
p.
539.
Watson, G. L.
1957.
Least solutions of homogeneous quadratic equations.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 53,
Issue. 2,
p.
541.
Birch, B. J.
and
Davenport, H.
1958.
On a theorem of Davenport, and Heilbronn.
Acta Mathematica,
Vol. 100,
Issue. 3-4,
p.
259.
Lawton, B.
1958.
Bounded representations of the positive values of an indefinite quadratic form.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 54,
Issue. 1,
p.
14.
Birch, B. J.
and
Davenport, H.
1958.
Quadratic equations in several variables.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 54,
Issue. 2,
p.
135.
Birch, B. J.
and
Davenport, H.
1958.
Indefinite quadratic forms in many variables.
Mathematika,
Vol. 5,
Issue. 1,
p.
8.
1969.
Geometry of Numbers.
p.
471.
1969.
Vol. 30,
Issue. ,
p.
42.
Halberstam, H.
and
Burgess, D. A.
1971.
Harold Davenport, 1907-1969.
Biographical Memoirs of Fellows of the Royal Society,
Vol. 17,
Issue. ,
p.
159.
Davenport, H.
1971.
Homogeneous quadratic equations.
Mathematika,
Vol. 18,
Issue. 1,
p.
1.
Malyshev, A. V.
and
Podsypanin, E. V.
1976.
Analytic methods in the theory of systems of diophantine equations and inequalities with a large number of unknowns.
Journal of Soviet Mathematics,
Vol. 5,
Issue. 6,
p.
753.
Garbanati, Dennis A.
1978.
An algorithm for the representation of zero by a quadratic form.
Journal of Pure and Applied Algebra,
Vol. 13,
Issue. 1,
p.
57.
Siegel, Carl Ludwig
Chandrasekharan, K.
and
Maaß, H.
1979.
Gesammelte Abhandlungen.
p.
250.
Baker, R. C.
1980.
Small solutions of quadratic and quartic congruences.
Mathematika,
Vol. 27,
Issue. 1,
p.
30.
Chalk, J. H. H.
1980.
Linearly independent zeros of quadratic forms over number-fields.
Monatshefte für Mathematik,
Vol. 90,
Issue. 1,
p.
13.
Schulze-Pillot, Rainer
1983.
Small linearly independent zeros of quadratic forms.
Monatshefte f�r Mathematik,
Vol. 95,
Issue. 3,
p.
241.
Schlickewei, Hans Peter
1985.
Kleine Nullstellen homogener quadratischer Gleichungen.
Monatshefte f�r Mathematik,
Vol. 100,
Issue. 1,
p.
35.
Frumkin, M. A.
1985.
Complexity questions in number theory.
Journal of Soviet Mathematics,
Vol. 29,
Issue. 4,
p.
1502.
Schmidt, Wolfgang M.
1985.
Small zeros of quadratic forms.
Transactions of the American Mathematical Society,
Vol. 291,
Issue. 1,
p.
87.