Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Urabe, Tohsuke
1996.
Calculation of Manin’s invariant for Del Pezzo surfaces.
Mathematics of Computation,
Vol. 65,
Issue. 213,
p.
247.
Colliot-Thélène, Jean-Louis
and
Poonen, Bjorn
1999.
Algebraic families of nonzero elements of Shafarevich-Tate groups.
Journal of the American Mathematical Society,
Vol. 13,
Issue. 1,
p.
83.
Yanchevskii, V.
Margolin, G.
and
Rehmann, U.
2000.
Brauer groups of curves and unramified, central simple algebras over their function fields.
Journal of Mathematical Sciences,
Vol. 102,
Issue. 3,
p.
4071.
Poonen, Bjorn
and
Voloch, José Felipe
2004.
Arithmetic of Higher-Dimensional Algebraic Varieties.
Vol. 226,
Issue. ,
p.
175.
Bright, M.J.
Bruin, N.
Flynn, E.V
and
Logan, A.
2007.
The Brauer-Manin Obstruction and III[2].
LMS Journal of Computation and Mathematics,
Vol. 10,
Issue. ,
p.
354.
Bright, Martin
2011.
Evaluating Azumaya algebras on cubic surfaces.
Manuscripta Mathematica,
Vol. 134,
Issue. 3-4,
p.
405.
ELSENHANS, ANDREAS-STEPHAN
and
JAHNEL, JÖRG
2011.
CUBIC SURFACES WITH A GALOIS INVARIANT PAIR OF STEINER TRIHEDRA.
International Journal of Number Theory,
Vol. 07,
Issue. 04,
p.
947.
CARTER, ANDREA C.
2011.
THE BRAUER GROUP OF DEL PEZZO SURFACES.
International Journal of Number Theory,
Vol. 07,
Issue. 02,
p.
261.
Siksek, Samir
2012.
On the number of Mordell–Weil generators for cubic surfaces.
Journal of Number Theory,
Vol. 132,
Issue. 11,
p.
2610.
Hassett, Brendan
and
Várilly-Alvarado, Anthony
2013.
Failure of the Hasse principle on general surfaces.
Journal of the Institute of Mathematics of Jussieu,
Vol. 12,
Issue. 4,
p.
853.
Várilly-Alvarado, Anthony
2013.
Birational Geometry, Rational Curves, and Arithmetic.
p.
293.
Várilly-Alvarado, Anthony
and
Viray, Bianca
2014.
Arithmetic of del Pezzo surfaces of degree 4 and vertical Brauer groups.
Advances in Mathematics,
Vol. 255,
Issue. ,
p.
153.
Bright, Martin
2015.
Bad reduction of the Brauer-Manin obstruction.
Journal of the London Mathematical Society,
Vol. 91,
Issue. 3,
p.
643.
Jahnel, Jörg
and
Schindler, Damaris
2017.
On integral points on degree four del Pezzo surfaces.
Israel Journal of Mathematics,
Vol. 222,
Issue. 1,
p.
21.
Browning, T. D.
2017.
MANY CUBIC SURFACES CONTAIN RATIONAL POINTS.
Mathematika,
Vol. 63,
Issue. 3,
p.
818.
Liedtke, Christian
2017.
Geometry Over Nonclosed Fields.
p.
157.
Cantoral‐Farfán, Victoria
Tang, Yunqing
Tanimoto, Sho
and
Visse, Erik
2018.
Effective bounds for Brauer groups of Kummer surfaces over number fields.
Journal of the London Mathematical Society,
Vol. 97,
Issue. 3,
p.
353.
West, Mckenzie
2018.
Women in Numbers Europe II.
Vol. 11,
Issue. ,
p.
199.
Creutz, Brendan
and
Viray, Bianca
2018.
Degree and the Brauer–Manin
obstruction.
Algebra & Number Theory,
Vol. 12,
Issue. 10,
p.
2445.
Auel, Asher
Böhning, Christian
and
Pirutka, Alena
2018.
Stable rationality of quadric and cubic surface bundle fourfolds.
European Journal of Mathematics,
Vol. 4,
Issue. 3,
p.
732.
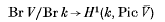
 .
.