No CrossRef data available.
Carleman's formula for subharmonic functions
Published online by Cambridge University Press: 24 October 2008
Extract
The purpose of this paper is to prove theorems for subharmonic functions analogous to those stated below for regular functions. We make the following definition: D(∈, R) is the domain in the Euclidean plane defined by
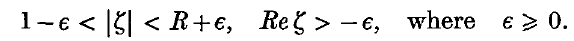
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 62 , Issue 1 , January 1966 , pp. 51 - 60
- Copyright
- Copyright © Cambridge Philosophical Society 1966


