Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Campbell, C. M.
Conder, M. D. E.
and
Robertson, E. F.
1994.
Defining-relations for Hurwitz groups.
Glasgow Mathematical Journal,
Vol. 36,
Issue. 3,
p.
363.
Howie, J.
Metaftsis, V.
and
Thomas, R. M.
1995.
Finite generalized triangle groups.
Transactions of the American Mathematical Society,
Vol. 347,
Issue. 9,
p.
3613.
Винберг, Эрнест Борисович
and
Vinberg, Ernest Borisovich
1997.
Группы, задаваемые периодическими попарными соотношениями.
Математический сборник,
Vol. 188,
Issue. 9,
p.
3.
Vinberg, E B
1997.
Groups defined by periodic paired relations.
Sbornik: Mathematics,
Vol. 188,
Issue. 9,
p.
1269.
Howie, J.
1998.
Free subgroups in groups of small deficiency.
Journal of Group Theory,
Vol. 1,
Issue. 1,
BUTTON, J. O.
and
THILLAISUNDARAM, A.
2011.
APPLICATIONS OF p-DEFICIENCY AND p-LARGENESS.
International Journal of Algebra and Computation,
Vol. 21,
Issue. 04,
p.
547.
Chatterji, Indira
Hughes, Sam
and
Kropholler, Peter
2021.
The first -betti number and groups acting on trees.
Proceedings of the Edinburgh Mathematical Society,
Vol. 64,
Issue. 4,
p.
916.


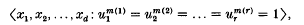
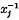 , and suppose that there is a homomorphism σ such that the orders of the elements
, and suppose that there is a homomorphism σ such that the orders of the elements 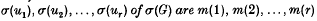 respectively. Let
respectively. Let 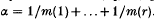 If G is finite, then α−d + 1 > 0 and
If G is finite, then α−d + 1 > 0 and 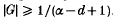 .
.