Article contents
Chaos map for the universal enveloping algebra of U(N)*
Published online by Cambridge University Press: 24 October 2008
Abstract
It is shown that the family of representations {jt, t ∈ ℝ+} of the universal enveloping algebra U of the N-dimensional unitary group which is generated by the N-dimensional number process of quantum stochastic calculus can be expressed in the form
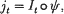
where ψ is a bijective linear map from U onto the space S of symmetric tensors over the Lie algebra, and It is the iterated (chaotic) integral on S. The chaotic product * is defined by the formula
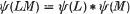
and satisfies

This work generalizes and completes earlier results on the centre of U.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 117 , Issue 1 , January 1995 , pp. 21 - 30
- Copyright
- Copyright © Cambridge Philosophical Society 1995
References
REFERENCES
- 6
- Cited by


