Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Gregory, R. D.
1979.
The edge-cracked circular disc under symmetric pin-loading.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 85,
Issue. 3,
p.
523.
Gregory, R. D.
1980.
The traction boundary value problem for the elastostatic semi-infinite strip; existence of solution, and completeness of the Papkovich-Fadle eigenfunctions.
Journal of Elasticity,
Vol. 10,
Issue. 3,
p.
295.
Bilby, B. A.
1980.
Tewksbury Lecture: Putting fracture to work.
Journal of Materials Science,
Vol. 15,
Issue. 3,
p.
535.
Kendall, K.
and
Gregory, R. D.
1987.
Fracture of radially edge-cracked discs.
Journal of Materials Science,
Vol. 22,
Issue. 12,
p.
4514.
Gregory, R. D.
1989.
The spinning circular disc with a radial edge crack; an exact solution.
International Journal of Fracture,
Vol. 41,
Issue. 1,
p.
39.
Orynyak, I. V.
1990.
Constructing the weight function for flat solids with cracks.
Strength of Materials,
Vol. 22,
Issue. 8,
p.
1117.
Wu, X. R.
1991.
The arbitrarily loaded single-edge cracked circular disc; accurate weight function solutions.
International Journal of Fracture,
Vol. 49,
Issue. 4,
p.
239.
Schneider, G. A.
Magerl, F.
Hahn, I.
and
Petzow, G.
1993.
Thermal Shock and Thermal Fatigue Behavior of Advanced Ceramics.
p.
229.
Schneider, G. A.
1994.
Tailoring of Mechanical Properties of Si3N4 Ceramics.
p.
379.
Schneider, G.A.
Magerl, F.
and
Petzow, G.
1994.
Superconductors, Surfaces and Superlattices.
p.
837.
SCHINDLER, H.J.
1994.
Advances in Fracture Resistance and Structural Integrity.
p.
193.
Schneider, G.A.
and
Nickel, K.G.
1994.
Corrosion of Advanced Ceramics.
Vol. 267,
Issue. ,
p.
375.
Magerl, F.
Schneider, G.A.
and
Petzow, G.
1994.
Advanced Materials '93.
p.
395.
Schindler, H. J.
1996.
Determination of residual stress distributions from measured stress intensity factors.
International Journal of Fracture,
Vol. 74,
Issue. 2,
p.
R23.
Ma, C.-C.
and
Liao, M.-H.
1996.
Analysis of Axial Cracks in Hollow Cylinders Subjected to Thermal Shock by Using the Thermal Weight Function Method.
Journal of Pressure Vessel Technology,
Vol. 118,
Issue. 2,
p.
146.
Schindler, H. -J.
Cheng, W.
and
Finnie, I.
1997.
Experimental determination of stress intensity factors due to residual stresses.
Experimental Mechanics,
Vol. 37,
Issue. 3,
p.
272.
Ciavarella, M
Demelio, G
and
Pappalettere, C
1998.
On the post-processing of data obtained from cracked components.
The Journal of Strain Analysis for Engineering Design,
Vol. 33,
Issue. 1,
p.
67.
Orynyak, I. V.
Borodii, M. V.
and
Krasovs'kyi, A. Ya
1998.
A method for the evaluation of the stress intensity factors for cracks originating from notches.
Materials Science,
Vol. 34,
Issue. 5,
p.
672.
Schindler, H-J
1999.
Advances in Fatigue Crack Closure Measurement and Analysis: Second Volume.
p.
175.
Kendall, Kevin
2002.
Adhesion Science and Engineering.
p.
77.
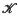 at the crack tip, the total strain energy W, and the opening U at the mouth of the crack, are given exactly by
at the crack tip, the total strain energy W, and the opening U at the mouth of the crack, are given exactly by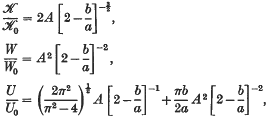
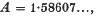
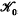 , W0, U0 are normalising factors defined in section 6.
, W0, U0 are normalising factors defined in section 6.

