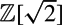 $\mathbb{Z}[\sqrt{2}]$
$\mathbb{Z}[\sqrt{2}]$Published online by Cambridge University Press: 09 December 2016
There are 432 strongly squarefree symmetric bilinear forms of signature (2, 1) defined over 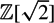 $\mathbb{Z}[\sqrt{2}]$ whose integral isometry groups are generated up to finite index by finitely many reflections. We adapted Allcock's method (based on Nikulin's) of analysis for the 2-dimensional Weyl chamber to the real quadratic setting, and used it to produce a finite list of quadratic forms which contains all of the ones of interest to us as a sub-list. The standard method for determining whether a hyperbolic reflection group is generated up to finite index by reflections is an algorithm of Vinberg. However, for a large number of our quadratic forms the computation time required by Vinberg's algorithm was too long. We invented some alternatives, which we present here.
$\mathbb{Z}[\sqrt{2}]$ whose integral isometry groups are generated up to finite index by finitely many reflections. We adapted Allcock's method (based on Nikulin's) of analysis for the 2-dimensional Weyl chamber to the real quadratic setting, and used it to produce a finite list of quadratic forms which contains all of the ones of interest to us as a sub-list. The standard method for determining whether a hyperbolic reflection group is generated up to finite index by reflections is an algorithm of Vinberg. However, for a large number of our quadratic forms the computation time required by Vinberg's algorithm was too long. We invented some alternatives, which we present here.