Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Martin Edwards, C.
and
R�ttimann, Gottfried T.
1995.
Lattice of tripotents in a JBW*-triple.
International Journal of Theoretical Physics,
Vol. 34,
Issue. 8,
p.
1349.
Maitland Wright, J. D.
1998.
Sesquilinear forms on Jordan triple systems.
Rendiconti del Circolo Matematico di Palermo,
Vol. 47,
Issue. 3,
p.
465.
Edwards, C.Martin
Lörch, Daniel
and
Rüttimann, Gottfried T.
1999.
Compatible Subtriples of Jordan-Triples.
Journal of Algebra,
Vol. 216,
Issue. 2,
p.
707.
Edwards, C. Martin
and
Rüttimann, Gottfried T.
2003.
Faithful Inner Ideals in Jbw*-Triples.
Results in Mathematics,
Vol. 43,
Issue. 3-4,
p.
245.
Burgos, María
Fernández-Polo, Francisco J.
Garcés, Jorge J.
Moreno, Juan Martínez
and
Peralta, Antonio M.
2008.
Orthogonality preservers in C∗-algebras, JB∗-algebras and JB∗-triples.
Journal of Mathematical Analysis and Applications,
Vol. 348,
Issue. 1,
p.
220.
Altwaijry, Najla A.
and
Edwards, C. Martin
2008.
The Banach–Lie algebra of multiplication operators on a JBW∗-triple.
Journal of Functional Analysis,
Vol. 254,
Issue. 11,
p.
2866.
Lubbe, Andreas A.
2009.
INVOLUTIVE GRADINGS AND KERNELS IN JBW*-TRIPLES.
Asian-European Journal of Mathematics,
Vol. 02,
Issue. 03,
p.
453.
Burgos, María
Fernández-Polo, Francisco J.
Garcés, Jorge J.
and
Peralta, Antonio M.
2009.
ORTHOGONALITY PRESERVERS REVISITED.
Asian-European Journal of Mathematics,
Vol. 02,
Issue. 03,
p.
387.
Edwards, C. Martin
Fernández-Polo, Francisco J.
Hoskin, Christopher S.
and
Peralta, Antonio M.
2010.
On the facial structure of the unit ball in a JB*-triple.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2010,
Issue. 641,
Fernández-Polo, Francisco J.
and
Peralta, Antonio M.
2010.
Non-commutative generalisations of Urysohn's lemma and hereditary inner ideals.
Journal of Functional Analysis,
Vol. 259,
Issue. 2,
p.
343.
Fernández-Polo, Francisco J.
and
Peralta, Antonio M.
2010.
On the facial structure of the unit ball in the dual space of a JB*-triple.
Mathematische Annalen,
Vol. 348,
Issue. 4,
p.
1019.
Blecher, David P.
and
Read, Charles John
2011.
Operator algebras with contractive approximate identities.
Journal of Functional Analysis,
Vol. 261,
Issue. 1,
p.
188.
Fernández-Polo, Francisco J.
Garcés, Jorge J.
and
Peralta, Antonio M.
2012.
Weakly compact orthogonality preservers on C*-algebras.
Mathematische Zeitschrift,
Vol. 270,
Issue. 3-4,
p.
709.
Lubbe, Andreas A.
2012.
Complementary inner ideals in JBW⁎-triples.
Journal of Algebra,
Vol. 350,
Issue. 1,
p.
36.
Tahlawi, Haifa M.
Siddiqui, Akhlaq A.
and
Jamjoom, Fatmah B.
2013.
On the Geometry of the Unit Ball of aJB*-Triple.
Abstract and Applied Analysis,
Vol. 2013,
Issue. ,
p.
1.
Burgos, Maria
Fernández-Polo, Francisco J.
and
Peralta, Antonio M.
2014.
Local triple derivations on C∗-algebras and JB∗-triples.
Bulletin of the London Mathematical Society,
Vol. 46,
Issue. 4,
p.
709.
Edwards, C. Martin
and
Oliveira, Lina
2015.
Local facial structure and norm-exposed faces of the unit ball in a JB⁎-triple.
Journal of Mathematical Analysis and Applications,
Vol. 421,
Issue. 2,
p.
1315.
Burgos, María J.
Cabello, Juan Carlos
and
Peralta, Antonio M.
2016.
Weak-local triple derivations on C⁎-algebras and JB⁎-triples.
Linear Algebra and its Applications,
Vol. 506,
Issue. ,
p.
614.
Blecher, David
and
Neal, Matthew
2016.
Completely contractive projections on operator algebras.
Pacific Journal of Mathematics,
Vol. 283,
Issue. 2,
p.
289.
Peralta, Antonio M.
and
Pfitzner, Hermann
2016.
Perturbation of ℓ1-copies in preduals of JBW⁎-triples.
Journal of Mathematical Analysis and Applications,
Vol. 434,
Issue. 1,
p.
149.
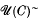 consisting of the partially ordered set
consisting of the partially ordered set 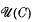 of tripotents in a JBW*-triple C with a greatest element adjoined forms a complete lattice. This paper is mainly concerned with the situation in which C is the second dual A** of a complex Banach space A and, more particularly, when A is itself a JB*-triple. A subset
of tripotents in a JBW*-triple C with a greatest element adjoined forms a complete lattice. This paper is mainly concerned with the situation in which C is the second dual A** of a complex Banach space A and, more particularly, when A is itself a JB*-triple. A subset 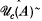 of
of 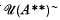 consisting of the set
consisting of the set 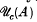 of tripotents compact relative to A (denned in Section 4) with a greatest element adjoined is studied. It is shown to be an atomic complete lattice with the properties that the infimum of an arbitrary family of elements of
of tripotents compact relative to A (denned in Section 4) with a greatest element adjoined is studied. It is shown to be an atomic complete lattice with the properties that the infimum of an arbitrary family of elements of 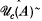 is the same whether taken in
is the same whether taken in 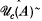 or in
or in 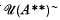 and that every decreasing net of non-zero elements of
and that every decreasing net of non-zero elements of 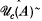 has a non-zero infimum. The relationship between the complete lattice
has a non-zero infimum. The relationship between the complete lattice 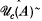 and the complete lattice
and the complete lattice 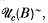 where B is a Banach space such that B** is a weak*-closed subtriple of A** is also investigated. When applied to the special case in which A is a C*-algebra the results provide information about the set of compact partial isometries relative to A and are closely related to those recently obtained by Akemann and Pedersen. In particular it is shown that a partial isometry is compact relative to A if and only if, in their terminology, it belongs locally to A. The main results are applied to this and other examples.
where B is a Banach space such that B** is a weak*-closed subtriple of A** is also investigated. When applied to the special case in which A is a C*-algebra the results provide information about the set of compact partial isometries relative to A and are closely related to those recently obtained by Akemann and Pedersen. In particular it is shown that a partial isometry is compact relative to A if and only if, in their terminology, it belongs locally to A. The main results are applied to this and other examples.

