Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Vignati, Marco
1987.
Complex interpolation and convexity.
Proceedings of the American Mathematical Society,
Vol. 99,
Issue. 4,
p.
705.
Xu, Quanhua
1987.
Geometrical Aspects of Functional Analysis.
Vol. 1267,
Issue. ,
p.
210.
Lešnjak, Gorazd
1988.
Complex convexity and finitely additive vector measures.
Proceedings of the American Mathematical Society,
Vol. 102,
Issue. 4,
p.
867.
Xu, Quanhua
1991.
Analytic functions with values in lattices and symmetric spaces of measurable operators.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 109,
Issue. 3,
p.
541.
Dineen, Seán
and
Timoney, Richard M.
1992.
Progress in Functional Analysis, Proceedings of the International Functional Analysis Meeting on the Occasion of the 60th Birthday of Professor M. Valdivia.
Vol. 170,
Issue. ,
p.
333.
Mupasiri, Douglas
1995.
Complex extreme measurable selections.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 58,
Issue. 2,
p.
222.
Dowling, Patrick
Hu, Zhibao
and
Mupasiri, Douglas
1996.
Complex convexity in Lebesgue-Bochner Function Spaces.
Transactions of the American Mathematical Society,
Vol. 348,
Issue. 1,
p.
127.
Defant, Andreas
Mastyło, Mieczysław
and
Michels, Carsten
2002.
Orlicz norm estimates for eigenvalues of matrices.
Israel Journal of Mathematics,
Vol. 132,
Issue. 1,
p.
45.
Lee, Han Ju
2005.
Monotonicity and complex convexity in Banach lattices.
Journal of Mathematical Analysis and Applications,
Vol. 307,
Issue. 1,
p.
86.
Dowling, Patrick N.
and
Turett, Barry
2006.
Complex strict convexity of absolute norms on Cn and direct sums of Banach spaces.
Journal of Mathematical Analysis and Applications,
Vol. 323,
Issue. 2,
p.
930.
Lee, Han Ju
2007.
Complex convexity and monotonicity in quasi-Banach lattices.
Israel Journal of Mathematics,
Vol. 159,
Issue. 1,
p.
57.
Chen, Lili
Cui, Yunan
and
Hudzik, Henryk
2009.
Criteria for complex strongly extreme points of Musielak–Orlicz function spaces.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 70,
Issue. 6,
p.
2270.
Lee, Han Ju
2010.
RANDOMIZED SERIES AND GEOMETRY OF BANACH SPACES.
Taiwanese Journal of Mathematics,
Vol. 14,
Issue. 5,
Czerwińska, M. M.
and
Parrish, A.
2015.
Complex extreme points in Marcinkiewicz spaces.
Positivity,
Vol. 19,
Issue. 1,
p.
121.
Kim, Sun Kwang
Lee, Han Ju
and
Martín, Miguel
2016.
Bishop–Phelps–Bollobás property for bilinear forms on spaces of continuous functions.
Mathematische Zeitschrift,
Vol. 283,
Issue. 1-2,
p.
157.
Blasco, O.
2017.
The p-Bohr radius of a Banach space.
Collectanea Mathematica,
Vol. 68,
Issue. 1,
p.
87.
Allu, Vasudevarao
Halder, Himadri
and
Pal, Subhadip
2023.
Bohr and Rogosinski inequalities for operator valued holomorphic functions.
Bulletin des Sciences Mathématiques,
Vol. 182,
Issue. ,
p.
103214.
Jenkins, Jonathan
and
Tkocz, Tomasz
2024.
Complex Hanner’s inequality for many functions.
Israel Journal of Mathematics,
Vol. 262,
Issue. 1,
p.
475.
Wilke, Anne-Edgar
2024.
Convexity, plurisubharmonicity and the strong maximum modulus principle in Banach spaces.
Confluentes Mathematici,
Vol. 15,
Issue. ,
p.
83.
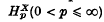 and makes a comparison with the more familiar modulus of uniform convexity. It is shown that unconditional convergence of
and makes a comparison with the more familiar modulus of uniform convexity. It is shown that unconditional convergence of 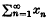 implies convergence of
implies convergence of 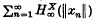 . In the next section the moduli
. In the next section the moduli 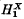 and
and 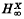 are shown to be related. The method of proof gives rise to a theorem about strict c-convexity of Lp(X) and a result on the representability
are shown to be related. The method of proof gives rise to a theorem about strict c-convexity of Lp(X) and a result on the representability 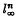 in Lp(X).
in Lp(X).

