Article contents
Computing nilpotent and unipotent canonical forms: a symmetric approach
Published online by Cambridge University Press: 19 October 2011
Abstract
Let k be an algebraically closed field of any characteristic except 2, and let G = GLn(k) be the general linear group, regarded as an algebraic group over k. Using an algebro-geometric argument and Dynkin–Kostant theory for G we begin by obtaining a canonical form for nilpotent Ad(G)-orbits in 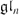 (k) which is symmetric with respect to the non-main diagonal (i.e. it is fixed by the map f : (xi,j) ↦ (xn+1−j,n+1−i)), with entries in {0,1}. We then show how to modify this form slightly in order to satisfy a non-degenerate symmetric or skew-symmetric bilinear form, assuming that the orbit does not vanish in the presence of such a form. Replacing G by any simple classical algebraic group we thus obtain a unified approach to computing representatives for nilpotent orbits of all classical Lie algebras. By applying Springer morphisms, this also yields representatives for the corresponding unipotent classes in G. As a corollary we obtain a complete set of generic canonical representatives for the unipotent classes in finite general unitary groups GUn(
(k) which is symmetric with respect to the non-main diagonal (i.e. it is fixed by the map f : (xi,j) ↦ (xn+1−j,n+1−i)), with entries in {0,1}. We then show how to modify this form slightly in order to satisfy a non-degenerate symmetric or skew-symmetric bilinear form, assuming that the orbit does not vanish in the presence of such a form. Replacing G by any simple classical algebraic group we thus obtain a unified approach to computing representatives for nilpotent orbits of all classical Lie algebras. By applying Springer morphisms, this also yields representatives for the corresponding unipotent classes in G. As a corollary we obtain a complete set of generic canonical representatives for the unipotent classes in finite general unitary groups GUn(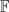 q) for all prime powers q.
q) for all prime powers q.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 152 , Issue 1 , January 2012 , pp. 35 - 53
- Copyright
- Copyright © Cambridge Philosophical Society 2011
References
REFERENCES
- 2
- Cited by


