Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Rosebrugh, Robert
and
Wood, R. J.
1991.
Constructive complete distributivity II.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 110,
Issue. 2,
p.
245.
Vickers, Steven
1993.
Information systems for continuous posets.
Theoretical Computer Science,
Vol. 114,
Issue. 2,
p.
201.
Rosebrugh, Robert
and
Wood, R. J.
1994.
Constructive complete distributivity IV.
Applied Categorical Structures,
Vol. 2,
Issue. 2,
p.
119.
Rosebrugh, Robert
and
Wood, R. J.
1994.
An adjoint characterization of the category of sets.
Proceedings of the American Mathematical Society,
Vol. 122,
Issue. 2,
p.
409.
Marmolejo, F.
Rosebrugh, R.D.
and
Wood, R.J.
2002.
A basic distributive law.
Journal of Pure and Applied Algebra,
Vol. 168,
Issue. 2-3,
p.
209.
Butz, Carsten
2004.
Saturated models of intuitionistic theories.
Annals of Pure and Applied Logic,
Vol. 129,
Issue. 1-3,
p.
245.
Stubbe, Isar
2006.
Towards “Dynamic Domains”: Totally Continuous Cocomplete Q-categories.
Electronic Notes in Theoretical Computer Science,
Vol. 155,
Issue. ,
p.
617.
Stubbe, Isar
2007.
Towards “dynamic domains”: Totally continuous cocomplete Q-categories.
Theoretical Computer Science,
Vol. 373,
Issue. 1-2,
p.
142.
Kenney, Toby
2010.
The General Theory of Diads.
Applied Categorical Structures,
Vol. 18,
Issue. 5,
p.
523.
Lucyshyn-Wright, Rory B.B.
2012.
Totally distributive toposes.
Journal of Pure and Applied Algebra,
Vol. 216,
Issue. 11,
p.
2425.
Hofmann, Dirk
and
Waszkiewicz, Paweł
2012.
A duality of quantale-enriched categories.
Journal of Pure and Applied Algebra,
Vol. 216,
Issue. 8-9,
p.
1866.
Hofmann, Dirk
2013.
A Four for the Price of One Duality Principle for Distributive Spaces.
Order,
Vol. 30,
Issue. 2,
p.
643.
Ghani, Neil
Johann, Patricia
Forsberg, Fredrik Nordvall
Orsanigo, Federico
and
Revell, Tim
2015.
Bifibrational Functorial Semantics of Parametric Polymorphism.
Electronic Notes in Theoretical Computer Science,
Vol. 319,
Issue. ,
p.
165.
Babus, Octavian
and
Kurz, Alexander
2016.
Coalgebraic Methods in Computer Science.
Vol. 9608,
Issue. ,
p.
136.
Clementino, Maria Manuel
and
Hofmann, Dirk
2017.
The rise and fall of V-functors.
Fuzzy Sets and Systems,
Vol. 321,
Issue. ,
p.
29.
Hofmann, Dirk
and
Nora, Pedro
2020.
Hausdorff Coalgebras.
Applied Categorical Structures,
Vol. 28,
Issue. 5,
p.
773.
Townsend, Christopher
2022.
Stably locally compact locales are dual to continuous posets.
Journal of Pure and Applied Algebra,
Vol. 226,
Issue. 2,
p.
106836.
MANUELL, GRAHAM
2022.
The spectrum of a localic semiring.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 173,
Issue. 3,
p.
647.
Lieberman, Michael
Rosický, Jiří
and
Zambrano, Pedro
2023.
Tameness in generalized metric structures.
Archive for Mathematical Logic,
Vol. 62,
Issue. 3-4,
p.
531.
Clementino, Maria Manuel
Fitas, Carlos
and
Hofmann, Dirk
2025.
A variety of co-quasivarieties.
Topology and its Applications,
p.
109226.
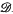 L a class of subsets of L, and suppose that L has a supremum for each element in
L a class of subsets of L, and suppose that L has a supremum for each element in 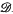 L. We might say that L has
L. We might say that L has 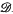 -sups. The ‘distributivity’ we refer to is that of infs over
-sups. The ‘distributivity’ we refer to is that of infs over 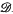 -sups. The ‘adjunction’ is that given by a left adjoint to the map V:
-sups. The ‘adjunction’ is that given by a left adjoint to the map V: 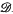 L→L. Now the latter has a left adjoint if and only if it preserves infs, and this means roughly that the
L→L. Now the latter has a left adjoint if and only if it preserves infs, and this means roughly that the 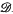 -sup of an intersection is an inf of
-sup of an intersection is an inf of 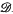 -sups. When one does succeed in identifying the
-sups. When one does succeed in identifying the 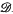 -sup of an intersection as a
-sup of an intersection as a 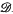 -sup of infs, one has an instance of distributivity.
-sup of infs, one has an instance of distributivity.

