Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Casazza, P. G.
and
Jarchow, H.
1996.
Self-induced compactness in Banach spaces.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 126,
Issue. 2,
p.
355.
Runde, Volker
2000.
Automatic continuity and second order cohomology.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 68,
Issue. 2,
p.
231.
García, M. Cabrera
Dales, H. G.
and
Palacios, Á. Rodríguez
2020.
Maximal left ideals in Banach algebras.
Bulletin of the London Mathematical Society,
Vol. 52,
Issue. 1,
p.
1.


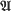 be a Banach algebra. We say that homomorphisms from
be a Banach algebra. We say that homomorphisms from 