Hostname: page-component-6bf8c574d5-8gtf8 Total loading time: 0 Render date: 2025-02-24T06:41:14.107Z Has data issue: false hasContentIssue false
  • English
  • Français

Contributions to the theory of Ramanujan's function τ(n) and similar arithmetical functions

I. The zeros of the function on the line

Published online by Cambridge University Press:  24 October 2008

R. A. Rankin
R. A. Rankin
Affiliation:
Clare CollegeCambridge
Get access Rights & Permissions [Opens in a new window]

Extract

In this and the succeeding paper I solve two problems suggested by Prof. Hardy, namely (1) that of proving that Ramanujan's function

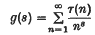
has no zeros on the line 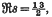and (2) that of finding an asymptotic formula

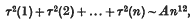
where A is a constant. I also prove similar results concerning the coefficients of general modular forms. I am indebted to Prof. Hardy and Mr Ingham for various suggestions, and in particular to Mr Ingham's paper, “A note on Riemann's ζ-function and Dirichlet's L-functions”.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 35 , Issue 3 , July 1939 , pp. 351 - 356
Copyright
Copyright © Cambridge Philosophical Society 1939

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* Ingham, A. E., J. London. Math. Soc. 5 (1929), 107–12.Google Scholar

† Ramanujan, S., “On certain arithmetical functions”, Collected Papers (Cambridge, 1927), pp. 136–62,Google Scholar or Trans. Cambridge Phil. Soc. 22 (1916), 159–84.Google Scholar

‡ Hardy, G. H., “Note on Ramanujan's function τ(n)”, Proc. Cambridge Phil. Soc. 23 (1927), 675–80.CrossRefGoogle Scholar

* Mordell, L. J., “On Ramanujan's empirical expansions of modular functions”, Proc. Cambridge Phil. Soc. 19 (1920), 117–24.Google Scholar

† This functional equation appears to have been first stated by Wilton, J. R. in “A note on Ramanujan's arithmetical function τ(n)”, Proc. Cambridge Phil. Soc. 25 (1928), 121–9.CrossRefGoogle Scholar Wilton also proves functional equations for more general functions of the form

* Actually as I prove in my second paper.