Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Fremlin, David H.
and
Talagrand, Michel
1979.
On
CS
‐closed sets
.
Mathematika,
Vol. 26,
Issue. 1,
p.
30.
Yost, David
1983.
Banach Space Theory and its Applications.
Vol. 991,
Issue. ,
p.
296.
Borwein, J. M.
1987.
Automatic continuity and openness of convex relations.
Proceedings of the American Mathematical Society,
Vol. 99,
Issue. 1,
p.
49.
1987.
Barrelled Locally Convex Spaces.
Vol. 131,
Issue. ,
p.
484.
Noll, Dominikus
1990.
A topological completeness concept with applications to the open mapping theorem and the separation of convex sets.
Topology and its Applications,
Vol. 35,
Issue. 1,
p.
53.
Simons, S.
1990.
The occasional distributivity of ∘ over+e and the change of variable formula for conjugate functions.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 14,
Issue. 12,
p.
1111.
Penot, J. -P.
1993.
Preservation of persistence and stability under intersections and operations, part 1: Persistence.
Journal of Optimization Theory and Applications,
Vol. 79,
Issue. 3,
p.
525.
Chou, C. C.
and
Penot, J. P.
1995.
Infinite products of relations, set-valued series and uniform openness of multifunctions.
Set-Valued Analysis,
Vol. 3,
Issue. 1,
p.
11.
Dierolf, Susanne
and
Ka̧kol, Jerzy
1995.
On S-Barrelled Spaces.
Results in Mathematics,
Vol. 28,
Issue. 1-2,
p.
40.
Connor, J.
and
Kaufman, W. E.
1995.
OnBH envelopes, convex series, and local completeness.
Archiv der Mathematik,
Vol. 65,
Issue. 1,
p.
39.
Lassonde, Marc
1998.
Minimax Theory and Applications.
Vol. 26,
Issue. ,
p.
135.
Amara, Charki
and
Ciligot-Travain, Marc
1999.
Lower CS-Closed Sets and Functions.
Journal of Mathematical Analysis and Applications,
Vol. 239,
Issue. 2,
p.
371.
Pumplün, D.
2001.
Absolutely convex modules and Saks spaces.
Journal of Pure and Applied Algebra,
Vol. 155,
Issue. 2-3,
p.
257.
Pumplün, Dieter
2002.
The Metric Completion of Convex Sets and Modules.
Results in Mathematics,
Vol. 41,
Issue. 3-4,
p.
346.
Giner, Emmanuel
2009.
Necessary and Sufficient Conditions for the Interchange Between Infimum and the Symbol of Integration.
Set-Valued and Variational Analysis,
Vol. 17,
Issue. 4,
p.
321.
García-Pacheco, Francisco J.
and
Zheng*, Bentuo
2011.
Geometric properties on non-complete spaces.
Quaestiones Mathematicae,
Vol. 34,
Issue. 4,
p.
489.
Penot, Jean-Paul
2013.
Calculus Without Derivatives.
Vol. 266,
Issue. ,
p.
263.
Penot, Jean-Paul
2013.
Calculus Without Derivatives.
Vol. 266,
Issue. ,
p.
1.
Qiu, Jing-Hui
2013.
The domination property for efficiency and Bishop–Phelps theorem in locally convex spaces.
Journal of Mathematical Analysis and Applications,
Vol. 402,
Issue. 1,
p.
133.
Penot, Jean-Paul
2013.
Calculus Without Derivatives.
Vol. 266,
Issue. ,
p.
117.
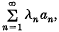 where an∈A and λn ≥ 0 for each n, and
where an∈A and λn ≥ 0 for each n, and 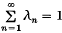 . We say that A is:
. We say that A is:

