Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Sureson, Claude
1986.
ω1-constructible universe and measurable cardinals.
Annals of Pure and Applied Logic,
Vol. 30,
Issue. 3,
p.
293.
Gitik, Moti
1986.
On precipitousness of the nonstationary ideal over a supercompact.
Journal of Symbolic Logic,
Vol. 51,
Issue. 3,
p.
648.
Gitik, Moti
1986.
Changing cofinalities and the nonstationary ideal.
Israel Journal of Mathematics,
Vol. 56,
Issue. 3,
p.
280.
Mitchell, W.
1987.
Applications of the covering lemma for sequences of measures.
Transactions of the American Mathematical Society,
Vol. 299,
Issue. 1,
p.
41.
Drake, F. R.
1987.
European Summer Meeting of the Association for Symbolic Logic, Hull, 1986.
Journal of Symbolic Logic,
Vol. 52,
Issue. 4,
p.
1057.
Mitchell, William
1987.
Prikry forcing at κ+ and beyond.
The Journal of Symbolic Logic,
Vol. 52,
Issue. 1,
p.
44.
Gitik, Moti
1988.
On the Mitchell and Rudin-Kiesler orderings of ultrafilters.
Annals of Pure and Applied Logic,
Vol. 39,
Issue. 2,
p.
175.
Koepke, Peter
1988.
Some applications of short core models.
Annals of Pure and Applied Logic,
Vol. 37,
Issue. 2,
p.
179.
Sureson, Claude
1989.
Chang's model and covering properties.
Annals of Pure and Applied Logic,
Vol. 42,
Issue. 1,
p.
45.
Koepke, Peter
1989.
Logic Colloquium'87, Proceedings of the Colloquium held in Granada.
Vol. 129,
Issue. ,
p.
137.
Gitik, Moti
1989.
On generic elementary embeddings.
Journal of Symbolic Logic,
Vol. 54,
Issue. 3,
p.
700.
Gitik, Moti
1989.
The negation of the singular cardinal hypothesis from o(K)=K++.
Annals of Pure and Applied Logic,
Vol. 43,
Issue. 3,
p.
209.
1990.
Almost Free Modules - Set-theoretic Methods.
Vol. 46,
Issue. ,
p.
456.
Gitik, Moti
1991.
The strenght of the failure of the singular cardinal hypothesis.
Annals of Pure and Applied Logic,
Vol. 51,
Issue. 3,
p.
215.
Mitchell, William J.
1991.
Definable singularity.
Transactions of the American Mathematical Society,
Vol. 327,
Issue. 1,
p.
407.
Mitchell, William J.
1992.
Set Theory of the Continuum.
Vol. 26,
Issue. ,
p.
311.
Mitchell, William J.
1992.
An infinitary Ramsey property.
Annals of Pure and Applied Logic,
Vol. 57,
Issue. 2,
p.
151.
Gitik, Moti
and
Magidor, Menachem
1992.
Set Theory of the Continuum.
Vol. 26,
Issue. ,
p.
243.
Mitchell, W. J.
1992.
On the singular cardinal hypothesis.
Transactions of the American Mathematical Society,
Vol. 329,
Issue. 2,
p.
507.
Apter, Arthur W.
1992.
Some new upper bounds in consistency strength for certain choiceless large cardinal patterns.
Archive for Mathematical Logic,
Vol. 31,
Issue. 3,
p.
201.
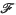 ) presented in this paper is a new inner model of ZFC which can contain measurable cardinals of high order. Like the model L(
) presented in this paper is a new inner model of ZFC which can contain measurable cardinals of high order. Like the model L(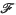 ) of [14], from which it is derived, K(
) of [14], from which it is derived, K(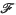 ) is constructed from a sequence
) is constructed from a sequence 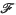 of filters such that K(
of filters such that K(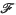 ) satisfies for each (α, β) ε domain (
) satisfies for each (α, β) ε domain (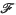 ) that
) that 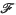 (α,β) is a measure of order β on α and the only measures in K(
(α,β) is a measure of order β on α and the only measures in K(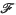 ) are the measures
) are the measures 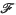 (α,β). Furthermore K(
(α,β). Furthermore K(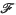 ), like L(
), like L(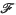 ), has many of the basic properties of L: the GCH and ⃟ hold and there is a definable well ordering which is
), has many of the basic properties of L: the GCH and ⃟ hold and there is a definable well ordering which is 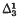 on the reals. The model K(
on the reals. The model K(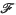 ) is derived from L(
) is derived from L(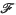 ) by using techniques of Dodd and Jensen [2–5] to build in absoluteness for measurability and related properties.
) by using techniques of Dodd and Jensen [2–5] to build in absoluteness for measurability and related properties.

