Published online by Cambridge University Press: 24 October 2008
Malecot(4) under certain conditions derived the formula 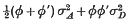 for the covariance of the genotypic values of a quantitative character in two individuals AI and AII, which were related but not by direct descent. This generalized some results of Fisher (l). Kempthorne (2) extended the theory to multiple allelic systems with any degree of epistacy (i.e. interlocular genie interaction) but without linkage. He gave the formula
for the covariance of the genotypic values of a quantitative character in two individuals AI and AII, which were related but not by direct descent. This generalized some results of Fisher (l). Kempthorne (2) extended the theory to multiple allelic systems with any degree of epistacy (i.e. interlocular genie interaction) but without linkage. He gave the formula 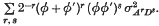 Here
Here 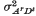 is the item in the population variance which can be attributed to the interaction of additive gene effects at r loci and dominance gene effects at s loci. φ and φ′ are the coefficients of relation between the two individuals. The various assumptions normally included under random mating equilibrium were made, i.e. no selection, mutations, maternal effects or differential viability. Kempthorne (2), (3) gave two rather different proofs of this important result. His second proof was the more straightforward, but it was somewhat condensed.
is the item in the population variance which can be attributed to the interaction of additive gene effects at r loci and dominance gene effects at s loci. φ and φ′ are the coefficients of relation between the two individuals. The various assumptions normally included under random mating equilibrium were made, i.e. no selection, mutations, maternal effects or differential viability. Kempthorne (2), (3) gave two rather different proofs of this important result. His second proof was the more straightforward, but it was somewhat condensed.