Published online by Cambridge University Press: 01 November 2008
Let P(n) = 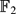 [x1, . . ., xn] = ⊕d≥0Pd(n) be the polynomial algebra viewed as a graded left module over the Steenrod algebra
[x1, . . ., xn] = ⊕d≥0Pd(n) be the polynomial algebra viewed as a graded left module over the Steenrod algebra 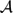 at the prime 2. The grading is by the degree of the homogeneous polynomials Pd(n) of degree d in the n variables x1, . . ., xn. The algebra P(n) realizes the cohomology of the product of n copies of infinite real projective space. We recall that a homogeneous element f of grading d in a graded left
at the prime 2. The grading is by the degree of the homogeneous polynomials Pd(n) of degree d in the n variables x1, . . ., xn. The algebra P(n) realizes the cohomology of the product of n copies of infinite real projective space. We recall that a homogeneous element f of grading d in a graded left 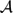 -module M is hit if there is a finite sum f = ΣiSqi(hi), called a hit equation, where the pre-images hi ∈ M have grading strictly less than d and the Sqi, called the Steenrod squares, generate
-module M is hit if there is a finite sum f = ΣiSqi(hi), called a hit equation, where the pre-images hi ∈ M have grading strictly less than d and the Sqi, called the Steenrod squares, generate 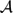 . One of the important parts of the hit problem is to check whether a given polynomial in M is hit or not. In this article we study this problem in the 3-variable case.
. One of the important parts of the hit problem is to check whether a given polynomial in M is hit or not. In this article we study this problem in the 3-variable case.