Differentiation of some classes of set functions
Published online by Cambridge University Press: 24 October 2008
Extract
If A is a subset of a given metric space 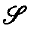 , and F is a function which correlates with each point x of A a family of non-vacuous subsets of
, and F is a function which correlates with each point x of A a family of non-vacuous subsets of 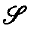 , having the property that there exist members of the family of arbitrarily small diameter, shrinking down upon x, then F is said to be a blanket with domain A. It is well known that if a blanket is endowed with suitable covering properties, then it may be used for the purpose of differentiating one set function with respect to another. It is our intention to consider, in § 3, a type of blanket whose covering families are permitted to overlap in a controlled fashion, and to prove that these may be used for the differentiation of certain set functions with respect to a given one. The paper concludes with the construction, in § 4, of an example which shows that the results achieved are essentially the best possible under the hypotheses.
, having the property that there exist members of the family of arbitrarily small diameter, shrinking down upon x, then F is said to be a blanket with domain A. It is well known that if a blanket is endowed with suitable covering properties, then it may be used for the purpose of differentiating one set function with respect to another. It is our intention to consider, in § 3, a type of blanket whose covering families are permitted to overlap in a controlled fashion, and to prove that these may be used for the differentiation of certain set functions with respect to a given one. The paper concludes with the construction, in § 4, of an example which shows that the results achieved are essentially the best possible under the hypotheses.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 48 , Issue 3 , July 1952 , pp. 374 - 382
- Copyright
- Copyright © Cambridge Philosophical Society 1952
References
REFERENCES
- 3
- Cited by


