Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Williams, W. E.
and
Rosenhead, L.
1961.
Vertex generated waves outside metallic wedges.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 57,
Issue. 2,
p.
393.
Williams, W. E.
1965.
A note on diffraction by a right-angled wedge.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 61,
Issue. 1,
p.
275.
Latz, Norbert
and
Ehrhardt, Joachim
1966.
Untersuchungen über ebene Beugungsprobleme elektromagnetischer Wellen für rechtwinklig-keilförmige Gebiete. Untersuchungen an dielektrischen Stielstrahlern über den Einfluß der Strahlungskopplung auf deren Fußpunktsimpedanz.
p.
5.
Schlak, G. A.
and
Wait, James R.
1967.
ELECTROMAGNETIC WAVE PROPAGATION OVER A NONPARALLEL STRATIFIED CONDUCTING MEDIUM.
Canadian Journal of Physics,
Vol. 45,
Issue. 11,
p.
3697.
Williams, W. E.
1967.
Excitation of multimode surface waves.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 63,
Issue. 4,
p.
1281.
Stuart, W. D.
1970.
Radar Cross Section Handbook.
p.
377.
Bucci, Ovidio M.
and
Franceschetti, Giorgio
1976.
Electromagnetic scattering by a half plane with two face impedances.
Radio Science,
Vol. 11,
Issue. 1,
p.
49.
Molinet, F.
1987.
Geomatrical Theory of Diffraction(GTD) Part I: Foundation of the theory.
IEEE Antennas and Propagation Society Newsletter,
Vol. 29,
Issue. 4,
p.
6.
Hönl, H.
Maue, A. W.
and
Westpfahl, K.
1987.
Kristalloptik · Beugung / Crystal Optics · Diffraction.
Vol. 5 / 25 / 1,
Issue. ,
p.
218.
Poulose, M.M.
and
Mahapatra, P.R.
1988.
ILS glidescope evaluation of imperfect terrain.
IEEE Transactions on Aerospace and Electronic Systems,
Vol. 24,
Issue. 2,
p.
186.
Asghar, S.
and
Hayat, Tasawar
1997.
Scattering of a spherical electromagnetic wave by a metallic strip.
Journal of Modern Optics,
Vol. 44,
Issue. 5,
p.
979.
Asghar, S.
Hayat, Tasawar
and
Ayub, M.
1997.
Diffraction of an electromagnetic wave from an infinitely long slit in an infinite metallic sheet.
International Journal of Infrared and Millimeter Waves,
Vol. 18,
Issue. 9,
p.
1821.
Osipov, Andrey V.
and
Hongo, Kohei
1998.
Green Function of an Impedance Wedge.
Electromagnetics,
Vol. 18,
Issue. 2,
p.
135.
Osipov, A.V.
and
Norris, A.N.
1999.
The Malyuzhinets theory for scattering from wedge boundaries: a review.
Wave Motion,
Vol. 29,
Issue. 4,
p.
313.
Lyalinov, Mikhail A.
and
Zhu, Ning Yan
2013.
Electromagnetic Scattering of a Dipole-Field by an Impedance Wedge, Part I: Far-Field Space Waves.
IEEE Transactions on Antennas and Propagation,
Vol. 61,
Issue. 1,
p.
329.
Tiwana, M.H.
Ahmed, Shakeel
Mann, A.B.
and
Naqvi, Q.A.
2017.
Point source diffraction from a semi-infinite perfect electromagnetic conductor half plane.
Optik,
Vol. 135,
Issue. ,
p.
1.
Umul, Yusuf Ziya
2020.
Wave diffraction by an impedance wedge.
Optik,
Vol. 205,
Issue. ,
p.
164265.
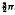 . Previous attempts at solving this problem assumed that the solution could be expressed as a series in inverse powers of the conductivity of the wedge, but this approach can only be applied to wedges of exterior angle less than π as the solution obtained is singular at the edge of the wedge for angles exceeding π. It is shown that in the present case no such expansion is uniformly valid; at large distances from the wedge, however, the present solution agrees with that obtained by assuming an expansion in inverse powers of the conductivity, even though this latter solution is singular at the edge, to order (conductivity of the wedge)−1; the next term in the expansion of the present exact solution is O(conductivity)
. Previous attempts at solving this problem assumed that the solution could be expressed as a series in inverse powers of the conductivity of the wedge, but this approach can only be applied to wedges of exterior angle less than π as the solution obtained is singular at the edge of the wedge for angles exceeding π. It is shown that in the present case no such expansion is uniformly valid; at large distances from the wedge, however, the present solution agrees with that obtained by assuming an expansion in inverse powers of the conductivity, even though this latter solution is singular at the edge, to order (conductivity of the wedge)−1; the next term in the expansion of the present exact solution is O(conductivity)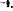 . The case of an incident plane wave may be obtained by letting the source tend to infinity.
. The case of an incident plane wave may be obtained by letting the source tend to infinity.