Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-01-26T07:08:59.525Z Has data issue: false hasContentIssue false
  • English
  • Français

The dimension of self-affine fractals II

Published online by Cambridge University Press:  24 October 2008

K. J. Falconer
K. J. Falconer
Affiliation:
School of Mathematics, University Walk, Bristol BS8 ITW, England
Get access Rights & Permissions [Opens in a new window]

Abstract

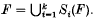A family {S1, ,Sk} of contracting affine transformations on Rn defines a unique non-empty compact set F satisfying . We obtain estimates for the Hausdorff and box-counting dimensions of such sets, and in particular derive an exact expression for the box-counting dimension in certain cases. These estimates are given in terms of the singular value functions of affine transformations associated with the Si. This paper is a sequel to 4, which presented a formula for the dimensions that was valid in almost all cases.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 111 , Issue 1 , January 1992 , pp. 169 - 179
Copyright
Copyright © Cambridge Philosophical Society 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

1Bedford, T.. Crinkly curves, Markov partitions and box dimension in self-similar sets. Ph.D. thesis, University of Warwick (1984).Google Scholar
2Bedford, T.. The box dimension of self-affine graphs and repellers. Nonlinearity 2 (1989), 5371.CrossRefGoogle Scholar
3Bedford, T. and Urbaski, M.. The box and Hausdorff dimension of self-affine sets. Ergodic Theory Dynamical Systems 10 (1990), 627644.CrossRefGoogle Scholar
4Falconer, K. J.. The Hausdorff dimension of self-affine fractals. Math. Proc. Cambridge Philos. Soc. 103 (1988), 339350.CrossRefGoogle Scholar
5Falconer, K. J.. Fractal Geometry Mathematical Foundations and Applications (John Wiley, 1990).Google Scholar
6Hutchinson, J. E.. Fractals and self-similarity. Indiana Univ. Math. J. 30 (1981), 713747.CrossRefGoogle Scholar
7McMullen, C.. The Hausdorff dimension of general Sierpiski carpets. Nagoya Math. J. 96 (1984), 19.CrossRefGoogle Scholar