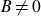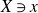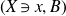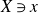Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Han, Jing Jun
and
Luo, Yu Jie
2024.
A Simple Proof of ACC for Minimal Log Discrepancies for Surfaces.
Acta Mathematica Sinica, English Series,
Vol. 40,
Issue. 2,
p.
425.