Published online by Cambridge University Press: 24 October 2008
Given an infinite system of linear equations
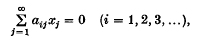
where the aij depend on a parameter λ, the eigenvalue problem is to determine values of λ for which xj (j = 1, 2, …) are not all zero. This problem (Taylor (3) and Vaughan (4)) can arise in the vibration of rectangular plates. Little theoretical work, however, appears to have been done concerning the existence and determination of the eigenvalues. The usual procedure (see (3) and (4)) is to consider a truncated or reduced system of N equations and find the values of λ for which the determinant of the N × N matrix [aij] vanishes. If a particular λ tends to a constant value as N is increased then this value is assumed to be an eigenvalue. The question therefore arises as to what happens if no limit exists. Can we assert that there are no eigenvalues? By constructing an appropriate example we show that the non-existence of a limit does not imply the non-existence of eigenvalues. In order to construct our example we first establish a result concerning the Legendre polynomials.