Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Reade, J. B.
1986.
On the Order of Magnitude of Fourier Coefficients.
SIAM Journal on Mathematical Analysis,
Vol. 17,
Issue. 2,
p.
469.
Glover, Keith
and
Partington, Jonathan R.
1987.
Modelling, Robustness and Sensitivity Reduction in Control Systems.
p.
95.
Oehring, Charles
1989.
Singular numbers of smooth kernels. II.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 105,
Issue. 1,
p.
165.
Glover, K.
Lam, J.
and
Partington, J. R.
1990.
Rational approximation of a class of infinite-dimensional systems I: Singular values of hankel operators.
Mathematics of Control, Signals, and Systems,
Vol. 3,
Issue. 4,
p.
325.
Reade, J. B.
1992.
Eigenvalues of smooth positive definite kernels.
Proceedings of the Edinburgh Mathematical Society,
Vol. 35,
Issue. 1,
p.
41.
Chang, Ching-Hua
and
Ha, Chung-Wei
1999.
Sharp inequalities of singular values of smooth kernels.
Integral Equations and Operator Theory,
Vol. 35,
Issue. 1,
p.
20.
Wathen, Andrew J.
and
Zhu, Shengxin
2015.
On spectral distribution of kernel matrices related to radial basis functions.
Numerical Algorithms,
Vol. 70,
Issue. 4,
p.
709.
Dunker, Fabian
2021.
Adaptive estimation for some nonparametric instrumental variable models with full independence.
Electronic Journal of Statistics,
Vol. 15,
Issue. 2,
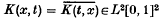 is a symmetric square integrable kernel on the unit square [0, 1]2. Then
is a symmetric square integrable kernel on the unit square [0, 1]2. Then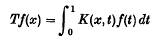
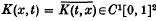 then the eigenvalues
then the eigenvalues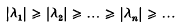
 as n → ∞. We prove a related result. Let W12[0, 1]2 denote the space of all K(x, t) ε L2[0, 1]2 which are absolutely continuous in x for each t and absolutely continuous in t for each x, and the partial derivatives ∂K/∂x(x, t), ∂K/∂t(x, t) are both in L2[0, 1]2. We slow that the eigenvalues of any
as n → ∞. We prove a related result. Let W12[0, 1]2 denote the space of all K(x, t) ε L2[0, 1]2 which are absolutely continuous in x for each t and absolutely continuous in t for each x, and the partial derivatives ∂K/∂x(x, t), ∂K/∂t(x, t) are both in L2[0, 1]2. We slow that the eigenvalues of any 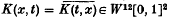 satisfy
satisfy 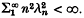 .
.