Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Heath-Brown, D. R.
and
Wilson, P. M. H.
1992.
Calabi-Yau threefolds with ρ>13.
Mathematische Annalen,
Vol. 294,
Issue. 1,
p.
49.
Piene, Ragni
1994.
First European Congress of Mathematics Paris, July 6–10, 1992.
Vol. 120,
Issue. ,
p.
327.
Wilson, P. M. H.
1997.
Symplectic deformations of Calabi-Yau threefolds.
Journal of Differential Geometry,
Vol. 45,
Issue. 3,
Szendröi, B.
2004.
Artin group actions on derived categories of threefolds.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2004,
Issue. 572,
Kapustka, Michał
2009.
Correspondences between modular Calabi–Yau fiber products.
manuscripta mathematica,
Vol. 130,
Issue. 1,
p.
121.
KAPUSTKA, GRZEGORZ
and
KAPUSTKA, MICHAŁ
2009.
FIBER PRODUCTS OF ELLIPTIC SURFACES WITH SECTION AND ASSOCIATED KUMMER FIBRATIONS.
International Journal of Mathematics,
Vol. 20,
Issue. 04,
p.
401.


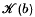 is locally constant in a smooth family
is locally constant in a smooth family 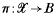 of Calabi–Yau threefolds, unless some of the threefolds
of Calabi–Yau threefolds, unless some of the threefolds 