Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-10T21:24:02.451Z Has data issue: false hasContentIssue false
  • English
  • Français

Explicit methods for the Hasse norm principle and applications to An and Sn extensions

Part of: Algebraic number theory: global fields Linear algebraic groups and related topics Forms and linear algebraic groups Arithmetic problems. Diophantine geometry

Published online by Cambridge University Press:  22 April 2021

ANDRÉ MACEDO  and
RACHEL NEWTON
ANDRÉ MACEDO
Affiliation:
University of Reading, Department of Mathematics and Statistics, Pepper Lane, Whiteknights, Reading RG6 6AX, UK e-mails: c.a.v.macedo@pgr.reading.ac.uk, r.d.newton@reading.ac.uk
RACHEL NEWTON
Affiliation:
University of Reading, Department of Mathematics and Statistics, Pepper Lane, Whiteknights, Reading RG6 6AX, UK e-mails: c.a.v.macedo@pgr.reading.ac.uk, r.d.newton@reading.ac.uk
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let K/k be an extension of number fields. We describe theoretical results and computational methods for calculating the obstruction to the Hasse norm principle for K/k and the defect of weak approximation for the norm one torus 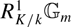\[R_{K/k}^1{\mathbb{G}_m}\] . We apply our techniques to give explicit and computable formulae for the obstruction to the Hasse norm principle and the defect of weak approximation when the normal closure of K/k has symmetric or alternating Galois group.

MSC classification

Primary: 14G05: Rational points
Secondary: 11E72: Galois cohomology of linear algebraic groups 11R37: Class field theory 20G30: Linear algebraic groups over global fields and their integers
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 172 , Issue 3 , May 2022 , pp. 489 - 529
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

References

Altug, S. A., Shankar, A., Varma, I. and Wilson, K. H.. The number of quartic D4-fields ordered by conductor. Preprint. arXiv:1704.01729.Google Scholar
Bartels, H.–J.. Zur Arithmetik von Konjugationsklassen in algebraischen Gruppen. J. Algebra 70 (1981), 179–199.CrossRefGoogle Scholar
Bartels, H.–J.. Zur Arithmetik von Diedergruppenerweiterungen. Math. Ann. 256 (1981), 465–473.CrossRefGoogle Scholar
Bhargava, M.. The density of discriminants of quartic rings and fields. Ann. of Math. 162(2) (2005), 1031–1063.CrossRefGoogle Scholar
Bhargava, M.. The density of discriminants of quintic rings and fields. Ann. of Math. 172(3) (2010) 1559–1591.CrossRefGoogle Scholar
Bhargava, M., Shankar, A. and Tsimerman, J.. On the Davenport–Heilbronn theorems and second order terms. Invent. Math. 193(2) (2013), 439–499.CrossRefGoogle Scholar
Bhargava, M., Shankar, A. and Wang, X.. Geometry-of-numbers methods over global fields I: Prehomogeneous vector spaces. Preprint. arXiv:1704.01729.Google Scholar
Bhargava, M. and Varma, I.. On the mean number of 2-torsion elements in the class groups, narrow class groups, and ideal groups of cubic orders and fields. Duke Math. J. 164(10) (2015), 1911–1933.CrossRefGoogle Scholar
Borovoi, M. and Kunyavskiĭ, B. È.. Formulas for the Unramified Brauer Group of a Principal Homogeneous Space of a Linear Algebraic Group. J. Algebra 225 (2000), 804–821.CrossRefGoogle Scholar
Bosma, W., Cannon, J. and Playoust, C.. The Magma algebra system. I. The user language. J. Symbolic Comput. 24 (1997), 235–265.CrossRefGoogle Scholar
Brown, K. S.. Cohomology of groups. Graduate Texts in Mathematics 87 (Springer–Verlag), 1982.Google Scholar
Browning, T.D.. How often does the Hasse principle hold? Algebraic Geometry: Salt Lake City 2015, Proc. Symposia Pure Math. A.M.S. 97.2 (2018), 89–102.CrossRefGoogle Scholar
Colliot–Thélène, J.-L. and Sansuc, J.–J.. La R-équivalence sur les tores. Ann. Sci. Ecole. Norm. Sup. 10 (1977), 175–229.CrossRefGoogle Scholar
Colliot–Thélène, J.-L. and Sansuc, J.–J.. Principal homogeneous spaces under flasque tori: Applications. J. Algebra 106 (1987), 148–205.CrossRefGoogle Scholar
Datskovsky, B. and Wright, D. J.. Density of discriminants of cubic extensions. J. reine angew. Math. 386 (1988), 116–138.Google Scholar
Drakokhrust, Y. A.. On the complete obstruction to the Hasse principle. Amer. Math. Soc. Transl.(2) 143 (1989), 29–34.Google Scholar
Drakokhrust, Y. A. and Platonov, V. P.. The Hasse norm principle for algebraic number fields. Math. USSR-Izv. 29 (1987), 299–322.CrossRefGoogle Scholar
Ellenberg, J. S., Pierce, L. B. and Wood, M. M.. On $\[\ell \]$ -torsion in class groups of number fields. Algebra and Number Theory 11-8 (2017), 1739–1778.CrossRefGoogle Scholar
Ellenberg, J. S. and Venkatesh, A.. The number of extensions of a number field with fixed degree and bounded discriminant. Ann. of Math. 163(2) (2006), 723–741.CrossRefGoogle Scholar
Fein, B. and Schacher, M.. \[\mathbb{Q}\]-Admissibility Questions for Alternating Groups. J. Algebra 142 (1991), 360–382.CrossRefGoogle Scholar
Frei, C., Loughran, D. and Newton, R.. The Hasse norm principle for abelian extensions. Amer. J. Math 140(6) (2018), 1639–1685.CrossRefGoogle Scholar
Frei, C., Loughran, D. and Newton, R.. with an appendix by Y. Harpaz, O. Wittenberg, Number fields with prescribed norms. Preprint. arXiv:1810.06024.Google Scholar
Frei, C. and Widmer, M.. Average bounds for the $\[\ell \]$ -torsion in class groups of cyclic extensions. Res. Number Theory 4(34) (2018).Google Scholar
GAP Group. GAP – Groups, Algorithms, and Programming, Version 4.8.10 (2018). Available at https://www.gap-system.org.Google Scholar
Gordon, B. and Schacher, M.. Quartic coverings of a cubic. In Number Theory and Algebra, 97–101 (Academic Press, New York, 1977).Google Scholar
Gordon, B. and Schacher, M.. The admissibility of A 5 . J. Number Theory 11 (1979), 489–504.CrossRefGoogle Scholar
Groupprops. The Group Properties Wiki Criterion for element of alternating group to be real. Available at https://groupprops.subwiki.org/wiki/Criterion_for_element_of_alternating_group_to_be_real.Google Scholar
Gurak, S.. On the Hasse norm principle. J. Reine Angew. Math. 299/300 (1978), 16–27.Google Scholar
Gurak, S.. The Hasse norm principle in non-abelian extensions. J. Reine Angew. Math. 0303/0304 (1978), 314–318.Google Scholar
Hasse, H.. Beweis eines Satzes und Wiederlegung einer Vermutung über das allgemeine Normenrestsymbol. Nachr. Ges. Wiss. Göttingen Math.-Phys. Kl. (1931), 64–69.Google Scholar
Higman, D.. Focal series in finite groups. Canad. J. Math. 5 (1953), 477–497.CrossRefGoogle Scholar
Ho, W., Shankar, A. and Varma, I.. Odd degree number fields with odd class number. Duke Math. J. 167 (2018), No. 5, 995–1047.CrossRefGoogle Scholar
Hoffman, P. N. and Humphreys, J. F.. Projective representations of the symmetric groups. Oxford Math. Monogr. (Clarendon Press, Oxford, 1992).Google Scholar
Hoshi, A. and Yamasaki, A.. Rationality problem for algebraic tori. Mem. Amer. Math. Soc. 248 (2017), No. 1176.Google Scholar
Hoshi, A., Kanai, K. and Yamasaki, A.. Norm one tori and Hasse norm principle. Preprint. arXiv:1910.01469.Google Scholar
Hoshi, A., Kanai, K. and Yamasaki, A.. Norm one tori and Hasse norm principle II: degree 12 case. Preprint. arXiv:2003.08253.Google Scholar
Karpilovsky, G.. The Schur Multiplier (Clarendon Press, Oxford, 1987).Google Scholar
Liang, Y.. Non-invariance of weak approximation properties under extension of the ground field. Preprint. arXiv:1805.08851Google Scholar
The LMFDB Collaboration. The L-functions and Modular Forms Database. http://www.lmfdb.org, 2013, [Online; accessed July 2019].Google Scholar
Macedo, A.. GAP code (2019). Available at https://sites.google.com/view/andre-macedo/code.Google Scholar
Macedo, A.. The Hasse norm principle for A n-extensions. J. Number Theory 211 (2020), 500–512.CrossRefGoogle Scholar
Macedo, A.. A note on the density of D 4-fields failing the Hasse norm principle. In preparation.Google Scholar
Malle, G.. On the distribution of Galois groups. J. Number Theory 92(2) (2002), 315–329.CrossRefGoogle Scholar
Pierce, L. B., Turnage-Butterbaugh, C. L. and Wood, M. M.. An effective Chebotarev density theorem for families of number fields, with an application to $\[\ell \]$ -torsion in class groups. Invent. Math. 219 (2020), 701–778.CrossRefGoogle Scholar
Platonov, V. and Rapinchuk, A.. Algebraic groups and number theory. Pure and Applied Mathematics 139 (Academic Press, Inc., Boston, MA, 1994).Google Scholar
Rome, N.. The Hasse norm principle for biquadratic extensions. J. Théor. Nombres Bordeaux 30 No. 3 (2018), 947–964.CrossRefGoogle Scholar
Schacher, M.. Subfields of division rings I. J. Algebra 9 (1968) 451–477.CrossRefGoogle Scholar
Schur, J.. Über die Darstellung der symmetrischen und der alternierenden Gruppe durch gebrochene lineare Substitutionen. J. Reine Angew. Math. 139 (1911), 155–250.Google Scholar
Stern, L.. Equality of norm groups of subextensions of S n (n ≤ 5) extensions of algebraic number fields. J. Number Theory 102(2) (2003), 257–277.CrossRefGoogle Scholar
Tate, J. T.. Global class field theory. pp. 162–203 in: J.W.S. Cassels, A. Fröhlich (eds), Algebraic number theory, Second Edition, London Math. Soc. (2010).Google Scholar
Uchida, K.. Unramified extensions of quadratic number fields I. Tohoku Math. J. 22 (1970), 220–224.Google Scholar
Voskresenskiĭ, V. E.. Birational properties of linear algebraic groups. Izv. Akad. Nauk SSSR Ser. Mat. 34 (1970) 3âĂŞ19. English translation: Math. USSR-Izv. Vol. 4 (1970), 1–17.Google Scholar
Voskresenskiĭ, V. E.. Maximal tori without affect in semisimple algebraic groups, Mat. Zametki 44 (1988) 309–318; English transl. in Math. Notes 44 (1989) 651–655.Google Scholar
Voskresenskiĭ, V. E.. Kunyavskiĭ, B. È.. Maximal tori in semisimple algebraic groups. Manuscript deposited at VINITI 15.03.84, No. 1269-84, 28pp. (in Russian).Google Scholar
Wood, M. M.. Nonabelian Cohen–Lenstra moments (including an appendix with P. M. Wood). Duke Math. J. 168 no. 3 (2019), 377–427.CrossRefGoogle Scholar