Extensions and applications of a tauberian theorem due to valiron
Published online by Cambridge University Press: 24 October 2008
Extract
1. Introduction. In the course of an important memoir on integral functions of finite order†, G. Valiron discusses ‘fonctions orientées’, that is, functions with zeros an such that arg an tends to a limit as n → ∞. He obtains results that include the following two theorems, in which Vρ(x) denotes a function of the form 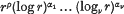 , where α1, …, αν are positive integers, and n(r) has its usual significance in the theory of integral functions:.
, where α1, …, αν are positive integers, and n(r) has its usual significance in the theory of integral functions:.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 47 , Issue 1 , January 1951 , pp. 22 - 37
- Copyright
- Copyright © Cambridge Philosophical Society 1951
References
† Ann. Fac. Sci. Toulouse (3), 5 (1914), 117.Google Scholar
‡ Proc. London Math. Soc. (2), 26 (1926–1947), 185.Google Scholar
§ Quart. J. Math. 19 (1948), 90.Google Scholar
∥ Ann. Math. 49 (1948), 200, 533.Google Scholar
¶ C.R. Acad. Sci., Paris, 228 (1948), 1365.Google Scholar
† Titchmarsh, E. C., Theory of functions (Oxford, 1932), p. 271.Google Scholar
† Valiron, G., Integral functions (Toulouse, 1923), pp. 65–7.Google Scholar
‡ Bull. Soc. Math. France, 35 (1907).Google Scholar
† Proc. London Math. Soc. (2), 38 (1935), 178–9.Google Scholar
- 5
- Cited by


