No CrossRef data available.
Published online by Cambridge University Press: 25 November 2022
On small Seifert fibered spaces
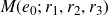 $M(e_0;\,r_1,r_2,r_3)$
with
$M(e_0;\,r_1,r_2,r_3)$
with
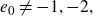 $e_0\neq-1,-2,$
all tight contact structures are Stein fillable. This is not the case for
$e_0\neq-1,-2,$
all tight contact structures are Stein fillable. This is not the case for
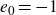 $e_0=-1$
or
$e_0=-1$
or
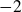 $-2$
. However, for negative twisting structures it is expected that they are all symplectically fillable. Here, we characterise fillable structures among zero-twisting contact structures on small Seifert fibered spaces of the form
$-2$
. However, for negative twisting structures it is expected that they are all symplectically fillable. Here, we characterise fillable structures among zero-twisting contact structures on small Seifert fibered spaces of the form
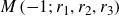 $M\left({-}1;\,r_1,r_2,r_3\right)$
. The result is obtained by analysing monodromy factorizations of associated planar open books.
$M\left({-}1;\,r_1,r_2,r_3\right)$
. The result is obtained by analysing monodromy factorizations of associated planar open books.