No CrossRef data available.
Fixed points on rotating continua
Published online by Cambridge University Press: 24 October 2008
Extract
Suppose I is a bounded plane continuum whose complement is a single domain 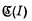 (I) and that
(I) and that 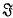 is a (1–1) bicontinuous transformation of the plane onto itself which leaves I invariant. Cartwright and Littlewood(1) have proved the following theorem:
is a (1–1) bicontinuous transformation of the plane onto itself which leaves I invariant. Cartwright and Littlewood(1) have proved the following theorem:
Theorem A. Suppose that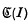 (I) has no prime end fixed under
(I) has no prime end fixed under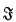 and the frontier of I contains a fixed point P. If
and the frontier of I contains a fixed point P. If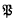 is any prime end of
is any prime end of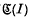 (I) containing P, and C is any curve in
(I) containing P, and C is any curve in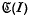 (I) converging to
(I) converging to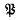 such that PeC¯, the closure of C, then for some‡ integer N the continuum I(FN) consisting of
such that PeC¯, the closure of C, then for some‡ integer N the continuum I(FN) consisting of
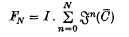
together with the sum B(FN) of its interior complementary domains contains all fixed points in I.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 50 , Issue 1 , January 1954 , pp. 1 - 7
- Copyright
- Copyright © Cambridge Philosophical Society 1954


