A generalized Bernstein approximation theorem
Published online by Cambridge University Press: 24 October 2008
Extract
A celebrated theorem of Weierstrass states that any continuous real-valued function f defined on the closed interval [0, 1] ⊂ ℝ is the limit of a uniformly convergent sequence of polynomials. One of the most elegant and elementary proofs of this classic result is that which uses the Bernstein polynomials of f
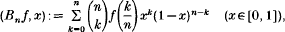
one for each integer n ≥ 1. Bernstein's Theorem states that Bn(f) → f uniformly on [0, 1] and, since each Bn(f) is a polynomial of degree at most n, we have as a consequence Weierstrass' theorem. See for example Lorentz [9]. The operator Bn, defined on the space C([0, 1]; ℝ) with values in the vector subspace of all polynomials of degree at most n has the property that Bn(f) ≥ 0 whenever f ≥ 0. Thus Bernstein's Theorem also establishes the fact that each positive continuous real-valued function on [0, 1] is the limit of a uniformly convergent sequence of positive polynomials. This raises the following natural question: consider a compact Hausdorff space X and the convex cone C+(X):= {f ∈ C(X; ℝ); f ≥ 0}. Now the analogue of Bernstein's Theorem would be a theorem stating when a convex cone contained in C+(X) is dense in it. More generally, one raises the question of describing the closure of a convex cone contained in C(X; ℝ), and, in particular, the closure of A+:= {f ∈ A; f ≥ 0}, where A is a subalgebra of C(X; ℝ).
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 104 , Issue 2 , September 1988 , pp. 317 - 330
- Copyright
- Copyright © Cambridge Philosophical Society 1988
References
REFERENCES
- 13
- Cited by


