No CrossRef data available.
Article contents
Groups generated by two twists along spherical sequences
Published online by Cambridge University Press: 16 May 2022
Abstract
We describe all groups that can be generated by two twists along spherical sequences in an enhanced triangulated category. It will be shown that with one exception such a group is isomorphic to an abelian group generated by not more than two elements, the free group on two generators or the braid group of one of the types
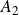 $A_2$
,
$A_2$
,
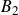 $B_2$
and
$B_2$
and
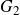 $G_2$
factorised by a central subgroup. The last mentioned subgroup can be nontrivial only if some specific linear relation between length and sphericity holds. The mentioned exception can occur when one has two spherical sequences of length 3 and sphericity 2. In this case the group generated by the corresponding two spherical twists can be isomorphic to the nontrivial central extension of the symmetric group on three elements by the infinite cyclic group. Also we will apply this result to give a presentation of the derived Picard group of selfinjective algebras of the type
$G_2$
factorised by a central subgroup. The last mentioned subgroup can be nontrivial only if some specific linear relation between length and sphericity holds. The mentioned exception can occur when one has two spherical sequences of length 3 and sphericity 2. In this case the group generated by the corresponding two spherical twists can be isomorphic to the nontrivial central extension of the symmetric group on three elements by the infinite cyclic group. Also we will apply this result to give a presentation of the derived Picard group of selfinjective algebras of the type
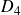 $D_4$
with torsion 3 by generators and relations.
$D_4$
with torsion 3 by generators and relations.
MSC classification
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 174 , Issue 1 , January 2023 , pp. 137 - 161
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Cambridge Philosophical Society


