Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-28T00:19:24.773Z Has data issue: false hasContentIssue false
  • English
  • Français

The growth of univalent functions with an initial gap II

Published online by Cambridge University Press:  10 April 2007

DOV AHARONOV  and
WALTER K. HAYMAN
DOV AHARONOV
Affiliation:
Department of Mathematics, Technion–Israel Institute of Technology, Haifa, 32000Israel. e-mail: dova@tx.technion.ac.il
WALTER K. HAYMAN
Affiliation:
Imperial College, London SW7 2AZ. e-mail: w.hayman@imperial.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the class Sp of functions 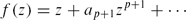univalent in the unit disk Δ.

In [1] it was shown that if f∈Sp and p is large, (0.1)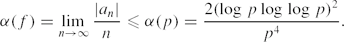 Here we show that there exists f in Sp for p=1,2,. . . such that 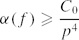where C0 is a positive absolute constant.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 142 , Issue 2 , March 2007 , pp. 305 - 318
Copyright
Copyright © Cambridge Philosophical Society 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Aharonov, D., Hayman, W. K. and Pommerenke, Ch.. The growth of univalent functions with an initial gap I. Math. Proc. Camb. Phil. Soc., 140 (2006), 305–312.CrossRefGoogle Scholar
[2] Duren, P. L.. Univalent Functions (Springer, 1983).Google Scholar
[3] Eremenko, A. and Hayman, W. K.. Univalent functions of fast growth with gap power series. Math. Proc. Camb. Phil. Soc. 127 (1999), 525–532.CrossRefGoogle Scholar
[4] Hayman, W. K.. Multivalent Functions (2nd edition) (Cambridge University Press, 1994).CrossRefGoogle Scholar
[5] Nehari, Z..Conformal Mapping (Mc Graw-Hill Book Company, 1952).Google Scholar