No CrossRef data available.
A ‘Hardy–Littlewood’ approach to the norm form equation
Published online by Cambridge University Press: 24 October 2008
Extract
Suppose that K is a number field and n = [K: ℚ]. Write S∞(K) for the set of archimedean places of K, i.e. the set of all embeddings σ: K → ℂ. Suppose that 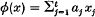 is a linear form in t variables x1, …, xt, where the aj ∈ K. This gives rise to a norm form N(x), where
is a linear form in t variables x1, …, xt, where the aj ∈ K. This gives rise to a norm form N(x), where

- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 104 , Issue 3 , November 1988 , pp. 421 - 427
- Copyright
- Copyright © Cambridge Philosophical Society 1988
References
REFERENCES
[1]Baker, A. and Masser, D. W.. Transcendence Theory: Advances and Applications (Academic Press, 1977).Google Scholar
[2]Everest, G. R.. Diophantine approximation and the distribution of normal integral generators. J. London Math. Soc. (2) 28 (1983), 227–237.CrossRefGoogle Scholar
[3]Everest, G. R.. Angular distribution of units in abelian group rings – an application to Galois-module theory. J. reine angew. Math. 375 (1987), 24–41.Google Scholar
[4]Everest, G. R.. Units in abelian group rings and meromorphic functions. Illinois J. Math. (to appear).Google Scholar
[5]Evertse, J.-H.. On sums of S-units and linear recurrences. Compositio Math. 53 (1984), 225–244.Google Scholar
[6]Evertse, J.-H. and Györy, K.. On unit equations and decomposable form equations. J. reine angew. Math. 358 (1985), 6–19.Google Scholar
[8]Schmidt, W. M.. Diophantine Approximation. Lecture notes in Math, vol. 785 (Springer-Verlag, 1980).Google Scholar


