Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-10T22:02:04.376Z Has data issue: false hasContentIssue false
  • English
  • Français

Hausdorff dimension of the set of elliptic functions with critical values approaching infinity

Published online by Cambridge University Press:  01 October 2012

PIOTR GAŁĄZKA
PIOTR GAŁĄZKA*
Affiliation:
Faculty of Mathematics and Information Science, Warsaw University of Technology, Warsaw 00-661, Poland. e-mail: P.Galazka@mini.pw.edu.pl
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 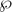Λ denote the Weierstrass function with a period lattice Λ. We consider escaping parameters in the family β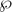Λ, i.e. the parameters β for which the orbits of all critical values of β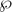Λ approach infinity under iteration. Unlike the exponential family, the functions considered here are ergodic and admit a non-atomic, σ-finite, ergodic, conservative and invariant measure μ absolutely continuous with respect to the Lebesgue measure. Under additional assumptions on 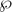Λ, we estimate the Hausdorff dimension of the set of escaping parameters in the family β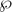Λ from below, and compare it with the Hausdorff dimension of the escaping set in the dynamical space, proving a similarity between the parameter plane and the dynamical space.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 154 , Issue 1 , January 2013 , pp. 97 - 118
Copyright
Copyright © Cambridge Philosophical Society 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bergweiler, W., Karpińska, B. and Stallard, G. M.The growth rate of an entire function and the Hausdorff dimension of its Julia set. J. Lond. Math. Soc. 80 (2009), 680–698.CrossRefGoogle Scholar
[2]Bergweiler, W. and Kotus, J. On the Hausdorff dimension of the escaping set of certain meromorphic functions, to appear in Trans. Amer. Math. Soc., arxiv: 0901.3014.Google Scholar
[3]Bergweiler, W., Rippon, P. J. and Stallard, G. M.Dynamics of meromorphic functions with direct or logarithmic singularities. Proc. Lond. Math. Soc. 97 (2008), 368–400.CrossRefGoogle Scholar
[4]Domínguez, P.Dynamics of transcendental meromorphic functions. Ann. Acad. Sci. Fenn. Math. 23 (1998), 225–250.Google Scholar
[5]Hawkins, J. and Koss, L.Connectivity of Julia sets of Weierstrass elliptic functions. Topology Appl. 152 (2002), 107–137.CrossRefGoogle Scholar
[6]Hawkins, J. and Koss, L.Ergodic properties and Julia sets of Weierstrass elliptic functions. Monatsh. Math. 137 (2002), 273–300.CrossRefGoogle Scholar
[7]Hawkins, J. and Koss, L.Parametrized dynamics of the Weierstrass elliptic functions. Conform. Geom. Dyn. 8 (2004), 1–35.CrossRefGoogle Scholar
[8]Hawkins, J., Koss, L. and Kotus, J.Elliptic functions with critical orbits approaching infinity. J. Difference Equ. Appl. 16 (2010), 613–630.CrossRefGoogle Scholar
[9]Hemke, J. M.Recurrence of entire transcendental functions with simple post-singular sets. Fund. Math. 187 (2005), 255–289.CrossRefGoogle Scholar
[10]Kotus, J.On the Hausdorff dimension of Julia sets of meromorphic functions II. Bull. Soc. Math. France 123 (1995), 33–46.CrossRefGoogle Scholar
[11]Kotus, J. and Urbański, M.Existence of invariant measures for transcendental subexpanding functions. Math. Zeit. 243 (2003), 25–36.CrossRefGoogle Scholar
[12]Kotus, J. and Urbański, M.Hausdorff dimension and Hausdorff measures of Julia sets of elliptic functions. Bull. Lond. Math. Soc. 35 (2003), 269–275.CrossRefGoogle Scholar
[13]Kotus, J. and Urbański, M.Geometry and ergodic theory of non-recurrent elliptic functions. J. Anal. Math. 93 (2004), 35–102.CrossRefGoogle Scholar
[14]Kotus, J. and Urbański, M. The class of pseudo non-recurrent elliptic functions; geometry and dynamics, preprint available at www.math.unt.edu/~urbanskiGoogle Scholar
[15]Yu, M.Lyubich. Measurable dynamics of the exponential. Sib. Math. J. 28 (1988), 780–793.Google Scholar
[16]McMullen, C.Area and Hausdorff dimension of Julia sets of entire functions. Trans. Amer. Math. Soc. 300 (1987), 329–342.CrossRefGoogle Scholar
[17]Rippon, P. J. and Stallard, G. M.Iteration of a class of hyperbolic meromorphic functions. Proc. Amer. Math. Soc. 127 (1999), 3251–3258.CrossRefGoogle Scholar
[18]Rippon, P. J. and Stallard, G. M.Escaping points of meromorphic functions with a finite number of poles. J. Anal. Math. 96 (2005), 225–245.CrossRefGoogle Scholar
[19]Rippon, P. J. and Stallard, G. M.Escaping points of entire functions of small growth. Math. Zeit. 261 (2009), 557–570.CrossRefGoogle Scholar
[20]Urbański, M. and Zdunik, A.Geometry and ergodic theory of non-hyperbolic exponential maps. Trans. Amer. Math. Soc. 359 (2007), 3973–3997.CrossRefGoogle Scholar