Published online by Cambridge University Press: 24 October 2008
Let p(x) be periodic with mean value c and let α > 0. Then the investigation of the asymptotic solution of the second-order equation
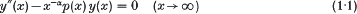
can be split into four cases: (i) α > 2, (ii) α > 1 and c = 0, (iii) 0 < α ≤ 1 and c = 0, (iv) 0 < α ≤ 2 and c ≠ 0. The first two cases are straightforward because then there are solutions y1 and y2 of (1·1) such that y1(x) ~ x and y2(x) → 1 as x → ∞ [5, theorems 2·7·2 and 2·7·5; 7, p. 375; 8]. Thus the coefficient of y in (1·1) represents a perturbation which has no effect on the dominant asymptotic behaviour of solutions. Case (iii) is less simple because here the nature of p(x) does influence the asymptotic form of solutions and, indeed, when α < 1 the solutions of (1·1) are oscillatory. This case has been fully covered by a number of authors: Atkinson, Eastham and McLeod[2, §3], Cassell[3, 4], Eastham[5, §4·13], Mahoney[10], Willett[13] and Wong[14, 15]. In addition, corresponding results for a higher-order self-adjoint analogue of (1·1) have been obtained recently by Al-Hammadi and Eastham [1, 6] as an application of general asymptotic methods for differential systems.