Article contents
The Hilbert transform of Schwartz distributions. II
Published online by Cambridge University Press: 24 October 2008
Abstract
Let D(R) be the Schwartz space of C∞ functions with compact support on R and let H(D) be the space of all C∞ functions defined on R for which every element is the Hilbert transform of an element in D(R), i.e.
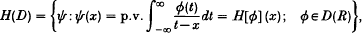
where the integral is defined in the Cauchy principal-value sense. Introducing an appropriate topology in H(D), Pandey [3] defined the Hilbert transform Hf of f ∈ (D(R))′ as an element of (H(D))′ by the relation
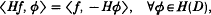
and then with an appropriate interpretation he proved that
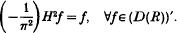 .
.
In this paper we give an intrinsic description of the space H(D) and its topology, thereby providing a solution to an open problem posed by Pandey ([4], p. 90).
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 102 , Issue 3 , November 1987 , pp. 553 - 559
- Copyright
- Copyright © Cambridge Philosophical Society 1987
References
REFERENCES
- 4
- Cited by


