Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Dicks, Warren
1988.
Ring Theory.
Vol. 1328,
Issue. ,
p.
75.


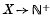 . We show that the idealizer of
. We show that the idealizer of 