Article contents
Homothetic ellipsoids1
Published online by Cambridge University Press: 24 October 2008
Abstract
We let K1 and K2 be two convex bodies in Ed (d ≥ 3) and consider translates 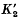 of K2 for which ∂K1 ∩ ∂
of K2 for which ∂K1 ∩ ∂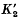 ≠ ø and K1 ≠
≠ ø and K1 ≠ 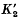 . We show that if, for all such translates,∂K1 ∩
. We show that if, for all such translates,∂K1 ∩ 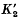 is contained in a hyperplane then K1 and K2 are homothetic ellipsoids.
is contained in a hyperplane then K1 and K2 are homothetic ellipsoids.
If K1 and K2 are two planar non-coincident convex sets whose interiors intersect we define α(K1, K2) to be the number of connected components of ∂K1 ∩ ∂K2. The starting point for our investigations is the result of Fujiwara(S) and Bol(2) to the effect that K is a circular disc if and only if α(K, K′) = 2 for all congruent copies K′ of K. An easy extension of this result is the observation that K1 and K2 are congruent circular discs if and only if 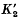 for all congruent copies
for all congruent copies 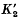 of K2. When working with such results it is natural to look for analogues in the situation where only translates are allowed rather than all possible congruences. The appropriate analogue was obtained in (7) and we state it here for completeness.
of K2. When working with such results it is natural to look for analogues in the situation where only translates are allowed rather than all possible congruences. The appropriate analogue was obtained in (7) and we state it here for completeness.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 93 , Issue 1 , January 1983 , pp. 25 - 34
- Copyright
- Copyright © Cambridge Philosophical Society 1983
References
REFERENCES
- 10
- Cited by


