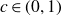1. Introduction
Let
![]() $[N] = \{1,\ldots, N\}$
and
$[N] = \{1,\ldots, N\}$
and
![]() $r_k(N)$
denote the size of the largest
$r_k(N)$
denote the size of the largest
![]() $S\subseteq\{1,\ldots, N\}$
such that S has no k-term arithmetic progressions. The first nontrivial upper bound on
$S\subseteq\{1,\ldots, N\}$
such that S has no k-term arithmetic progressions. The first nontrivial upper bound on
![]() $r_3(N)$
came from work of Roth [
Reference Roth28
] which proved
$r_3(N)$
came from work of Roth [
Reference Roth28
] which proved
A long series of works improved the bounds in the case
![]() $k=3$
. This includes works of Heath–Brown [
Reference Heath-Brown16
], Szemerédi [
Reference Szemerédi35
], Bourgain [
Reference Bourgain5, Reference Bourgain6
], Sanders [
Reference Sanders30, Reference Sanders31
], Bloom [
Reference Bloom2
], and Bloom and Sisask [
Reference Bloom and Sisask3
]. Recently, in breakthrough work, Kelley and Meka [
Reference Kelley and Meka18
] proved that
$k=3$
. This includes works of Heath–Brown [
Reference Heath-Brown16
], Szemerédi [
Reference Szemerédi35
], Bourgain [
Reference Bourgain5, Reference Bourgain6
], Sanders [
Reference Sanders30, Reference Sanders31
], Bloom [
Reference Bloom2
], and Bloom and Sisask [
Reference Bloom and Sisask3
]. Recently, in breakthrough work, Kelley and Meka [
Reference Kelley and Meka18
] proved that
modulo the constant
![]() $1/12$
this matches the lower bound construction of Behrend [
Reference Behrend1
]. The constant
$1/12$
this matches the lower bound construction of Behrend [
Reference Behrend1
]. The constant
![]() $1/12$
was refined to
$1/12$
was refined to
![]() $1/9$
in work of Bloom and Sisask [
Reference Bloom and Sisask4
].
$1/9$
in work of Bloom and Sisask [
Reference Bloom and Sisask4
].
For higher k, establishing that
![]() $r_k(N) = o(N)$
was a long standing conjecture of Erdös and Turán. In seminal works, Szemerédi [
Reference Szemerédi33
] first established the estimate
$r_k(N) = o(N)$
was a long standing conjecture of Erdös and Turán. In seminal works, Szemerédi [
Reference Szemerédi33
] first established the estimate
![]() $r_4(N) = o(N)$
and then in later work Szemerédi [
Reference Szemerédi34
] established his eponymous theorem that
$r_4(N) = o(N)$
and then in later work Szemerédi [
Reference Szemerédi34
] established his eponymous theorem that
Due to the uses of van der Waerden theorem and the regularity lemma (which was introduced in this work), Szemerédi’s estimate was exceedingly weak. In seminal work Gowers [ Reference Gowers7, Reference Gowers8 ] introduced higher order Fourier analysis and proved the first “reasonable” bounds for Szemerédi’s theorem:
The only previous improvement to this result for
![]() $k\ge 4$
was work on the case
$k\ge 4$
was work on the case
![]() $k=4$
of Green and Tao [
Reference Green and Tao13, Reference Green and Tao14
] which ultimately established that
$k=4$
of Green and Tao [
Reference Green and Tao13, Reference Green and Tao14
] which ultimately established that
Our main result is a “quasi-logarithmic” bound in the case
![]() $k = 5$
.
$k = 5$
.
Theorem 1·1. There is
![]() $c\in(0,1)$
such that
$c\in(0,1)$
such that
Remark. Throughout this paper, we will abusively write
![]() $\log$
for
$\log$
for
![]() $\max(\!\log\!(\cdot), e^e)$
. This is to avoid trivial issues regarding inputs which are small.
$\max(\!\log\!(\cdot), e^e)$
. This is to avoid trivial issues regarding inputs which are small.
Our work relies crucially on a recent improved inverse theorem for the Gowers
![]() $U^4$
-norm due to the first author [
Reference Leng23
, theorem 7]. We first formally define the Gowers
$U^4$
-norm due to the first author [
Reference Leng23
, theorem 7]. We first formally define the Gowers
![]() $U^k$
-norm.
$U^k$
-norm.
Definition 1·2. Given
![]() $f\colon\mathbb{Z}/N\mathbb{Z}\to\mathbb{C}$
and
$f\colon\mathbb{Z}/N\mathbb{Z}\to\mathbb{C}$
and
![]() $k\ge 1$
, we define
$k\ge 1$
, we define
where
![]() $\Delta_hf(x)=f(x)\overline{f(x+h)}$
is the multiplicative discrete derivative (extended to vectors h in the natural way). This is known to be well-defined and a norm (seminorm if
$\Delta_hf(x)=f(x)\overline{f(x+h)}$
is the multiplicative discrete derivative (extended to vectors h in the natural way). This is known to be well-defined and a norm (seminorm if
![]() $k=1$
).
$k=1$
).
Theorem 1·3. There exists an absolute constant
![]() $C\ge 1$
such that the following holds. Let N be prime, let
$C\ge 1$
such that the following holds. Let N be prime, let
![]() $\delta \gt 0$
, and suppose that
$\delta \gt 0$
, and suppose that
![]() $f\colon\mathbb{Z}/N\mathbb{Z}\to\mathbb{C}$
is a 1-bounded function with
$f\colon\mathbb{Z}/N\mathbb{Z}\to\mathbb{C}$
is a 1-bounded function with
There exists a degree 3 nilsequence
![]() $F(g(n)\Gamma)$
such that it has dimension bounded by
$F(g(n)\Gamma)$
such that it has dimension bounded by
![]() $(\!\log\!(1/\delta))^C$
, complexity bounded by C, such that F is 1-Lipschitz, and such that
$(\!\log\!(1/\delta))^C$
, complexity bounded by C, such that F is 1-Lipschitz, and such that
A key manoeuvre in this paper is our deduction of a variant of the
![]() $U^4$
-inverse theorem which lends itself to the analysis of multiple nilsequences simultaneously and may be of independent interest. Although it is known that having a large
$U^4$
-inverse theorem which lends itself to the analysis of multiple nilsequences simultaneously and may be of independent interest. Although it is known that having a large
![]() $U^4$
-norm does not necessarily imply direct correlation with a cubic phase function due to the existence of bracket polynomials, one can hope to achieve correlation on a dense, structured host set (for us, a Bohr set).
$U^4$
-norm does not necessarily imply direct correlation with a cubic phase function due to the existence of bracket polynomials, one can hope to achieve correlation on a dense, structured host set (for us, a Bohr set).
Proposition 1·4. There exists an absolute constant
![]() $C\ge 1$
such that the following holds. Let N be prime, let
$C\ge 1$
such that the following holds. Let N be prime, let
![]() $\delta \gt 0$
, and suppose that
$\delta \gt 0$
, and suppose that
![]() $f\colon\mathbb{Z}/N\mathbb{Z}\to\mathbb{C}$
is a 1-bounded function with
$f\colon\mathbb{Z}/N\mathbb{Z}\to\mathbb{C}$
is a 1-bounded function with
There exist
![]() $S\subseteq (1/N)\mathbb{Z}$
with
$S\subseteq (1/N)\mathbb{Z}$
with
![]() $|S|\ll (\!\log\!(1/\delta))^C$
, and
$|S|\ll (\!\log\!(1/\delta))^C$
, and
![]() $y\in\mathbb{Z}/N\mathbb{Z}$
such that the following holds: there is a locally cubic phase function
$y\in\mathbb{Z}/N\mathbb{Z}$
such that the following holds: there is a locally cubic phase function
![]() $\phi\colon y+B(S,1/100)\to\mathbb{R}/\mathbb{Z}$
such that
$\phi\colon y+B(S,1/100)\to\mathbb{R}/\mathbb{Z}$
such that
We refer the reader to Definitions 2·1 and 2·2 for precise definitions of Bohr set and locally cubic phase function. We remark that an analogous result to Proposition 2·3 for higher
![]() $U^k$
-norms is false; this can be seen by examining the function
$U^k$
-norms is false; this can be seen by examining the function
![]() $e(\{an\{bn\}\}\{cn\} dn)$
. We discuss this issue in more detail in Section 1·1.
$e(\{an\{bn\}\}\{cn\} dn)$
. We discuss this issue in more detail in Section 1·1.
1·1. Proof outline
The starting point of our work involves combining the density increment strategy of Heath-Brown [
Reference Heath-Brown16
] and Szemerédi [
Reference Szemerédi35
], which was reformulated in a robust manner by Green and Tao [
Reference Green and Tao13
] when proving that
![]() $r_4(N)\ll N\exp\!(\!-\!\Omega(\sqrt{\log\log N}))$
, with the improved
$r_4(N)\ll N\exp\!(\!-\!\Omega(\sqrt{\log\log N}))$
, with the improved
![]() $U^4$
-inverse theorem Theorem 1·3 of the first author. The crucial difference between the density increment strategy of Roth [
Reference Roth28
] versus Heath-Brown [
Reference Heath-Brown16
] and Szemerédi [
Reference Szemerédi35
] is that one finds correlations with “many functions” to deduce a density increment.
$U^4$
-inverse theorem Theorem 1·3 of the first author. The crucial difference between the density increment strategy of Roth [
Reference Roth28
] versus Heath-Brown [
Reference Heath-Brown16
] and Szemerédi [
Reference Szemerédi35
] is that one finds correlations with “many functions” to deduce a density increment.
If we apply Theorem 1·3 directly with the density increment strategy as codified by Green and Tao [
Reference Green and Tao13
], we would at the very least need that, given a polynomial sequence g(n) with
![]() $g(0) = \operatorname{id}_{G}$
on a nilmanifold
$g(0) = \operatorname{id}_{G}$
on a nilmanifold
![]() $G/\Gamma$
of degree 3 with complexity M and dimension d, we have
$G/\Gamma$
of degree 3 with complexity M and dimension d, we have
When g(n) is a polynomial sequence of degree 3 on the torus such results can be derived from work of Schmidt [ Reference Schmidt32 ] on small fractional parts of polynomials. While directly deriving such a result for nonabelian nilmanifolds does not appear implausible, at present the distribution theory of nilmanifolds only has such “polynomial in d” dependencies when dealing with test functions having vertical frequency, due to work of the first author [ Reference Leng22 ].
The crucial step in our work therefore is solving such a Schmidt-type problem for nilmanifolds via representing 3-step nilmanifolds as sums of exponentials of locally cubic functions on Bohr sets (see Proposition 2·3). The analogue of such a result for 2-step nilmanifolds (without bounds) appears in work of Green and Tao [
Reference Green and Tao10
, proposition 2·3]. That such a result is true is a miracle of small numbers which is most easily seen via bracket polynomials. (In work of Green and Tao [
Reference Green and Tao13
] regarding
![]() $r_4(N)$
, one operates with a version of the
$r_4(N)$
, one operates with a version of the
![]() $U^3$
-inverse theorem proven directly for locally quadratic functions on Bohr sets.)
$U^3$
-inverse theorem proven directly for locally quadratic functions on Bohr sets.)
At an informal level, the
![]() $U^4$
-inverse theorem may be rephrased as follows: if
$U^4$
-inverse theorem may be rephrased as follows: if
![]() $\lVert f\rVert_{U^4}$
is large for 1-bounded f, then f correlates with a bracket exponential phase e(H(n)) where H(n) is (essentially) a sum of terms of the form
$\lVert f\rVert_{U^4}$
is large for 1-bounded f, then f correlates with a bracket exponential phase e(H(n)) where H(n) is (essentially) a sum of terms of the form
plus terms which are obviously of “lower degree”. By the work of Green and Tao, various lower order terms may be viewed as quadratic functions on Bohr sets. Now note that
Therefore
Furthermore note that
![]() $e(\{x\}\{y\})$
is, after appropriate smoothing, a Lipschitz function on
$e(\{x\}\{y\})$
is, after appropriate smoothing, a Lipschitz function on
![]() $(\mathbb{R}/\mathbb{Z})^2$
and therefore is well-approximated by a weighted sum of exponentials of the form
$(\mathbb{R}/\mathbb{Z})^2$
and therefore is well-approximated by a weighted sum of exponentials of the form
![]() $e(kx + \ell y)$
for
$e(kx + \ell y)$
for
![]() $k,\ell\in \mathbb{Z}$
. Given this (and noting the analogous fact for
$k,\ell\in \mathbb{Z}$
. Given this (and noting the analogous fact for
![]() $e(\{x\}\{y\}\{z\})$
) we may rewrite our basis of degree 3 functions as
$e(\{x\}\{y\}\{z\})$
) we may rewrite our basis of degree 3 functions as
the most crucial of these manipulations is
The miracle is that we do not have any nested
![]() $\{\cdot\}$
and all of the brackets surround linear functions. Therefore, upon restricting the fractional parts to lie in certain narrow ranges away from the discontinuities in the fraction part (i.e., Bohr set-type conditions) the functions
$\{\cdot\}$
and all of the brackets surround linear functions. Therefore, upon restricting the fractional parts to lie in certain narrow ranges away from the discontinuities in the fraction part (i.e., Bohr set-type conditions) the functions
![]() $an^2\{bn\}, an\{bn\}\{cn\}$
are seen to be “locally cubic”. That is, discrete fourth-order derivatives vanish given that all points in the corresponding 4-dimensional hypercube lie in an appropriate Bohr set. The existence of such a miracle can be seen by examining carefully all “fractional part” expressions required in work of Green–Tao–Ziegler [
Reference Green, Tao and Ziegler12
, appendix E] on the
$an^2\{bn\}, an\{bn\}\{cn\}$
are seen to be “locally cubic”. That is, discrete fourth-order derivatives vanish given that all points in the corresponding 4-dimensional hypercube lie in an appropriate Bohr set. The existence of such a miracle can be seen by examining carefully all “fractional part” expressions required in work of Green–Tao–Ziegler [
Reference Green, Tao and Ziegler12
, appendix E] on the
![]() $U^4$
-inverse theorem. For the
$U^4$
-inverse theorem. For the
![]() $U^5$
-inverse theorem and higher, we have the function
$U^5$
-inverse theorem and higher, we have the function
![]() $e(\{an\{bn\}\}\{cn\} dn)$
and fractional part identities do not allow one to “remove iterated floor functions”.
$e(\{an\{bn\}\}\{cn\} dn)$
and fractional part identities do not allow one to “remove iterated floor functions”.
To actually prove the desired representation of a step 3 nilsequence, we partition the nilmanifold via a partition of unity. Operating within a partition of unity, we may manipulate the nilmanifold (as in [ Reference Green and Tao10 , proposition 2·3]) via explicitly operating in Mal’cev coordinates of the first kind. This allows us to manipulate the floor and fractional expressions as suggested by the bracket polynomial formalism in the previous paragraphs. Identifying various fundamental domains with the torus and applying Fourier expansion appropriately eventually gives the desired decomposition.
We remark for technical reasons it turns out to be useful to manipulate our nilsequence to be N-periodic and living on a nilmanifold for which the Lie bracket structure constants are integers which are sufficiently divisible. The first task is accomplished via appropriately quantifying a construction of Manners [
Reference Manners24
] (see Proposition C·2) and the second is accomplished via a “clearing denominators” trick on the Mal’cev basis (see Lemma C·1). One can see that such a manipulation might be useful by noting that if the structure constants of
![]() $G/\Gamma$
are sufficiently divisible then
$G/\Gamma$
are sufficiently divisible then
![]() $\psi_{\exp}(\Gamma) = \mathbb{Z}^d$
where
$\psi_{\exp}(\Gamma) = \mathbb{Z}^d$
where
![]() $\psi_{\exp}$
is the map to Mal’cev coordinates of the first kind (see Lemma 2·5). In general
$\psi_{\exp}$
is the map to Mal’cev coordinates of the first kind (see Lemma 2·5). In general
![]() $\psi_{\exp}(\Gamma)$
is not even a lattice in
$\psi_{\exp}(\Gamma)$
is not even a lattice in
![]() $\mathbb{Q}^d$
.
$\mathbb{Q}^d$
.
Finally, given a correlation with a locally cubic function on a Bohr set, we are now in position to run the density increment strategy of Heath-Brown [
Reference Heath-Brown16
] and Szemerédi [
Reference Szemerédi35
] as codified by Green and Tao [
Reference Green and Tao13
]. Our proof is very close to that of Green and Tao [
Reference Green and Tao13
], although there are slight simplifications afforded in our situation since the dimension of our Bohr sets are “quasi-logarithmic”. In particular, it is possible to operate by considering single atoms in the Bohr partition and avoid the use of regular Bohr sets. Our situation at this point is closely analogous to having access to the
![]() $U^3$
-inverse theorem of Sanders [
Reference Sanders29
] and aiming to prove bounds of the form
$U^3$
-inverse theorem of Sanders [
Reference Sanders29
] and aiming to prove bounds of the form
![]() $r_4(N)\ll N \exp\!(\!-\!(\!\log\log N)^c)$
.
$r_4(N)\ll N \exp\!(\!-\!(\!\log\log N)^c)$
.
Notation. We use standard asymptotic notation. Given functions
![]() $f=f(n)$
and
$f=f(n)$
and
![]() $g=g(n)$
, we write
$g=g(n)$
, we write
![]() $f=O(g)$
,
$f=O(g)$
,
![]() $f \ll g$
,
$f \ll g$
,
![]() $g=\Omega(f)$
, or
$g=\Omega(f)$
, or
![]() $g\gg f$
to mean that there is a constant C such that
$g\gg f$
to mean that there is a constant C such that
![]() $|f(n)|\le Cg(n)$
for sufficiently large n. We write
$|f(n)|\le Cg(n)$
for sufficiently large n. We write
![]() $f\asymp g$
or
$f\asymp g$
or
![]() $f=\Theta(g)$
to mean that
$f=\Theta(g)$
to mean that
![]() $f\ll g$
and
$f\ll g$
and
![]() $g\ll f$
, and write
$g\ll f$
, and write
![]() $f=o(g)$
or
$f=o(g)$
or
![]() $g=\omega(f)$
to mean
$g=\omega(f)$
to mean
![]() $f(n)/g(n)\to0$
as
$f(n)/g(n)\to0$
as
![]() $n\to\infty$
. Subscripts on asymptotic notation indicate dependence of the bounds on those parameters. We will use the notation
$n\to\infty$
. Subscripts on asymptotic notation indicate dependence of the bounds on those parameters. We will use the notation
![]() $[x] = \{1,2\ldots,\lfloor x\rfloor\}$
.
$[x] = \{1,2\ldots,\lfloor x\rfloor\}$
.
We use the notations of Appendix A with regards to nilmanifolds. Write
![]() $\Delta_hf(x)=f(x)\overline{f(x+h)}$
for the multiplicative discete derivative and
$\Delta_hf(x)=f(x)\overline{f(x+h)}$
for the multiplicative discete derivative and
![]() $\partial_hf(x)=f(x)-f(x+h)$
for the additive discrete derivative (for functions over appropriate domains and codomains). The Gowers
$\partial_hf(x)=f(x)-f(x+h)$
for the additive discrete derivative (for functions over appropriate domains and codomains). The Gowers
![]() $U^s$
-norm on a finite abelian group G is then defined via
$U^s$
-norm on a finite abelian group G is then defined via
for
![]() $f\colon G\to\mathbb{C}$
, which is known to be well-defined and a norm for
$f\colon G\to\mathbb{C}$
, which is known to be well-defined and a norm for
![]() $s\ge 2$
and a seminorm for
$s\ge 2$
and a seminorm for
![]() $s=1$
.
$s=1$
.
1·2. Organisation of paper
In Section 2 we prove the main technical result regarding approximating nilsequences as local cubics on Bohr sets. In Section 3 we deduce the main result via a density increment argument. In Appendix A we collect various conventions and definitions regarding nilmanifolds. In Appendix B we essentially reproduce [ Reference Green and Tao13 , appendix A] and note that it verbatim extends to higher degree polynomials. In Appendix C, we manipulate Theorem 1·3 to prove Theorem C·3 which gives correlation with a periodic nilsequence where the underlying nilmanifold has appropriately divisible Lie bracket structure constants. Finally, in Appendix D we collect a number of deferred technical lemmas.
2. Converting nilsequences to local cubics on a Bohr set
The key idea is to work with a presentation of our nilsequence coming from Theorem 1·3, and manipulate it into an approximate form composed of locally cubic functions on Bohr sets.
We will first define Bohr sets formally.
Definition 2·1. Given
![]() $S\subseteq\mathbb{Z}/N\mathbb{Z}$
and
$S\subseteq\mathbb{Z}/N\mathbb{Z}$
and
![]() $\rho\in(0,1)$
, we define the (centered) Bohr set
$\rho\in(0,1)$
, we define the (centered) Bohr set
Given
![]() $\alpha=(\alpha_\xi)_{\xi\in S}\in(\mathbb{R}/\mathbb{Z})^S$
, we define the uncentered Bohr set
$\alpha=(\alpha_\xi)_{\xi\in S}\in(\mathbb{R}/\mathbb{Z})^S$
, we define the uncentered Bohr set
The parameter
![]() $|S|$
is the rank and
$|S|$
is the rank and
![]() $\rho$
is the radius.
$\rho$
is the radius.
We next define the notion of local polynomial structure; we will care specifically about the case of degree
![]() $s=3$
.
$s=3$
.
Definition 2·2. Given
![]() $S\subseteq G$
and
$S\subseteq G$
and
![]() $f\colon S\to H$
, we say that f is locally degree
$f\colon S\to H$
, we say that f is locally degree
![]() $s\ge0$
if for all
$s\ge0$
if for all
![]() $x,h_1,\ldots,h_{s+1}$
such that
$x,h_1,\ldots,h_{s+1}$
such that
![]() $x+\sum_{j=1}^{s+1}\epsilon_jh_j\in S$
for all
$x+\sum_{j=1}^{s+1}\epsilon_jh_j\in S$
for all
![]() $\epsilon=(\epsilon_1,\ldots,\epsilon_{s+1})\in\{0,1\}^{s+1}$
, we have
$\epsilon=(\epsilon_1,\ldots,\epsilon_{s+1})\in\{0,1\}^{s+1}$
, we have
Remark. We will primarily be concerned with
![]() $S\subseteq\mathbb{Z}/N\mathbb{Z}$
and
$S\subseteq\mathbb{Z}/N\mathbb{Z}$
and
![]() $H = \mathbb{R}/\mathbb{Z}$
.
$H = \mathbb{R}/\mathbb{Z}$
.
Proposition 2·3. Suppose we are given a degree 3 nilmanifold
![]() $G/\Gamma$
of dimension d, complexity M, and all Lie bracket structure constants divisible by 12. Furthermore suppose that
$G/\Gamma$
of dimension d, complexity M, and all Lie bracket structure constants divisible by 12. Furthermore suppose that
![]() $F\colon G/\Gamma\to\mathbb{C}$
is smooth with Lipschitz norm bounded by 1 and let
$F\colon G/\Gamma\to\mathbb{C}$
is smooth with Lipschitz norm bounded by 1 and let
![]() $\eta\in(0,1/2)$
.
$\eta\in(0,1/2)$
.
Then there exist data such that
such that:
-
(i)
 $S\subseteq (1/N)\mathbb{Z}$
with size at most
$S\subseteq (1/N)\mathbb{Z}$
with size at most
 $d+1$
;
$d+1$
; -
(ii) I is an index set of size at most
 $O(M \eta^{-1})^{O(d^{O(1)})}$
and
$O(M \eta^{-1})^{O(d^{O(1)})}$
and
 $|w_i|\le O(M \eta^{-1})^{O(d^{O(1)})}$
for all
$|w_i|\le O(M \eta^{-1})^{O(d^{O(1)})}$
for all
 $i\in I$
;
$i\in I$
; -
(iii)
 $y_i\in\mathbb{Z}/N\mathbb{Z}$
for all
$y_i\in\mathbb{Z}/N\mathbb{Z}$
for all
 $i\in I$
;
$i\in I$
; -
(iv)
 $\phi_i\colon\mathbb{Z}/N\mathbb{Z}\to\mathbb{R}/\mathbb{Z}$
is locally cubic on
$\phi_i\colon\mathbb{Z}/N\mathbb{Z}\to\mathbb{R}/\mathbb{Z}$
is locally cubic on
 $y_i + B(S,1/100)$
.
$y_i + B(S,1/100)$
.
Then, Proposition 1·4 directly follows from a slightly modified version of Theorem 1·3 (namely Theorem C·3) and Proposition 2·3. Theorem C·3 allows one to essentially assume that the underlying nilsequence is N-periodic and various structure constants are sufficiently divisible.
Proof of Proposition 1·4. By Theorem C·3, there exists a nilmanifold
![]() $G/\Gamma$
with function F and a polynomial sequence g(n) such that
$G/\Gamma$
with function F and a polynomial sequence g(n) such that
with
![]() $g(0) = \operatorname{id}_G$
and
$g(0) = \operatorname{id}_G$
and
![]() $G/\Gamma$
having dimension d, complexity at most M and all structure constants divisible by 12 with
$G/\Gamma$
having dimension d, complexity at most M and all structure constants divisible by 12 with
We now approximate
![]() $F(g(n)\Gamma)$
by a function H(n) such that
$F(g(n)\Gamma)$
by a function H(n) such that
![]() $\sup_{n\in \mathbb{Z}/N\mathbb{Z}}|F(g(n)\Gamma)-H(n)|\le\eta$
using Proposition 2·3. As f is 1-bounded, we immediately have
$\sup_{n\in \mathbb{Z}/N\mathbb{Z}}|F(g(n)\Gamma)-H(n)|\le\eta$
using Proposition 2·3. As f is 1-bounded, we immediately have
We have some additional guarantees on the structure of H (in particular, some associated data
![]() $S,I,w_i,y_i,\phi_i$
). Applying Pigeonhole on the index set I and using that the
$S,I,w_i,y_i,\phi_i$
). Applying Pigeonhole on the index set I and using that the
![]() $w_i$
are sufficiently bounded, there exist
$w_i$
are sufficiently bounded, there exist
![]() $y\in\mathbb{Z}/N\mathbb{Z}$
, S a set of at most size
$y\in\mathbb{Z}/N\mathbb{Z}$
, S a set of at most size
![]() $d+1$
,
$d+1$
,
![]() $\rho=1/100$
, and
$\rho=1/100$
, and
![]() $\phi\colon\mathbb{Z}/N\mathbb{Z}\to\mathbb{R}/\mathbb{Z}$
locally cubic on
$\phi\colon\mathbb{Z}/N\mathbb{Z}\to\mathbb{R}/\mathbb{Z}$
locally cubic on
![]() $y + B(S,\rho)$
such that
$y + B(S,\rho)$
such that
In order to prove Proposition 2·3, we will need a number of quantitative and structural lemmas about nilsequences. These arguments are deferred to Appendix D. We first require the following quantitative partition of unity for nilmanifolds.
Lemma 2·4. Fix
![]() $\varepsilon\in (0,1/2)$
and a nilmanifold
$\varepsilon\in (0,1/2)$
and a nilmanifold
![]() $G/\Gamma$
of degree s, dimension d, and complexity M. There exists an index set I and a collection of nonnegative smooth functions
$G/\Gamma$
of degree s, dimension d, and complexity M. There exists an index set I and a collection of nonnegative smooth functions
![]() $\tau_j\colon G/\Gamma\to\mathbb{R}$
for
$\tau_j\colon G/\Gamma\to\mathbb{R}$
for
![]() $j\in I$
such that:
$j\in I$
such that:
-
(i)
 $L\;:\!=\; (M/\varepsilon)^{O_s(d^{O_s(1)})}$
;
$L\;:\!=\; (M/\varepsilon)^{O_s(d^{O_s(1)})}$
; -
(ii) for all
 $g\in G$
, we have
$g\in G$
, we have
 $\sum_{j\in I}\tau_j(g\Gamma) = 1$
;
$\sum_{j\in I}\tau_j(g\Gamma) = 1$
; -
(iii)
 $|I|\le L$
;
$|I|\le L$
; -
(vi) for each
 $j\in I$
, there exists
$j\in I$
, there exists
 $\beta\in [\!-\!L,L]^{d}$
so that for any
$\beta\in [\!-\!L,L]^{d}$
so that for any
 $g\Gamma \in \operatorname{supp}(\tau_j)$
there exist
$g\Gamma \in \operatorname{supp}(\tau_j)$
there exist
 $g'\in g\Gamma$
such that
$g'\in g\Gamma$
such that
 $\log_G(g')\in \prod_{i=1}^d[\beta_i-\varepsilon,\beta_i+\varepsilon]$
;
$\log_G(g')\in \prod_{i=1}^d[\beta_i-\varepsilon,\beta_i+\varepsilon]$
; -
(v)
 $\tau_j$
are L-Lipschitz on
$\tau_j$
are L-Lipschitz on
 $G/\Gamma$
.
$G/\Gamma$
.
We also require the algebraic fact that if the Lie bracket structure constants of
![]() $G/\Gamma$
are sufficiently divisible then
$G/\Gamma$
are sufficiently divisible then
![]() $\psi_{\exp}(\Gamma) = \mathbb{Z}^d$
.
$\psi_{\exp}(\Gamma) = \mathbb{Z}^d$
.
Lemma 2·5. There exists an integer
![]() $C_s\ge 1$
such that the following holds. Fix a nilmanifold
$C_s\ge 1$
such that the following holds. Fix a nilmanifold
![]() $G/\Gamma$
of degree s and a Mal’cev basis
$G/\Gamma$
of degree s and a Mal’cev basis
![]() $\mathcal{X}$
such that all Lie bracket structure constants of
$\mathcal{X}$
such that all Lie bracket structure constants of
![]() $G/\Gamma$
are divisible by
$G/\Gamma$
are divisible by
![]() $C_s$
. Then
$C_s$
. Then
![]() $\psi_{\exp}(\Gamma) = \mathbb{Z}^d$
.
$\psi_{\exp}(\Gamma) = \mathbb{Z}^d$
.
Remark. We may take
![]() $C_3 = 12$
.
$C_3 = 12$
.
Next we need the conversion between the nilmanifold distance and distance in coordinates of the first kind (on
![]() $\mathbb{R}^d$
).
$\mathbb{R}^d$
).
Lemma 2·6. Fix a nilmanifold
![]() $G/\Gamma$
of degree s, dimension d, and complexity M. If
$G/\Gamma$
of degree s, dimension d, and complexity M. If
![]() $\lVert\psi_{\exp}(x) - \psi_{\exp}(y)\rVert_\infty\le\varepsilon$
and
$\lVert\psi_{\exp}(x) - \psi_{\exp}(y)\rVert_\infty\le\varepsilon$
and
![]() $\lVert\psi_{\exp}(x)\rVert_\infty\le L$
then
$\lVert\psi_{\exp}(x)\rVert_\infty\le L$
then
We also require the following basic estimate regarding Fourier expansion of Lipschitz functions on the torus; this follows immediately by quantifying the proof in [ Reference Tao36 , proposition 1·1·13] (see e.g. [ Reference Peluse, Sah and Sawhney26 , lemma A·8]).
Lemma 2·7. Fix
![]() $0 \lt \varepsilon \lt 1/2$
, and let
$0 \lt \varepsilon \lt 1/2$
, and let
![]() $F\colon(\mathbb{R}/\mathbb{Z})^d\to\mathbb{C}$
with
$F\colon(\mathbb{R}/\mathbb{Z})^d\to\mathbb{C}$
with
![]() $\lVert F\rVert_{\mathrm{Lip}}\le L$
with metric
$\lVert F\rVert_{\mathrm{Lip}}\le L$
with metric
![]() $d(x,y) = \max_{1\le i\le d}\lVert x_i-y_i\rVert_{\mathbb{R}/\mathbb{Z}}$
for
$d(x,y) = \max_{1\le i\le d}\lVert x_i-y_i\rVert_{\mathbb{R}/\mathbb{Z}}$
for
![]() $x,y\in (\mathbb{R}/\mathbb{Z})^d$
. There exists an absolute constant
$x,y\in (\mathbb{R}/\mathbb{Z})^d$
. There exists an absolute constant
![]() $C \gt 0$
such that there exist
$C \gt 0$
such that there exist
![]() $c_{\xi}$
with
$c_{\xi}$
with
![]() $\sum_{\xi}|c_{\xi}|\le (3CLd\varepsilon^{-1})^{5d}$
and
$\sum_{\xi}|c_{\xi}|\le (3CLd\varepsilon^{-1})^{5d}$
and
 \[\sup_{x\in (\mathbb{R}/\mathbb{Z})^d}\bigg|F(x) - \sum_{|\xi|\le (CLd\varepsilon^{-1})^{2}}c_{\xi}e(\xi\cdot x)\bigg|\le \varepsilon.\]
\[\sup_{x\in (\mathbb{R}/\mathbb{Z})^d}\bigg|F(x) - \sum_{|\xi|\le (CLd\varepsilon^{-1})^{2}}c_{\xi}e(\xi\cdot x)\bigg|\le \varepsilon.\]
We finally require the following elementary lemma regarding how local degree acts with respect to multiplication; this is once again deferred to Appendix D. (Recall we are defining local degree with respect to
![]() $\partial$
as opposed to
$\partial$
as opposed to
![]() $\Delta$
, and the following cannot be altered to only require that the functions reduced
$\Delta$
, and the following cannot be altered to only require that the functions reduced
![]() $\mathrm{mod}\;1$
have local degree.)
$\mathrm{mod}\;1$
have local degree.)
Lemma 2·8. If
![]() $S\subseteq G$
and
$S\subseteq G$
and
![]() $f_j\colon S\to\mathbb{C}$
are locally degree
$f_j\colon S\to\mathbb{C}$
are locally degree
![]() $d_j$
functions, then
$d_j$
functions, then
![]() $g=\prod_{j=1}^kf_k$
is a locally degree
$g=\prod_{j=1}^kf_k$
is a locally degree
![]() $\sum_{j=1}^kd_j$
function.
$\sum_{j=1}^kd_j$
function.
We are ready to proceed.
Proof of Proposition 2·3. We break the proof into a series of steps.
Step 1. Polynomial sequence and group multiplication in coordinates. Note that as we are dealing with nilpotent groups of step at most 3 we have
by the Baker–Campbell–Hausdorff formula. Let
![]() $d_j=\dim G_{1}-\dim G_{j+1}$
and let our Mal’cev basis be
$d_j=\dim G_{1}-\dim G_{j+1}$
and let our Mal’cev basis be
![]() $(X_k)_{k\in[d]}$
such that
$(X_k)_{k\in[d]}$
such that
![]() $(X_k)_{k \gt d_j}$
spans
$(X_k)_{k \gt d_j}$
spans
![]() $\log G_{j+1}$
for
$\log G_{j+1}$
for
![]() $j\in\{0,1,2\}$
. Note that by definition
$j\in\{0,1,2\}$
. Note that by definition
![]() $\Gamma$
is the set of elements of the form
$\Gamma$
is the set of elements of the form
![]() $\prod_{i=1}^{d}\exp\!(t_iX_i)$
for
$\prod_{i=1}^{d}\exp\!(t_iX_i)$
for
![]() $t_i\in\mathbb{Z}$
. Recall that we have
$t_i\in\mathbb{Z}$
. Recall that we have
 \[[X_i,X_j]=\sum_{k=1}^dc_{ijk}X_k\]
\[[X_i,X_j]=\sum_{k=1}^dc_{ijk}X_k\]
for
![]() $c_{ijk}$
integers divisible by 12 and of absolute value at most M due to the complexity assumption. As
$c_{ijk}$
integers divisible by 12 and of absolute value at most M due to the complexity assumption. As
![]() $[\log G_i, \log G_j]\subseteq \log G_{i+j}$
, we have that
$[\log G_i, \log G_j]\subseteq \log G_{i+j}$
, we have that
![]() $c_{ijk}=0$
for
$c_{ijk}=0$
for
![]() $k\le d_{a+b+1}$
if
$k\le d_{a+b+1}$
if
![]() $i \gt d_a$
and
$i \gt d_a$
and
![]() $j \gt d_b$
.
$j \gt d_b$
.
As g(n) is a polynomial sequence with
![]() $g(0) = \operatorname{id}_G$
, by Taylor expansion we have
$g(0) = \operatorname{id}_G$
, by Taylor expansion we have
with
![]() $g_i\in G_i$
. Therefore
$g_i\in G_i$
. Therefore
 \begin{align*}\log\!(g(n)) &= \log\!\bigg(\!\exp\!(n\log\!(g_1))\exp\bigg(\binom{n}{2}\log\!(g_2)\bigg)\exp\bigg(\binom{n}{3}\log\!(g_3)\bigg)\bigg)\\&=n\log\!(g_1) + \binom{n}{2}\log\!(g_2) + \frac{n}{2}\binom{n}{2}[\log\!(g_1),\log\!(g_2)] + \binom{n}{3}\log\!(g_3)\end{align*}
\begin{align*}\log\!(g(n)) &= \log\!\bigg(\!\exp\!(n\log\!(g_1))\exp\bigg(\binom{n}{2}\log\!(g_2)\bigg)\exp\bigg(\binom{n}{3}\log\!(g_3)\bigg)\bigg)\\&=n\log\!(g_1) + \binom{n}{2}\log\!(g_2) + \frac{n}{2}\binom{n}{2}[\log\!(g_1),\log\!(g_2)] + \binom{n}{3}\log\!(g_3)\end{align*}
with
![]() $[\log\!(g_1),\log\!(g_2)]\in\log\!(G_3)$
. Therefore we have
$[\log\!(g_1),\log\!(g_2)]\in\log\!(G_3)$
. Therefore we have
 \begin{equation}g(n)=\exp\!\bigg(\sum_{j=1}^{d}p_j(n)X_j\bigg)\end{equation}
\begin{equation}g(n)=\exp\!\bigg(\sum_{j=1}^{d}p_j(n)X_j\bigg)\end{equation}
with
![]() $p_j(0) = 0$
and
$p_j(0) = 0$
and
![]() $p_j$
being at most degree 1 if
$p_j$
being at most degree 1 if
![]() $1\le j\le d_1$
, at most degree 2 if
$1\le j\le d_1$
, at most degree 2 if
![]() $d_1+1\le j\le d_2$
, and at most degree 3 if
$d_1+1\le j\le d_2$
, and at most degree 3 if
![]() $d_2+1\le j\le d_3=d$
. We next realise multiplication of two elements corresponding to Mal’cev coordinates of the first kind as
$d_2+1\le j\le d_3=d$
. We next realise multiplication of two elements corresponding to Mal’cev coordinates of the first kind as
 \begin{align*}&(x_1,\ldots,x_d)\ast(y_1,\ldots,y_d)\\&=(x_1+y_1,\ldots,x_{d_1}+y_{d_1},x_{d_1+1}+y_{d_1+1}+\phi_{d_1+1}(x_{\le d_1},y_{\le d_1}),\ldots,x_{d_2}+y_{d_2}\\&+\phi_{d_2}(x_{\le d_1},y_{\le d_1}), x_{d_2+1}+y_{d_2+1}+\phi_{d_2+1}(x_{\le d_2},y_{\le d_2})+\varphi_{d_2+1}(x_{\le d_1},y_{\le d_1}),\ldots,x_d+y_d\\&+\phi_d(x_{\le d},y_{\le d})+\varphi_d(x_{\le d_1},y_{\le d_1}))\end{align*}
\begin{align*}&(x_1,\ldots,x_d)\ast(y_1,\ldots,y_d)\\&=(x_1+y_1,\ldots,x_{d_1}+y_{d_1},x_{d_1+1}+y_{d_1+1}+\phi_{d_1+1}(x_{\le d_1},y_{\le d_1}),\ldots,x_{d_2}+y_{d_2}\\&+\phi_{d_2}(x_{\le d_1},y_{\le d_1}), x_{d_2+1}+y_{d_2+1}+\phi_{d_2+1}(x_{\le d_2},y_{\le d_2})+\varphi_{d_2+1}(x_{\le d_1},y_{\le d_1}),\ldots,x_d+y_d\\&+\phi_d(x_{\le d},y_{\le d})+\varphi_d(x_{\le d_1},y_{\le d_1}))\end{align*}
where
![]() $\phi_j$
are bilinear forms with integral coefficients and
$\phi_j$
are bilinear forms with integral coefficients and
![]() $\varphi_j$
are cubic forms with integral coefficients. This is an immediate consequence of the Baker–Campbell–Hausdorff formula and using the assumption that the Lie bracket structure constants are all divisible by 12. Furthermore these coefficients are of height at most
$\varphi_j$
are cubic forms with integral coefficients. This is an immediate consequence of the Baker–Campbell–Hausdorff formula and using the assumption that the Lie bracket structure constants are all divisible by 12. Furthermore these coefficients are of height at most
![]() $O(Md)^{O(1)}$
and since
$O(Md)^{O(1)}$
and since
![]() $[G_2,G_2]\subseteq G_4=\operatorname{Id}_G$
, the bilinear form
$[G_2,G_2]\subseteq G_4=\operatorname{Id}_G$
, the bilinear form
![]() $\phi_j$
for
$\phi_j$
for
![]() $j\in[d_1+1,d_2]$
has all coordinates 0 on the box
$j\in[d_1+1,d_2]$
has all coordinates 0 on the box
![]() $[d_1+1,d_2]^2$
.
$[d_1+1,d_2]^2$
.
Step 2. Explicit representation of nilsequence with coordinates. We can represent the coordinates of
![]() $g(n)\Gamma$
in a fundamental domain with respect to Mal’cev coordinates of the first kind via iterated floor and fractional parts. These coordinates are not smooth at the boundary and thus we decompose F via a partition of unity (and using different fundamental domains for each part). This will allow us to manipulate such coordinate functions without needing to worry very precisely about the minor discontinuities.
$g(n)\Gamma$
in a fundamental domain with respect to Mal’cev coordinates of the first kind via iterated floor and fractional parts. These coordinates are not smooth at the boundary and thus we decompose F via a partition of unity (and using different fundamental domains for each part). This will allow us to manipulate such coordinate functions without needing to worry very precisely about the minor discontinuities.
Let
![]() $L = O(M)^{O(d^{O(1)})}$
. We write
$L = O(M)^{O(d^{O(1)})}$
. We write
with
![]() $F_i=F\tau_i$
where
$F_i=F\tau_i$
where
![]() $\tau_i$
is as in Lemma 2·4 applied with parameter
$\tau_i$
is as in Lemma 2·4 applied with parameter
![]() $\varepsilon=10^{-3}$
. This will allow us to represent
$\varepsilon=10^{-3}$
. This will allow us to represent
![]() $F\tau_i$
on the fundamental domain (with respect to Mal’cev coordinates of the first kind)
$F\tau_i$
on the fundamental domain (with respect to Mal’cev coordinates of the first kind)
![]() $\prod_{j=1}^d[\beta_j^{(i)}-1/2,\beta_j^{(i)}+1/2)$
, where
$\prod_{j=1}^d[\beta_j^{(i)}-1/2,\beta_j^{(i)}+1/2)$
, where
![]() $\beta^{(i)}\in [\!-\!L,L]^{d}$
and
$\beta^{(i)}\in [\!-\!L,L]^{d}$
and
 \[\operatorname{supp}(F\tau_i)\subseteq\operatorname{supp}(\tau_i)\subseteq\prod_{j=1}^d[\beta_j^{(i)}-10^{-3},\beta_j^{(i)}+10^{-3}).\]
\[\operatorname{supp}(F\tau_i)\subseteq\operatorname{supp}(\tau_i)\subseteq\prod_{j=1}^d[\beta_j^{(i)}-10^{-3},\beta_j^{(i)}+10^{-3}).\]
We now define nonstandard (shifted) floor and fractional part functions for each
![]() $i\in I$
and
$i\in I$
and
![]() $j\in[d]$
so that
$j\in[d]$
so that
 \begin{align*}\{t\}_{i,j} &\equiv t \;\mathrm{mod}\;1\\t &= \{t\}_{i,j} + \lfloor t\rfloor_{i,j}\\\{t\}_{i,j}&\in [\beta_j^{(i)}-1/2,\beta_j^{(i)}+1/2).\end{align*}
\begin{align*}\{t\}_{i,j} &\equiv t \;\mathrm{mod}\;1\\t &= \{t\}_{i,j} + \lfloor t\rfloor_{i,j}\\\{t\}_{i,j}&\in [\beta_j^{(i)}-1/2,\beta_j^{(i)}+1/2).\end{align*}
For nearly the entire remainder of the proof, we will focus on massaging the representation of
![]() $F_i(x)$
into a more convenient form. Given
$F_i(x)$
into a more convenient form. Given
![]() $x\in G$
such that
$x\in G$
such that
![]() $\psi_{\exp}(x)= (x_1,\ldots,x_d)$
, consider
$\psi_{\exp}(x)= (x_1,\ldots,x_d)$
, consider
![]() $\gamma$
with Mal’cev coordinates of the first kind:
$\gamma$
with Mal’cev coordinates of the first kind:
where
![]() $x_{\le d_2}^\ast$
has coordinates equal to those on the first line of (2·2) (so it implicitly depends on i) and
$x_{\le d_2}^\ast$
has coordinates equal to those on the first line of (2·2) (so it implicitly depends on i) and
![]() $\lfloor x_{\le d_1}\rfloor_i = (\lfloor x_1\rfloor_{i,1},\ldots, \lfloor x_1\rfloor_{i,d_1})$
. Furthermore let
$\lfloor x_{\le d_1}\rfloor_i = (\lfloor x_1\rfloor_{i,1},\ldots, \lfloor x_1\rfloor_{i,d_1})$
. Furthermore let
![]() $\{x_{\le d_1}\}_i = x - \lfloor x_{\le d_1}\rfloor_i$
. Note that
$\{x_{\le d_1}\}_i = x - \lfloor x_{\le d_1}\rfloor_i$
. Note that
![]() $\gamma\in \Gamma$
by Lemma 2·5.
$\gamma\in \Gamma$
by Lemma 2·5.
Thus
![]() $x\gamma$
has coordinates
$x\gamma$
has coordinates
which is in the specified fundamental domain
![]() $\prod_{j=1}^d[\beta_j^{(i)}-1/2,\beta_j^{(i)}+1/2)$
for
$\prod_{j=1}^d[\beta_j^{(i)}-1/2,\beta_j^{(i)}+1/2)$
for
![]() $F_i$
. Recall also that
$F_i$
. Recall also that
![]() $\phi_j$
for
$\phi_j$
for
![]() $j\in[d_2+1,d]$
has certain 0 coefficients.
$j\in[d_2+1,d]$
has certain 0 coefficients.
Let
![]() $x^{\ast}_{[d_1+1,d_2]}$
denote the vector with
$x^{\ast}_{[d_1+1,d_2]}$
denote the vector with
![]() $d_2$
coordinates, the first
$d_2$
coordinates, the first
![]() $d_1$
of which are zero and the last
$d_1$
of which are zero and the last
![]() $d_2-d_1$
of which are
$d_2-d_1$
of which are
![]() $(\!-\lfloor x_j+\phi_j(x_{\le d_1},-\lfloor x_{\le d_1}\rfloor_i)\rfloor_{i,j})_{d_1+1\le j\le d_2}$
. Let
$(\!-\lfloor x_j+\phi_j(x_{\le d_1},-\lfloor x_{\le d_1}\rfloor_i)\rfloor_{i,j})_{d_1+1\le j\le d_2}$
. Let
![]() $y_j = x_j+\phi_j(x_{\le d_1},-\lfloor x_{\le d_1}\rfloor_i)$
,
$y_j = x_j+\phi_j(x_{\le d_1},-\lfloor x_{\le d_1}\rfloor_i)$
,
![]() $y^{\ast}_{[d_1+1,d_2]}$
analogously be a vector of these coordinates and
$y^{\ast}_{[d_1+1,d_2]}$
analogously be a vector of these coordinates and
![]() $d_1$
many 0s, and let
$d_1$
many 0s, and let
![]() $\{y_{[d_1+1,d_2]}\}_i^\ast = (0,\ldots,0,\{y_{d_1+1}\}_{i,d_1+1},\ldots,\{y_{d_2}\}_{i,d_2})$
.
$\{y_{[d_1+1,d_2]}\}_i^\ast = (0,\ldots,0,\{y_{d_1+1}\}_{i,d_1+1},\ldots,\{y_{d_2}\}_{i,d_2})$
.
Note that we have the identity
where the subscripts 1 and 2 indicate potentially different shift types. Therefore
 \begin{align*}\phi_j(x_{\le d_2},x_{\le d_2}^\ast) &= \phi_j(x_{\le d_2},-\lfloor x_{\le d_1}\rfloor_i) + \phi_j(x_{\le d_2},x^{\ast}_{[d_1+1,d_2]})\\&= \phi_j(x_{\le d_2},-\lfloor x_{\le d_1}\rfloor_i) + \phi_j(x_{\le d_1},x^{\ast}_{[d_1+1,d_2]})\\&= \phi_j(x_{\le d_2},-\lfloor x_{\le d_1}\rfloor_i) + \phi_j(\lfloor x_{\le d_1}\rfloor_i,y^{\ast}_{[d_1+1,d_2]})-\phi_j(x_{\le d_1},y^{\ast}_{[d_1+1,d_2]}) \\&\qquad\qquad+ \phi_j(\lfloor x_{\le d_1}\rfloor_i, x^{\ast}_{[d_1+1,d_2]})+ \phi_j(\{x_{\le d_1}\}_i,\{y_{[d_1+1,d_2]}\}_i^\ast).\end{align*}
\begin{align*}\phi_j(x_{\le d_2},x_{\le d_2}^\ast) &= \phi_j(x_{\le d_2},-\lfloor x_{\le d_1}\rfloor_i) + \phi_j(x_{\le d_2},x^{\ast}_{[d_1+1,d_2]})\\&= \phi_j(x_{\le d_2},-\lfloor x_{\le d_1}\rfloor_i) + \phi_j(x_{\le d_1},x^{\ast}_{[d_1+1,d_2]})\\&= \phi_j(x_{\le d_2},-\lfloor x_{\le d_1}\rfloor_i) + \phi_j(\lfloor x_{\le d_1}\rfloor_i,y^{\ast}_{[d_1+1,d_2]})-\phi_j(x_{\le d_1},y^{\ast}_{[d_1+1,d_2]}) \\&\qquad\qquad+ \phi_j(\lfloor x_{\le d_1}\rfloor_i, x^{\ast}_{[d_1+1,d_2]})+ \phi_j(\{x_{\le d_1}\}_i,\{y_{[d_1+1,d_2]}\}_i^\ast).\end{align*}
The equality
![]() $\phi_j(x_{\le d_2},x^{\ast}_{[d_1+1,d_2]}) = \phi_j(x_{\le d_1},x^{\ast}_{[d_1+1,d_2]})$
follows as
$\phi_j(x_{\le d_2},x^{\ast}_{[d_1+1,d_2]}) = \phi_j(x_{\le d_1},x^{\ast}_{[d_1+1,d_2]})$
follows as
![]() $\phi_j$
has no nonzero coordinates on the box
$\phi_j$
has no nonzero coordinates on the box
![]() $[d_1+1,d_2]^2$
.
$[d_1+1,d_2]^2$
.
This implies that
 \begin{align*}&(\{x_j+\varphi_j(x_{\le d_1},-\lfloor x_{\le d_1}\rfloor_i)+\phi_j(x_{\le d_2},x_{\le d_2}^\ast)\}_{i,j})_{d_2+1\le j\le d}\\&= (\{x_j+\varphi_j(x_{\le d_1},-\lfloor x_{\le d_1}\rfloor_i)+\phi_j(x_{\le d_2},-\lfloor x_{\le d_1}\rfloor_i) + \phi_j(\lfloor x_{\le d_1}\rfloor_i,y^{\ast}_{[d_1+1,d_2]})\\&\qquad-\phi_j(x_{\le d_1},y^{\ast}_{[d_1+1,d_2]})+ \phi_j(\{x_{\le d_1}\}_i,\{y_{[d_1+1,d_2]}\}_i^\ast)\}_{i,j})_{d_2+1\le j\le d};\end{align*}
\begin{align*}&(\{x_j+\varphi_j(x_{\le d_1},-\lfloor x_{\le d_1}\rfloor_i)+\phi_j(x_{\le d_2},x_{\le d_2}^\ast)\}_{i,j})_{d_2+1\le j\le d}\\&= (\{x_j+\varphi_j(x_{\le d_1},-\lfloor x_{\le d_1}\rfloor_i)+\phi_j(x_{\le d_2},-\lfloor x_{\le d_1}\rfloor_i) + \phi_j(\lfloor x_{\le d_1}\rfloor_i,y^{\ast}_{[d_1+1,d_2]})\\&\qquad-\phi_j(x_{\le d_1},y^{\ast}_{[d_1+1,d_2]})+ \phi_j(\{x_{\le d_1}\}_i,\{y_{[d_1+1,d_2]}\}_i^\ast)\}_{i,j})_{d_2+1\le j\le d};\end{align*}
we are able to drop
![]() $\phi_j(\lfloor x_{\le d_1}\rfloor_i, x^{\ast}_{[d_1+1,d_2]})$
as
$\phi_j(\lfloor x_{\le d_1}\rfloor_i, x^{\ast}_{[d_1+1,d_2]})$
as
![]() $\phi_j$
has integral coefficients and we are taking fractional parts. Using the above general identity and this expression, we thus have coordinates of the form
$\phi_j$
has integral coefficients and we are taking fractional parts. Using the above general identity and this expression, we thus have coordinates of the form
 \begin{align}&(\{x_j\}_{i,j})_{j\in[d_1]},\quad(\{x_j-\phi_j(x_{\le d_1},\lfloor x_{\le d_1}\rfloor_i)\}_{i,j})_{d_1+1\le j\le d_2},\notag\\&(\{x_j+\varphi_j^\ast(x_{\le d_1},\lfloor x_{\le d_1}\rfloor_i)+\phi_j^\ast(x_{\le d_2},\lfloor x_{\le d_1}\rfloor_i)\nonumber\\ &\quad +\sigma_j(x_{\le d_2},x_{\le d_1})+\phi_j(\{x_{\le d_1}\}_i,\{y_{[d_1+1,d_2]}\}^{\ast})\}_{i,j})_{d_2+1\le j\le d_3}.\end{align}
\begin{align}&(\{x_j\}_{i,j})_{j\in[d_1]},\quad(\{x_j-\phi_j(x_{\le d_1},\lfloor x_{\le d_1}\rfloor_i)\}_{i,j})_{d_1+1\le j\le d_2},\notag\\&(\{x_j+\varphi_j^\ast(x_{\le d_1},\lfloor x_{\le d_1}\rfloor_i)+\phi_j^\ast(x_{\le d_2},\lfloor x_{\le d_1}\rfloor_i)\nonumber\\ &\quad +\sigma_j(x_{\le d_2},x_{\le d_1})+\phi_j(\{x_{\le d_1}\}_i,\{y_{[d_1+1,d_2]}\}^{\ast})\}_{i,j})_{d_2+1\le j\le d_3}.\end{align}
Here
![]() $\varphi_j^{\ast}$
are degree at most 3 polynomials and
$\varphi_j^{\ast}$
are degree at most 3 polynomials and
![]() $\phi_j^{\ast},\sigma_j$
are bilinear forms. Additionally, all coefficients are integral with heights bounded by
$\phi_j^{\ast},\sigma_j$
are bilinear forms. Additionally, all coefficients are integral with heights bounded by
![]() $(O(Md))^{O(1)}$
.
$(O(Md))^{O(1)}$
.
Let us briefly take stock of what has been accomplished in the last manipulation. Note that there are no longer any “iterated” floor expressions and the only terms being “floored” are
![]() $x_{\le d_1}$
. The Bohr sets we will ultimately take therefore are determined by these coordinates only.
$x_{\le d_1}$
. The Bohr sets we will ultimately take therefore are determined by these coordinates only.
We now “lift”
![]() $F_i$
from a function on
$F_i$
from a function on
![]() $G/\Gamma$
to
$G/\Gamma$
to
![]() $\widetilde{F}_i$
on
$\widetilde{F}_i$
on
![]() $(\mathbb{R}/\mathbb{Z})^d$
. This can be done via identifying
$(\mathbb{R}/\mathbb{Z})^d$
. This can be done via identifying
![]() $(\mathbb{R}/\mathbb{Z})^d$
with the fundamental domain
$(\mathbb{R}/\mathbb{Z})^d$
with the fundamental domain
![]() $\prod_{j=1}^d[\beta_j^{(i)}-1/2,\beta_j^{(i)}+1/2)$
with respect to
$\prod_{j=1}^d[\beta_j^{(i)}-1/2,\beta_j^{(i)}+1/2)$
with respect to
![]() $\psi_{\exp}$
. Now,
$\psi_{\exp}$
. Now,
![]() $\widetilde{F}_i$
is seen to be
$\widetilde{F}_i$
is seen to be
![]() $O(LM/\varepsilon)^{O(d^{O(1)})}$
-Lipschitz on
$O(LM/\varepsilon)^{O(d^{O(1)})}$
-Lipschitz on
![]() $(\mathbb{R}/\mathbb{Z})^d$
by Lemma 2·6. (We are also using that the support of
$(\mathbb{R}/\mathbb{Z})^d$
by Lemma 2·6. (We are also using that the support of
![]() $\widetilde{F}_i$
is close to the center of the torus, so the torus metric and
$\widetilde{F}_i$
is close to the center of the torus, so the torus metric and
![]() $\ell^\infty$
on
$\ell^\infty$
on
![]() $\mathbb{R}^d$
are the same where it matters.)
$\mathbb{R}^d$
are the same where it matters.)
Therefore it is sufficient to consider
![]() $\widetilde{F}_i$
with coordinates given by
$\widetilde{F}_i$
with coordinates given by
 \begin{align}&(x_j)_{j\in[d_1]},\quad(x_j-\phi_j(x_{\le d_1},\lfloor x_{\le d_1}\rfloor_i))_{d_1+1\le j\le d_2},\notag\\&(x_j+\varphi_j^\ast(x_{\le d_1},\lfloor x_{\le d_1}\rfloor_i)+\phi_j^\ast(x_{\le d_2},\lfloor x_{\le d_1}\rfloor_i)+\sigma_j(x_{\le d_2},x_{\le d_1})\nonumber \\&+\phi_j(\{x_{\le d_1}\}_i,\{y_{[d_1+1,d_2]}\}_i^\ast))_{d_2+1\le j\le d_3}\end{align}
\begin{align}&(x_j)_{j\in[d_1]},\quad(x_j-\phi_j(x_{\le d_1},\lfloor x_{\le d_1}\rfloor_i))_{d_1+1\le j\le d_2},\notag\\&(x_j+\varphi_j^\ast(x_{\le d_1},\lfloor x_{\le d_1}\rfloor_i)+\phi_j^\ast(x_{\le d_2},\lfloor x_{\le d_1}\rfloor_i)+\sigma_j(x_{\le d_2},x_{\le d_1})\nonumber \\&+\phi_j(\{x_{\le d_1}\}_i,\{y_{[d_1+1,d_2]}\}_i^\ast))_{d_2+1\le j\le d_3}\end{align}
which live on the torus.
We now “smooth”
![]() $\{x_{\le d_1}\}_i$
and
$\{x_{\le d_1}\}_i$
and
![]() $\{y_{[d_1+1,d_2]}\}_i^\ast$
. We replace
$\{y_{[d_1+1,d_2]}\}_i^\ast$
. We replace
![]() $\{\cdot\}_{i,j}$
with a 1-periodic function
$\{\cdot\}_{i,j}$
with a 1-periodic function
![]() $\{\cdot\}_{i,j,\mathrm{sm}}$
which agrees with
$\{\cdot\}_{i,j,\mathrm{sm}}$
which agrees with
![]() $\{x\}_{i,j}$
if
$\{x\}_{i,j}$
if
![]() $\{x\}_{i,j}\in [\beta_j^{(i)}-1/4,\beta_j^{(i)}+1/4)$
and is O(1)-Lipschitz when viewed as a function on
$\{x\}_{i,j}\in [\beta_j^{(i)}-1/4,\beta_j^{(i)}+1/4)$
and is O(1)-Lipschitz when viewed as a function on
![]() $\mathbb{R}/\mathbb{Z}$
. Given this we write
$\mathbb{R}/\mathbb{Z}$
. Given this we write
![]() $\{x_{\le d_1}\}_{\mathrm{sm}}$
and
$\{x_{\le d_1}\}_{\mathrm{sm}}$
and
![]() $\{y_{[d_1+1,d_2]}\}_{\mathrm{sm}}^\ast$
for the associated vectors where smooth fractional parts have been used.
$\{y_{[d_1+1,d_2]}\}_{\mathrm{sm}}^\ast$
for the associated vectors where smooth fractional parts have been used.
We claim that it suffices to consider
![]() $\widetilde{F}_i$
with coordinates given by
$\widetilde{F}_i$
with coordinates given by
 \begin{align}&(x_j)_{j\in[d_1]},\quad(x_j-\phi_j(x_{\le d_1},\lfloor x_{\le d_1}\rfloor_i))_{d_1+1\le j\le d_2},\notag\\&(x_j+\varphi_j^\ast(x_{\le d_1},\lfloor x_{\le d_1}\rfloor_i)+\phi_j^\ast(x_{\le d_2},\lfloor x_{\le d_1}\rfloor_i)+\sigma_j(x_{\le d_2},x_{\le d_1})\nonumber \\ &\quad +\phi_j(\{x_{\le d_1}\}_{\mathrm{sm}},\{y_{[d_1+1,d_2]}\}_{\mathrm{sm}}^\ast))_{d_2+1\le j\le d_3}.\end{align}
\begin{align}&(x_j)_{j\in[d_1]},\quad(x_j-\phi_j(x_{\le d_1},\lfloor x_{\le d_1}\rfloor_i))_{d_1+1\le j\le d_2},\notag\\&(x_j+\varphi_j^\ast(x_{\le d_1},\lfloor x_{\le d_1}\rfloor_i)+\phi_j^\ast(x_{\le d_2},\lfloor x_{\le d_1}\rfloor_i)+\sigma_j(x_{\le d_2},x_{\le d_1})\nonumber \\ &\quad +\phi_j(\{x_{\le d_1}\}_{\mathrm{sm}},\{y_{[d_1+1,d_2]}\}_{\mathrm{sm}}^\ast))_{d_2+1\le j\le d_3}.\end{align}
Note that if
![]() $\{x_{\le d_1}\}_{\mathrm{sm}}\neq\{x_{\le d_1}\}_i$
or
$\{x_{\le d_1}\}_{\mathrm{sm}}\neq\{x_{\le d_1}\}_i$
or
![]() $\{y_{[d_1+1,d_2]}\}_{\mathrm{sm}}\neq\{y_{[d_1+1,d_2]}\}_i^\ast$
we immediately see that one of the coordinates in the first two lines has been forced outside the support of
$\{y_{[d_1+1,d_2]}\}_{\mathrm{sm}}\neq\{y_{[d_1+1,d_2]}\}_i^\ast$
we immediately see that one of the coordinates in the first two lines has been forced outside the support of
![]() $\widetilde{F}_i$
and thus the value is already by construction zero in both coordinates. Otherwise the coordinates in (2·5) and (2·6) match and the representation has been unchanged.
$\widetilde{F}_i$
and thus the value is already by construction zero in both coordinates. Otherwise the coordinates in (2·5) and (2·6) match and the representation has been unchanged.
Step 3. Fourier expansion of nilsequence. Now,
![]() $\widetilde{F}_i\colon(\mathbb{R}/\mathbb{Z})^d\to\mathbb{C}$
is a Lipschitz function. Therefore by Lemma 2·7 with parameter
$\widetilde{F}_i\colon(\mathbb{R}/\mathbb{Z})^d\to\mathbb{C}$
is a Lipschitz function. Therefore by Lemma 2·7 with parameter
![]() $\tau$
,
$\tau$
,
 \[\sup_{z\in (\mathbb{R}/\mathbb{Z})^d}\bigg|\widetilde{F}_i(z) - \sum_{|\xi|\le O(M\tau^{-1})^{O(d^{O(1)})}}c_{\xi} e(\xi\cdot z)\bigg|\le \tau\]
\[\sup_{z\in (\mathbb{R}/\mathbb{Z})^d}\bigg|\widetilde{F}_i(z) - \sum_{|\xi|\le O(M\tau^{-1})^{O(d^{O(1)})}}c_{\xi} e(\xi\cdot z)\bigg|\le \tau\]
with
![]() $|c_{\xi}|\le O(M\tau^{-1})^{O(d^{O(1)})}$
.
$|c_{\xi}|\le O(M\tau^{-1})^{O(d^{O(1)})}$
.
Using this Fourier representation, we have
 \begin{align*}&\sup_{x\in G}\bigg|F_i(x\Gamma) - \sum_{|\xi|\le O(M\tau^{-1})^{O(d^{O(1)})}}c_{\xi} e\bigg(\sum_{j=1}^{d}T_{\xi,j}x_j + \widetilde{\varphi}_{\xi}(x_{\le d_1},\lfloor x_{\le d_1}\rfloor_i)+ \widetilde{\phi}_{\xi}(x_{\le d_2},\lfloor x_{\le d_1}\rfloor_i) \\&\qquad\qquad\qquad\qquad\qquad\qquad\qquad+\widetilde{\sigma}_\xi(x_{\le d_1},x_{\le d_2})+ \widetilde{\phi}'_{\xi}(\{x_{\le d_1}\}_{\mathrm{sm}},\{y_{[d_1+1,d_2]}\}_{\mathrm{sm}}^\ast) \bigg) \bigg|\le \tau\end{align*}
\begin{align*}&\sup_{x\in G}\bigg|F_i(x\Gamma) - \sum_{|\xi|\le O(M\tau^{-1})^{O(d^{O(1)})}}c_{\xi} e\bigg(\sum_{j=1}^{d}T_{\xi,j}x_j + \widetilde{\varphi}_{\xi}(x_{\le d_1},\lfloor x_{\le d_1}\rfloor_i)+ \widetilde{\phi}_{\xi}(x_{\le d_2},\lfloor x_{\le d_1}\rfloor_i) \\&\qquad\qquad\qquad\qquad\qquad\qquad\qquad+\widetilde{\sigma}_\xi(x_{\le d_1},x_{\le d_2})+ \widetilde{\phi}'_{\xi}(\{x_{\le d_1}\}_{\mathrm{sm}},\{y_{[d_1+1,d_2]}\}_{\mathrm{sm}}^\ast) \bigg) \bigg|\le \tau\end{align*}
such that
![]() $\widetilde{\varphi}_\xi$
is at most a degree 3 polynomial, and
$\widetilde{\varphi}_\xi$
is at most a degree 3 polynomial, and
![]() $\widetilde{\phi}_\xi,\widetilde{\sigma}_\xi,\widetilde{\phi}'_\xi$
are bilinear forms. Furthermore all coefficients involved are integers bounded by
$\widetilde{\phi}_\xi,\widetilde{\sigma}_\xi,\widetilde{\phi}'_\xi$
are bilinear forms. Furthermore all coefficients involved are integers bounded by
![]() $(M\tau^{-1})^{O(d^{O(1)})}$
.
$(M\tau^{-1})^{O(d^{O(1)})}$
.
The final smoothing we perform before we specialise to the polynomial sequence under consideration is to remove the
![]() $\{\cdot\}_{\mathrm{sm}}\{\cdot\}_{\mathrm{sm}}$
terms. Note that the function
$\{\cdot\}_{\mathrm{sm}}\{\cdot\}_{\mathrm{sm}}$
terms. Note that the function
is
![]() $O(T L^{O(1)})$
-Lipschitz. We apply Lemma 2·7 with
$O(T L^{O(1)})$
-Lipschitz. We apply Lemma 2·7 with
![]() $\varepsilon = (M \tau^{-1})^{-O(d^{O(1)})}$
sufficiently small and replace each of the possible
$\varepsilon = (M \tau^{-1})^{-O(d^{O(1)})}$
sufficiently small and replace each of the possible
![]() $d_1\cdot (d_2-d_1)$
possible combinations for the “smoothed parts” simultaneously in each term. We find that
$d_1\cdot (d_2-d_1)$
possible combinations for the “smoothed parts” simultaneously in each term. We find that
 \begin{align}&\sup_{x\in G}\bigg|F_i(x\Gamma) \nonumber\\[5pt] &- \sum_{k\in I}c_k e\bigg(\sum_{j=1}^{d}T_{k,j}x_j + \widetilde{\varphi}_k(x_{\le d_1},\lfloor x_{\le d_1}\rfloor_i) + \widetilde{\phi}_k(x_{\le d_2},\lfloor x_{\le d_1}\rfloor_i)+\widetilde{\sigma}_k(x_{\le d_2},x_{\le d_1})\bigg) \bigg|\le 2\tau\end{align}
\begin{align}&\sup_{x\in G}\bigg|F_i(x\Gamma) \nonumber\\[5pt] &- \sum_{k\in I}c_k e\bigg(\sum_{j=1}^{d}T_{k,j}x_j + \widetilde{\varphi}_k(x_{\le d_1},\lfloor x_{\le d_1}\rfloor_i) + \widetilde{\phi}_k(x_{\le d_2},\lfloor x_{\le d_1}\rfloor_i)+\widetilde{\sigma}_k(x_{\le d_2},x_{\le d_1})\bigg) \bigg|\le 2\tau\end{align}
with
![]() $|I|\le (M \tau^{-1})^{O(d^{O(1)})}$
,
$|I|\le (M \tau^{-1})^{O(d^{O(1)})}$
,
![]() $|c_k|\le (M\tau^{-1})^{O(d^{O(1)})}$
,
$|c_k|\le (M\tau^{-1})^{O(d^{O(1)})}$
,
![]() $\widetilde{\varphi}_k$
is an at most degree 3 polynomial,
$\widetilde{\varphi}_k$
is an at most degree 3 polynomial,
![]() $\widetilde{\phi}_k$
and
$\widetilde{\phi}_k$
and
![]() $\widetilde{\sigma}_k$
are bilinear forms, and all coefficients of these forms bounded by
$\widetilde{\sigma}_k$
are bilinear forms, and all coefficients of these forms bounded by
![]() $(M \tau^{-1})^{O(d^{O(1)})}$
. Explicitly, we used Lemma 2·7 on
$(M \tau^{-1})^{O(d^{O(1)})}$
. Explicitly, we used Lemma 2·7 on
![]() $(\mathbb{R}/\mathbb{Z})^2$
with parameter
$(\mathbb{R}/\mathbb{Z})^2$
with parameter
![]() $\varepsilon$
many times and multiplied the representations together.
$\varepsilon$
many times and multiplied the representations together.
We now specialise to the case of interest. Note that our primary concern is with the case where
![]() $x = g(n)$
and therefore
$x = g(n)$
and therefore
![]() $x_j = p_j(n)$
where
$x_j = p_j(n)$
where
![]() $\deg p_j\le i$
for
$\deg p_j\le i$
for
![]() $j\le d_i$
if
$j\le d_i$
if
![]() $i\in\{1,2,3\}$
. Using the representation (2·7) and collecting terms we have
$i\in\{1,2,3\}$
. Using the representation (2·7) and collecting terms we have
where
![]() $H_k\colon\mathbb{Z}\to\mathbb{R}$
is a sum of terms of the form:
$H_k\colon\mathbb{Z}\to\mathbb{R}$
is a sum of terms of the form:
-
(i)
 $\alpha n^3 + \beta n^2 + \gamma n$
;
$\alpha n^3 + \beta n^2 + \gamma n$
; -
(ii)
 $(\alpha n^2 + \beta n + \gamma) \lfloor p_j(n)\rfloor_{i,j}$
for
$(\alpha n^2 + \beta n + \gamma) \lfloor p_j(n)\rfloor_{i,j}$
for
 $1\le j\le d_1$
;
$1\le j\le d_1$
; -
(iii)
 $(\alpha n + \beta)\lfloor p_j(n)\rfloor_{i,j}\lfloor p_k(n)\rfloor_{i,k}$
for
$(\alpha n + \beta)\lfloor p_j(n)\rfloor_{i,j}\lfloor p_k(n)\rfloor_{i,k}$
for
 $1\le j\le k\le d_1$
;
$1\le j\le k\le d_1$
; -
(vi)
 $\gamma\lfloor p_j(n)\rfloor_{i,j}\lfloor p_k(n)\rfloor_{i,k}\lfloor p_\ell(n)\rfloor_{i,\ell}$
for
$\gamma\lfloor p_j(n)\rfloor_{i,j}\lfloor p_k(n)\rfloor_{i,k}\lfloor p_\ell(n)\rfloor_{i,\ell}$
for
 $1\le j\le k\le \ell \le d_1$
;
$1\le j\le k\le \ell \le d_1$
;
note that one can always collect terms so that there are at most
![]() $d^{O(1)}$
terms in each expression.
$d^{O(1)}$
terms in each expression.
Step 4. N-periodicity and introducing Bohr sets. Let
![]() $\rho=1/100$
, which will be the radius of our Bohr sets. Now, note that the expressions
$\rho=1/100$
, which will be the radius of our Bohr sets. Now, note that the expressions
![]() $e(H_k(n))$
are not “obviously” N-periodic. We will artificially make them so via a partition of unity argument. There exist smooth
$e(H_k(n))$
are not “obviously” N-periodic. We will artificially make them so via a partition of unity argument. There exist smooth
![]() $\chi_1,\ldots,\chi_{10^{3}}$
such that
$\chi_1,\ldots,\chi_{10^{3}}$
such that
![]() $\chi_j\colon(\mathbb{R}/\mathbb{Z})\to \mathbb{R}$
are nonnegative with
$\chi_j\colon(\mathbb{R}/\mathbb{Z})\to \mathbb{R}$
are nonnegative with
![]() $\operatorname{supp}(\chi_{j})\subseteq[j/10^{3}, (j+2)/10^{3}) \;\mathrm{mod}\;1$
and
$\operatorname{supp}(\chi_{j})\subseteq[j/10^{3}, (j+2)/10^{3}) \;\mathrm{mod}\;1$
and
![]() $\sum_{j=1}^{10^{3}}\chi_j = 1$
. We have
$\sum_{j=1}^{10^{3}}\chi_j = 1$
. We have
 \begin{align*}&F_i(g(n)\Gamma) = \sum_{j\in [10^{3}]}\chi_j(n/N)F_i(g(n)\Gamma),\\\sup_{\substack{n\in \mathbb{Z}\\ j\in [10^{3}]}}\bigg|&F_i(g(n)\Gamma)\chi_j(n/N) - \chi_j(n/N)\sum_{k\in I}c_k e(H_k(n)) \bigg|\le O(\tau).\end{align*}
\begin{align*}&F_i(g(n)\Gamma) = \sum_{j\in [10^{3}]}\chi_j(n/N)F_i(g(n)\Gamma),\\\sup_{\substack{n\in \mathbb{Z}\\ j\in [10^{3}]}}\bigg|&F_i(g(n)\Gamma)\chi_j(n/N) - \chi_j(n/N)\sum_{k\in I}c_k e(H_k(n)) \bigg|\le O(\tau).\end{align*}
Now fix
![]() $j\in [10^{3}]$
; such a term only contributes when
$j\in [10^{3}]$
; such a term only contributes when
![]() $n/N \in [j/10^{3}, (j+2)/10^{3}) \mod 1$
. Next note that each
$n/N \in [j/10^{3}, (j+2)/10^{3}) \mod 1$
. Next note that each
![]() $p_\ell(n) = \alpha_\ell n$
for
$p_\ell(n) = \alpha_\ell n$
for
![]() $\ell\le d_1$
and because the initial nilsequence
$\ell\le d_1$
and because the initial nilsequence
![]() $g(n)\Gamma$
is N-periodic, by [
Reference Leng23
, lemma A·12] we have that
$g(n)\Gamma$
is N-periodic, by [
Reference Leng23
, lemma A·12] we have that
![]() $\alpha_\ell \in (1/N)\mathbb{Z}$
.
$\alpha_\ell \in (1/N)\mathbb{Z}$
.
Note that in order for
![]() $\chi_j(n/N)F_i(g(n)\Gamma)$
to be nonzero, we need that:
$\chi_j(n/N)F_i(g(n)\Gamma)$
to be nonzero, we need that:
-
(i)
 $n/N \equiv [j/10^{3}, (j+2)/10^{3}) \mod 1$
;
$n/N \equiv [j/10^{3}, (j+2)/10^{3}) \mod 1$
; -
(ii)
 $\{p_\ell(n)\}_{i,\ell} \in [\beta_\ell^{(i)}-10^{-3},\beta_\ell^{(i)}+10^{-3})$
for all
$\{p_\ell(n)\}_{i,\ell} \in [\beta_\ell^{(i)}-10^{-3},\beta_\ell^{(i)}+10^{-3})$
for all
 $\ell\in[d_1]$
.
$\ell\in[d_1]$
.
These conditions are clearly N-periodic and in fact all such n lie in a shifted Bohr set with frequency set
![]() $S = \{1/N\} \cup \{\alpha_\ell\}_{1\le \ell\le d_1}\subseteq(1/N)\mathbb{Z}$
. If the corresponding shifted Bohr set is empty we know that
$S = \{1/N\} \cup \{\alpha_\ell\}_{1\le \ell\le d_1}\subseteq(1/N)\mathbb{Z}$
. If the corresponding shifted Bohr set is empty we know that
![]() $\chi_j(n/N)F_i(g(n)\Gamma) = 0$
and we approximate
$\chi_j(n/N)F_i(g(n)\Gamma) = 0$
and we approximate
![]() $\chi_j(n/N)F_i(g(n)\Gamma)$
by 0. Else there is
$\chi_j(n/N)F_i(g(n)\Gamma)$
by 0. Else there is
![]() $y_j\in\mathbb{Z}/N\mathbb{Z}$
such that
$y_j\in\mathbb{Z}/N\mathbb{Z}$
such that
![]() $y_j/N \equiv [j/10^{3}, (j+2)/10^{3}) \mod 1$
and
$y_j/N \equiv [j/10^{3}, (j+2)/10^{3}) \mod 1$
and
![]() $\{\alpha_\ell y_j\}_{i,\ell} \in [\beta_\ell^{(i)}-10^{-3},\beta_\ell^{(i)}+10^{-3})$
for
$\{\alpha_\ell y_j\}_{i,\ell} \in [\beta_\ell^{(i)}-10^{-3},\beta_\ell^{(i)}+10^{-3})$
for
![]() $\ell\in[d_1]$
. Letting
$\ell\in[d_1]$
. Letting
![]() $J_i$
be the set of j for which this shifted Bohr set is nonempty, we have
$J_i$
be the set of j for which this shifted Bohr set is nonempty, we have
 \[\sup_{\substack{n\in \mathbb{Z}\\ j\in J_i}}\bigg|F_i(g(n)\Gamma)\chi_j(n/N) - \mathbb{1}_{n\in y_j + B(S, \rho)}\chi_j(n/N)\sum_{k\in I}c_k e(H_k(n)) \bigg|\le O(\tau).\]
\[\sup_{\substack{n\in \mathbb{Z}\\ j\in J_i}}\bigg|F_i(g(n)\Gamma)\chi_j(n/N) - \mathbb{1}_{n\in y_j + B(S, \rho)}\chi_j(n/N)\sum_{k\in I}c_k e(H_k(n)) \bigg|\le O(\tau).\]
We now apply Fourier expansion on
![]() $\chi_j$
using Lemma 2·7 on the torus
$\chi_j$
using Lemma 2·7 on the torus
![]() $\mathbb{R}/\mathbb{Z}$
and appropriately chosen error parameter
$\mathbb{R}/\mathbb{Z}$
and appropriately chosen error parameter
![]() $\tau' = (M\tau^{-1})^{-O(d^{O(1)})}$
. We find
$\tau' = (M\tau^{-1})^{-O(d^{O(1)})}$
. We find
 \begin{equation}\sup_{\substack{n\in\mathbb{Z}\\j\in J_i}}\bigg|F_i(g(n)\Gamma)\chi_j(n/N) - \mathbb{1}_{n\in y_j + B(S,\rho)}\chi_j(n/N)\sum_{k\in I, |\xi|\le (\tau')^{-O(1)}}c_kd_{\xi} e(H_k(n) + \xi n/N) \bigg|\le O(\tau)\end{equation}
\begin{equation}\sup_{\substack{n\in\mathbb{Z}\\j\in J_i}}\bigg|F_i(g(n)\Gamma)\chi_j(n/N) - \mathbb{1}_{n\in y_j + B(S,\rho)}\chi_j(n/N)\sum_{k\in I, |\xi|\le (\tau')^{-O(1)}}c_kd_{\xi} e(H_k(n) + \xi n/N) \bigg|\le O(\tau)\end{equation}
with
![]() $|d_{\xi}|\le (\tau')^{-O(1)}$
.
$|d_{\xi}|\le (\tau')^{-O(1)}$
.
Given
![]() $n\in y_j + B(S,\rho)$
, we will now replace
$n\in y_j + B(S,\rho)$
, we will now replace
![]() $H_k(n)$
by
$H_k(n)$
by
![]() $H_{k,j}(n)$
so that the latter is N-periodic (and it will be locally cubic on
$H_{k,j}(n)$
so that the latter is N-periodic (and it will be locally cubic on
![]() $y_j+B(S,\rho)$
). We fix an interval
$y_j+B(S,\rho)$
). We fix an interval
![]() $I_j \in [\!-\!N,N)$
of integers of length at most
$I_j \in [\!-\!N,N)$
of integers of length at most
![]() $\lceil N/50\rceil$
such that for each
$\lceil N/50\rceil$
such that for each
![]() $n\in y_j + B(S,\rho)$
there is a unique integer
$n\in y_j + B(S,\rho)$
there is a unique integer
![]() $n'\in I_j$
such that
$n'\in I_j$
such that
![]() $n'\equiv n \;\mathrm{mod}\;N$
. This exists since
$n'\equiv n \;\mathrm{mod}\;N$
. This exists since
![]() $1/N\in S$
. We then define
$1/N\in S$
. We then define
![]() $H_{k,j}(n) \equiv H_k(n') \mod 1$
for such
$H_{k,j}(n) \equiv H_k(n') \mod 1$
for such
![]() $n\in y_j + B(S,\rho)$
and
$n\in y_j + B(S,\rho)$
and
![]() $H_{k,j}(n) = 0$
otherwise; note that
$H_{k,j}(n) = 0$
otherwise; note that
![]() $H_{k,j}(n)$
is taking values in
$H_{k,j}(n)$
is taking values in
![]() $\mathbb{R}/\mathbb{Z}$
which is sufficient as we are plugging these values into the exponential function.
$\mathbb{R}/\mathbb{Z}$
which is sufficient as we are plugging these values into the exponential function.
It is easy to see that (2·8) holds with
![]() $H_k(n)+\xi\cdot n/N$
replaced by
$H_k(n)+\xi\cdot n/N$
replaced by
![]() $H_{k,j}(n)$
since everything in the inequality except for potentially
$H_{k,j}(n)$
since everything in the inequality except for potentially
![]() $H_k(n)$
is N-periodic (recall
$H_k(n)$
is N-periodic (recall
![]() $S\subseteq(1/N)\mathbb{Z}$
), and there is a supremum over
$S\subseteq(1/N)\mathbb{Z}$
), and there is a supremum over
![]() $n\in\mathbb{Z}$
on the outside. So, we have
$n\in\mathbb{Z}$
on the outside. So, we have
 \[\sup_{\substack{n\in \mathbb{Z}\\ j\in J_i}}\bigg|F_i(g(n)\Gamma)\chi_j(n/N) - \mathbb{1}_{n\in y_j + B(S, \rho)}\sum_{k\in I, |\xi|\le (\tau')^{-O(1)}}c_k d_{\xi} e(H_{k,j}(n)+\xi n/N) \bigg|\le O(\tau),\]
\[\sup_{\substack{n\in \mathbb{Z}\\ j\in J_i}}\bigg|F_i(g(n)\Gamma)\chi_j(n/N) - \mathbb{1}_{n\in y_j + B(S, \rho)}\sum_{k\in I, |\xi|\le (\tau')^{-O(1)}}c_k d_{\xi} e(H_{k,j}(n)+\xi n/N) \bigg|\le O(\tau),\]
where
![]() $H_{k,j}(n)$
is N-periodic by construction. Taking
$H_{k,j}(n)$
is N-periodic by construction. Taking
![]() $\tau = \eta M^{-O(d^{O(1)})}$
and summing over j and i then finishes the proof modulo showing that
$\tau = \eta M^{-O(d^{O(1)})}$
and summing over j and i then finishes the proof modulo showing that
![]() $H_{k,j}(n)$
is a locally cubic function on
$H_{k,j}(n)$
is a locally cubic function on
![]() $y_j + B(S,\rho)$
.
$y_j + B(S,\rho)$
.
Step 5. Local cubicity on shifted Bohr sets. Fix i,
![]() $j\in J_i$
, and
$j\in J_i$
, and
![]() $k\in I$
. We wish to show local cubicity of
$k\in I$
. We wish to show local cubicity of
![]() $H_{k,j}$
on
$H_{k,j}$
on
![]() $y_j+B(S,\rho)$
. Suppose that
$y_j+B(S,\rho)$
. Suppose that
![]() $n,h_1,h_2,h_3\in\mathbb{Z}/N\mathbb{Z}$
are such that
$n,h_1,h_2,h_3\in\mathbb{Z}/N\mathbb{Z}$
are such that
![]() $n + \sum_{\ell=1}^{3}\epsilon_\ell h_\ell\in y_j + B(S,\rho)$
for all
$n + \sum_{\ell=1}^{3}\epsilon_\ell h_\ell\in y_j + B(S,\rho)$
for all
![]() $(\epsilon_1,\epsilon_2,\epsilon_3)\in \{0,1\}^3$
. We consider the representatives of
$(\epsilon_1,\epsilon_2,\epsilon_3)\in \{0,1\}^3$
. We consider the representatives of
![]() $n + \sum_{\ell=1}^{3}\epsilon_\ell h_\ell$
in
$n + \sum_{\ell=1}^{3}\epsilon_\ell h_\ell$
in
![]() $I_j$
; we see that there exist
$I_j$
; we see that there exist
![]() $n',h_1',h_2',h_3'\in \mathbb{Z}$
such that
$n',h_1',h_2',h_3'\in \mathbb{Z}$
such that
![]() $n' + \sum_{\ell=1}^{3}\epsilon_\ell h_\ell' \equiv n + \sum_{\ell=1}^{3}\epsilon_\ell h_\ell \;\mathrm{mod}\;N$
and
$n' + \sum_{\ell=1}^{3}\epsilon_\ell h_\ell' \equiv n + \sum_{\ell=1}^{3}\epsilon_\ell h_\ell \;\mathrm{mod}\;N$
and
![]() $n' + \sum_{\ell=1}^{3}\epsilon_\ell h_\ell'\in I_j$
for all
$n' + \sum_{\ell=1}^{3}\epsilon_\ell h_\ell'\in I_j$
for all
![]() $\epsilon\in\{0,1\}^3$
. Indeed, one can look at the representatives of each
$\epsilon\in\{0,1\}^3$
. Indeed, one can look at the representatives of each
![]() $n + \sum_{\ell=1}^{3}\epsilon_\ell h_\ell$
in
$n + \sum_{\ell=1}^{3}\epsilon_\ell h_\ell$
in
![]() $I_j$
, and use the fact that if
$I_j$
, and use the fact that if
![]() $t_1 + t_2 \equiv t_3 + t_4 \;\mathrm{mod}\;N$
with
$t_1 + t_2 \equiv t_3 + t_4 \;\mathrm{mod}\;N$
with
![]() $t_i\in I_j$
then
$t_i\in I_j$
then
![]() $t_1 + t_2 = t_3 + t_4$
(since
$t_1 + t_2 = t_3 + t_4$
(since
![]() $I_j$
has length at most
$I_j$
has length at most
![]() $\lceil N/50\rceil$
).
$\lceil N/50\rceil$
).
Therefore it suffices to prove that
![]() $H_k\colon\mathbb{Z}\to\mathbb{R}$
is locally cubic on
$H_k\colon\mathbb{Z}\to\mathbb{R}$
is locally cubic on
![]() $y_j+B(S,\rho)$
. Recalling the classification of
$y_j+B(S,\rho)$
. Recalling the classification of
![]() $H_k(n)$
as a sum of terms of various kinds, it suffices to verify this for each individual function type which is combined to give
$H_k(n)$
as a sum of terms of various kinds, it suffices to verify this for each individual function type which is combined to give
![]() $H_k(n)$
.
$H_k(n)$
.
Note that pure polynomials are always the correct degree (on all of
![]() $\mathbb{Z}$
). By Lemma 2·8 it suffices to verify that
$\mathbb{Z}$
). By Lemma 2·8 it suffices to verify that
![]() $\lfloor \alpha_\ell n \rfloor_{i,\ell}$
is locally linear on
$\lfloor \alpha_\ell n \rfloor_{i,\ell}$
is locally linear on
![]() $y_j+B(S,\rho)$
for
$y_j+B(S,\rho)$
for
![]() $1\le\ell\le d_1$
.
$1\le\ell\le d_1$
.
Given
![]() $n,n + h_1, n+h_2, n+h_1+h_2\in y_j + B(S,\rho)$
we have that
$n,n + h_1, n+h_2, n+h_1+h_2\in y_j + B(S,\rho)$
we have that
 \begin{align*}&\lfloor \alpha_\ell n \rfloor_{i,\ell} - \lfloor \alpha_\ell (n+h_1) \rfloor_{i,\ell} - \lfloor \alpha_\ell (n+h_2) \rfloor_{i,\ell} + \lfloor \alpha_\ell (n+h_1+h_2) \rfloor_{i,\ell} \in \mathbb{Z},\\&\big|\lfloor \alpha_\ell n \rfloor_{i,\ell} - \lfloor \alpha_\ell (n+h_1) \rfloor_{i,\ell} - \lfloor \alpha_\ell (n+h_2) \rfloor_{i,\ell} + \lfloor \alpha_\ell (n+h_1+h_2) \rfloor_{i,\ell} \big|\\&= \big|\{ \alpha_\ell n \}_{i,\ell} - \{ \alpha_\ell (n+h_1) \}_{i,\ell} - \{ \alpha_\ell (n+h_2) \}_{i,\ell} + \{ \alpha_\ell (n+h_1+h_2) \}_{i,\ell} \big|\le 1/2,\end{align*}
\begin{align*}&\lfloor \alpha_\ell n \rfloor_{i,\ell} - \lfloor \alpha_\ell (n+h_1) \rfloor_{i,\ell} - \lfloor \alpha_\ell (n+h_2) \rfloor_{i,\ell} + \lfloor \alpha_\ell (n+h_1+h_2) \rfloor_{i,\ell} \in \mathbb{Z},\\&\big|\lfloor \alpha_\ell n \rfloor_{i,\ell} - \lfloor \alpha_\ell (n+h_1) \rfloor_{i,\ell} - \lfloor \alpha_\ell (n+h_2) \rfloor_{i,\ell} + \lfloor \alpha_\ell (n+h_1+h_2) \rfloor_{i,\ell} \big|\\&= \big|\{ \alpha_\ell n \}_{i,\ell} - \{ \alpha_\ell (n+h_1) \}_{i,\ell} - \{ \alpha_\ell (n+h_2) \}_{i,\ell} + \{ \alpha_\ell (n+h_1+h_2) \}_{i,\ell} \big|\le 1/2,\end{align*}
the inequality using that
![]() $\rho=1/100$
and every
$\rho=1/100$
and every
![]() $\alpha_\ell(n+\epsilon_1h_1+\epsilon_2h_2)$
must be close in
$\alpha_\ell(n+\epsilon_1h_1+\epsilon_2h_2)$
must be close in
![]() $\mathbb{R}/\mathbb{Z}$
to
$\mathbb{R}/\mathbb{Z}$
to
![]() $\alpha_\ell y_j$
. Additionally, we recall
$\alpha_\ell y_j$
. Additionally, we recall
![]() $\{\alpha_\ell y_j\}\in[\beta_\ell^{(i)}-10^{-3},\beta_\ell^{(i)}+10^{-3})$
which implies that there is no discontinuity in
$\{\alpha_\ell y_j\}\in[\beta_\ell^{(i)}-10^{-3},\beta_\ell^{(i)}+10^{-3})$
which implies that there is no discontinuity in
![]() $\{\cdot\}_{i,\ell}$
in the area of consideration.
$\{\cdot\}_{i,\ell}$
in the area of consideration.
Therefore
for
![]() $n,n + h_1, n+h_2, n+h_1+h_2\in y_j + B(S,\rho)$
as desired. This (finally) completes the proof.
$n,n + h_1, n+h_2, n+h_1+h_2\in y_j + B(S,\rho)$
as desired. This (finally) completes the proof.
3. Proof of Theorem 1·1 given Proposition 1·4
In this section, we convert Proposition 1·4 into a density increment using the strategy of Heath-Brown [ Reference Heath-Brown16 ] and Szemerédi [ Reference Szemerédi35 ]. Our treatment is closely modeled on that of Green and Tao [ Reference Green and Tao13 ]; the crucial idea is that one may group together a large number of phases before passing to a subprogression.
Throughout this section we will consider functions
![]() $f\colon[N']\to[\!-\!1,1]$
corresponding to sets and shifted indicators. By Bertrand’s postulate, we may find a prime N such that
$f\colon[N']\to[\!-\!1,1]$
corresponding to sets and shifted indicators. By Bertrand’s postulate, we may find a prime N such that
![]() $1024 N' \le N \le 2048 N'$
. We may thus embed [N
′] inside
$1024 N' \le N \le 2048 N'$
. We may thus embed [N
′] inside
![]() $\mathbb{Z}/(N\mathbb{Z})$
and lift f to
$\mathbb{Z}/(N\mathbb{Z})$
and lift f to
![]() $\mathbb{Z}/N\mathbb{Z}$
(mapping inputs not congruent to an element of [N
′] to 0). We define the quintilinear operator
$\mathbb{Z}/N\mathbb{Z}$
(mapping inputs not congruent to an element of [N
′] to 0). We define the quintilinear operator
 \[\Lambda(f_1,\ldots,f_5) = \mathbb{E}_{x,y\in\mathbb{Z}/N\mathbb{Z}} \prod_{k=1}^{5}f_k(x+(k-1)y)\text{ and }\Lambda(f) = \Lambda(f,f,f,f,f).\]
\[\Lambda(f_1,\ldots,f_5) = \mathbb{E}_{x,y\in\mathbb{Z}/N\mathbb{Z}} \prod_{k=1}^{5}f_k(x+(k-1)y)\text{ and }\Lambda(f) = \Lambda(f,f,f,f,f).\]
We now state the key claim for this section, which we will prove in Section 3.3
Proposition 3·1. Fix a constant
![]() $c \gt 0$
. There exist
$c \gt 0$
. There exist
![]() $c' \gt 0$
and
$c' \gt 0$
and
![]() $C \gt 0$
such that the following holds. Consider a function
$C \gt 0$
such that the following holds. Consider a function
![]() $f\colon[N']\to [0,1]$
such that
$f\colon[N']\to [0,1]$
such that
![]() $\mathbb{E}_{n\in [N']}f(n) = \delta \gt 0$
and a prime N such that
$\mathbb{E}_{n\in [N']}f(n) = \delta \gt 0$
and a prime N such that
![]() $1024 N'\le N\le 2048 N'$
. Let
$1024 N'\le N\le 2048 N'$
. Let
![]() $M(\delta) = \exp\!((\!\log\!(1/\delta))^C)$
. At least one of the following possibilities always holds:
$M(\delta) = \exp\!((\!\log\!(1/\delta))^C)$
. At least one of the following possibilities always holds:
-
(i)
 $N'\le\exp\!(M(\delta))$
;
$N'\le\exp\!(M(\delta))$
; -
(ii)
 $\big|\Lambda(f) - \Lambda(\delta \mathbb{1}_{[N']})\big| \le c \delta^{5}$
;
$\big|\Lambda(f) - \Lambda(\delta \mathbb{1}_{[N']})\big| \le c \delta^{5}$
; -
(iii) there exists an arithmetic progression P of length at least
 $N^{1/M(\delta)}$
such that
$N^{1/M(\delta)}$
such that  \[\mathbb{E}_{n\in P}f(n)\ge (1+c')\delta.\]
\[\mathbb{E}_{n\in P}f(n)\ge (1+c')\delta.\]
With this, we can prove the main result.
Proof of Theorem 1·1 given Proposition 3·1. Suppose that
![]() $A\subseteq [N]$
has size
$A\subseteq [N]$
has size
![]() $\delta N$
and has no 5-term arithmetic progressions. We now perform the density increment strategy using
$\delta N$
and has no 5-term arithmetic progressions. We now perform the density increment strategy using
![]() $A_0 = A$
,
$A_0 = A$
,
![]() $N_0' = N$
, and
$N_0' = N$
, and
![]() $\delta_0 = \delta$
.
$\delta_0 = \delta$
.
For each
![]() $N_i'$
choose a prime
$N_i'$
choose a prime
![]() $N_i$
between
$N_i$
between
![]() $1024 N_i'\le N_i\le 2048 N_i'$
. If
$1024 N_i'\le N_i\le 2048 N_i'$
. If
![]() $N_i'\le M(\delta_i)$
, we immediately terminate. Else note that
$N_i'\le M(\delta_i)$
, we immediately terminate. Else note that
as
![]() $A_i$
is free of 5-term arithmetic progressions. Therefore the third case in the trichotomy must hold and there exists a long progression
$A_i$
is free of 5-term arithmetic progressions. Therefore the third case in the trichotomy must hold and there exists a long progression
![]() $P_i$
on which the density of
$P_i$
on which the density of
![]() $A_i$
increases by a factor of at least
$A_i$
increases by a factor of at least
![]() $(1+c')$
. Let
$(1+c')$
. Let
![]() $A_{i+1}$
be
$A_{i+1}$
be
![]() $A_i\cap P_i$
rescaled so that
$A_i\cap P_i$
rescaled so that
![]() $P_i$
starts at 0 and has common difference 1, let
$P_i$
starts at 0 and has common difference 1, let
![]() $N_{i+1}' = |P_i|$
, and let
$N_{i+1}' = |P_i|$
, and let
![]() $\delta_{i+1} = |A_i\cap P_i|/|P_i|\ge(1+c')\delta_i$
.
$\delta_{i+1} = |A_i\cap P_i|/|P_i|\ge(1+c')\delta_i$
.
Since the density of a set cannot exceed 1, we must terminate in at most
![]() $O(\!\log\!(1/\delta))$
iterations. If we terminate at i, we must have
$O(\!\log\!(1/\delta))$
iterations. If we terminate at i, we must have
Rearranging this gives exactly that
or, as desired,
3·1. Inverse theorem relative to linear and cubic factors
We introduce a framework for studying functions satisfying a correlation as given by Proposition 1·4, considering a
![]() $\sigma$
-algebra (or factor) which incorporates the information of the approximate value of our linear and cubic functions on [N]. Our treatment closely follows that of Green and Tao [
Reference Green and Tao13
] (and uses elements from Peluse and Prendiville [
Reference Peluse and Prendiville25
]).
$\sigma$
-algebra (or factor) which incorporates the information of the approximate value of our linear and cubic functions on [N]. Our treatment closely follows that of Green and Tao [
Reference Green and Tao13
] (and uses elements from Peluse and Prendiville [
Reference Peluse and Prendiville25
]).
Definition 3·2. We define a factor
![]() $\mathcal{B}$
of
$\mathcal{B}$
of
![]() $\mathbb{Z}/N\mathbb{Z}$
to be a partition
$\mathbb{Z}/N\mathbb{Z}$
to be a partition
![]() $\mathbb{Z}/N\mathbb{Z} = \bigsqcup_{B\in \mathcal{B}}B$
. We define
$\mathbb{Z}/N\mathbb{Z} = \bigsqcup_{B\in \mathcal{B}}B$
. We define
![]() $\mathcal{B}(x)$
for
$\mathcal{B}(x)$
for
![]() $x\in\mathbb{Z}/N\mathbb{Z}$
to be the part of
$x\in\mathbb{Z}/N\mathbb{Z}$
to be the part of
![]() $\mathcal{B}$
that contains x.
$\mathcal{B}$
that contains x.
We say
![]() $\mathcal{B}'$
refines
$\mathcal{B}'$
refines
![]() $\mathcal{B}$
if every part of
$\mathcal{B}$
if every part of
![]() $\mathcal{B}$
can be written as a disjoint union of parts of
$\mathcal{B}$
can be written as a disjoint union of parts of
![]() $\mathcal{B}'$
. We define a join of a sequence of factors to be the partition (discarding empty parts)
$\mathcal{B}'$
. We define a join of a sequence of factors to be the partition (discarding empty parts)
Define a function
![]() $\phi\colon S\to\mathbb{R}/\mathbb{Z}$
for
$\phi\colon S\to\mathbb{R}/\mathbb{Z}$
for
![]() $S\subseteq\mathbb{Z}/N\mathbb{Z}$
to be irrational if
$S\subseteq\mathbb{Z}/N\mathbb{Z}$
to be irrational if
![]() $\phi$
takes on irrational values. Define the factor
$\phi$
takes on irrational values. Define the factor
![]() $\mathcal{B}_{\phi,K}$
with respect to
$\mathcal{B}_{\phi,K}$
with respect to
![]() $\phi$
of resolution K as the partition
$\phi$
of resolution K as the partition
(Since
![]() $\phi$
is irrational this is indeed a disjoint partition.) We further say that
$\phi$
is irrational this is indeed a disjoint partition.) We further say that
![]() $\phi$
respects a factor
$\phi$
respects a factor
![]() $\mathcal{B}$
if
$\mathcal{B}$
if
![]() $\mathcal{B}$
refines
$\mathcal{B}$
refines
![]() $S\sqcup ((\mathbb{Z}/N\mathbb{Z})\setminus S)$
.
$S\sqcup ((\mathbb{Z}/N\mathbb{Z})\setminus S)$
.
We define a factor of complexity
![]() $(d_1,d_2)$
and resolution K via the data of irrational linear functions
$(d_1,d_2)$
and resolution K via the data of irrational linear functions
![]() $\phi_1,\ldots,\phi_{d_1}$
(defined on
$\phi_1,\ldots,\phi_{d_1}$
(defined on
![]() $\mathbb{Z}/N\mathbb{Z}$
) and irrational locally cubic functions
$\mathbb{Z}/N\mathbb{Z}$
) and irrational locally cubic functions
![]() $\phi_1',\ldots,\phi_{d_2}'$
(defined on subsets of
$\phi_1',\ldots,\phi_{d_2}'$
(defined on subsets of
![]() $\mathbb{Z}/N\mathbb{Z}$
) which respect
$\mathbb{Z}/N\mathbb{Z}$
) which respect
![]() $\bigvee_{1\le j\le d_1}\mathcal{B}_{\phi_j,K}$
. The associated factor is
$\bigvee_{1\le j\le d_1}\mathcal{B}_{\phi_j,K}$
. The associated factor is
![]() $\bigvee_{1\le j\le d_1}\mathcal{B}_{\phi_j,K} \vee \bigvee_{1\le j\le d_1}\mathcal{B}_{\phi_j',K}$
.
$\bigvee_{1\le j\le d_1}\mathcal{B}_{\phi_j,K} \vee \bigvee_{1\le j\le d_1}\mathcal{B}_{\phi_j',K}$
.
Finally, given a factor
![]() $\mathcal{B}$
we define
$\mathcal{B}$
we define
![]() $\Pi_{\mathcal{B}}f$
by
$\Pi_{\mathcal{B}}f$
by
Remark. We ensure all functions
![]() $\phi$
we consider are irrational in order to avoid issues regarding the hitting exactly the boundary of the factor. Note that if a locally cubic function
$\phi$
we consider are irrational in order to avoid issues regarding the hitting exactly the boundary of the factor. Note that if a locally cubic function
![]() $\phi$
respects a partition
$\phi$
respects a partition
![]() $\mathcal{B}$
then we see that the support set is in the
$\mathcal{B}$
then we see that the support set is in the
![]() $\sigma$
-algebra generated by
$\sigma$
-algebra generated by
![]() $\mathcal{B}$
. In particular, we can treat
$\mathcal{B}$
. In particular, we can treat
![]() $\phi$
as either “undefined” on an atom
$\phi$
as either “undefined” on an atom
![]() $\mathcal{B}$
or as locally cubic on the associated atom.
$\mathcal{B}$
or as locally cubic on the associated atom.
We now restate Proposition 1·4 in the language of factors.
Lemma 3·3. There exists
![]() $C \gt 0$
such that the following holds. Fix
$C \gt 0$
such that the following holds. Fix
![]() $\eta \gt 0$
and let f be a function
$\eta \gt 0$
and let f be a function
![]() $f\colon\mathbb{Z}/N\mathbb{Z}\to[0,1]$
such that
$f\colon\mathbb{Z}/N\mathbb{Z}\to[0,1]$
such that
![]() $\lVert f\rVert_{U^4(\mathbb{Z}/N\mathbb{Z})}\ge\eta$
.
$\lVert f\rVert_{U^4(\mathbb{Z}/N\mathbb{Z})}\ge\eta$
.
Let
![]() $M(\eta) = \exp\!((\!\log\!(1/\eta))^C)$
and fix an integer
$M(\eta) = \exp\!((\!\log\!(1/\eta))^C)$
and fix an integer
![]() $K\ge \exp\!(M(\eta))$
. Suppose that
$K\ge \exp\!(M(\eta))$
. Suppose that
![]() $N\ge 8K$
. There exist
$N\ge 8K$
. There exist
![]() $d\le M(\eta)$
and a factor
$d\le M(\eta)$
and a factor
![]() $\mathcal{B}$
of complexity (d,1) and resolution K such that
$\mathcal{B}$
of complexity (d,1) and resolution K such that
Proof. By Proposition 1·4, there exist
![]() $\rho=1/100$
,
$\rho=1/100$
,
![]() $S\subseteq (1/N)\mathbb{Z}$
with
$S\subseteq (1/N)\mathbb{Z}$
with
![]() $|S|\ll(\!\log\!(1/\eta))^{C}$
(say
$|S|\ll(\!\log\!(1/\eta))^{C}$
(say
![]() $|S|=d$
), and
$|S|=d$
), and
![]() $y\in \mathbb{Z}/N\mathbb{Z}$
such that
$y\in \mathbb{Z}/N\mathbb{Z}$
such that
![]() $B=B(S,\rho)$
is a Bohr set and
$B=B(S,\rho)$
is a Bohr set and
![]() $\phi\colon y+B\to\mathbb{R}/\mathbb{Z}$
is a locally cubic phase function such that
$\phi\colon y+B\to\mathbb{R}/\mathbb{Z}$
is a locally cubic phase function such that
Let C
′ be a sufficiently large constant and assume
![]() $K \ge \exp\!((\!\log\!(1/\eta))^{C'})$
. Take
$K \ge \exp\!((\!\log\!(1/\eta))^{C'})$
. Take
![]() $\phi_i\colon\mathbb{Z}/N\mathbb{Z}\to \mathbb{R}/\mathbb{Z}$
to be
$\phi_i\colon\mathbb{Z}/N\mathbb{Z}\to \mathbb{R}/\mathbb{Z}$
to be
![]() $\phi_i(x) = a_ix - a_iy + \alpha$
where
$\phi_i(x) = a_ix - a_iy + \alpha$
where
![]() $\alpha$
is an irrational which is smaller than
$\alpha$
is an irrational which is smaller than
![]() $(2K)^{-1}$
and
$(2K)^{-1}$
and
![]() $a_i\in S$
.
$a_i\in S$
.
Note that
![]() $y + B$
is exactly the set
$y + B$
is exactly the set
Note that the set
is measurable with respect to the factor
![]() $\bigvee_{1\le j\le d}\mathcal{B}_{\phi_j,K}$
. Also,
$\bigvee_{1\le j\le d}\mathcal{B}_{\phi_j,K}$
. Also,
![]() $T_2\subseteq T_1$
since
$T_2\subseteq T_1$
since
![]() $|\alpha|\le 1/(2K)$
and
$|\alpha|\le 1/(2K)$
and
![]() $(2K)^{-1}\cdot (2\lfloor K \rho\rfloor-1) + (2K)^{-1}\le\rho$
. Furthermore we have
$(2K)^{-1}\cdot (2\lfloor K \rho\rfloor-1) + (2K)^{-1}\le\rho$
. Furthermore we have
and thus we have
as long as
![]() $8K\le N$
. Here we have used that
$8K\le N$
. Here we have used that
![]() $S\subseteq\mathbb{Z}/N\mathbb{Z}$
where N is prime.
$S\subseteq\mathbb{Z}/N\mathbb{Z}$
where N is prime.
So, since C ′ is large with respect to C and f is 1-bounded we have
The locally cubic function we will consider is
![]() $\phi^{\ast}\colon T_2\to \mathbb{R}/\mathbb{Z}$
given by
$\phi^{\ast}\colon T_2\to \mathbb{R}/\mathbb{Z}$
given by
![]() $\phi^{\ast}(x) = \phi(x) + \alpha$
. This is well-defined as
$\phi^{\ast}(x) = \phi(x) + \alpha$
. This is well-defined as
![]() $T_2\subseteq T_1 = y+B$
. Let
$T_2\subseteq T_1 = y+B$
. Let
![]() $\mathcal{B} = \bigvee_{1\le j\le d}\mathcal{B}_{\phi_j,K} \vee \mathcal{B}_{\phi^\ast,K}$
and note that
$\mathcal{B} = \bigvee_{1\le j\le d}\mathcal{B}_{\phi_j,K} \vee \mathcal{B}_{\phi^\ast,K}$
and note that
since
![]() $z\mapsto e(z)$
is a
$z\mapsto e(z)$
is a
![]() $2\pi$
-Lipschitz function on
$2\pi$
-Lipschitz function on
![]() $\mathbb{R}/\mathbb{Z}$
. Therefore
$\mathbb{R}/\mathbb{Z}$
. Therefore
![]() $\Pi_{\mathcal{B}}$
is self-adjoint with respect to the standard inner product (see e.g. [
Reference Peluse and Prendiville25
, lemma 4·3(ii)]) so
$\Pi_{\mathcal{B}}$
is self-adjoint with respect to the standard inner product (see e.g. [
Reference Peluse and Prendiville25
, lemma 4·3(ii)]) so
This gives the desired result.
We now prove an associated Koopman–von Neumann theorem; our proof is closely modeled after [ Reference Green and Tao13 , theorem 5·6].
Lemma 3·4. There exists
![]() $C \gt 0$
such that the following holds. Fix
$C \gt 0$
such that the following holds. Fix
![]() $\eta \gt 0$
, let f be a function
$\eta \gt 0$
, let f be a function
![]() $f\colon\mathbb{Z}/N\mathbb{Z}\to [0,1]$
, and let
$f\colon\mathbb{Z}/N\mathbb{Z}\to [0,1]$
, and let
![]() $\mathcal{B}^{\ast}$
denote an initial factor.
$\mathcal{B}^{\ast}$
denote an initial factor.
Let
![]() $M(\eta) = \exp\!(\!\log\!(1/\eta)^C)$
and let
$M(\eta) = \exp\!(\!\log\!(1/\eta)^C)$
and let
![]() $N\ge 10 M(\eta)$
. There exist
$N\ge 10 M(\eta)$
. There exist
![]() $d_1,d_2\le M(\eta)$
such that the following holds. There exists an integer
$d_1,d_2\le M(\eta)$
such that the following holds. There exists an integer
![]() $K\le M(\eta)$
and a factor of
$K\le M(\eta)$
and a factor of
![]() $\mathcal{B}'$
of complexity
$\mathcal{B}'$
of complexity
![]() $(d_1,d_2)$
and resolution K such that if
$(d_1,d_2)$
and resolution K such that if
![]() $\mathcal{B} = \mathcal{B}^{\ast} \vee \mathcal{B}'$
then
$\mathcal{B} = \mathcal{B}^{\ast} \vee \mathcal{B}'$
then
Proof. We create the factor
![]() $\mathcal{B}'$
as a join given by applying Lemma 3·3 iteratively. Set
$\mathcal{B}'$
as a join given by applying Lemma 3·3 iteratively. Set
![]() $\mathcal{B}_0 = \mathcal{B}^{\ast}$
.
$\mathcal{B}_0 = \mathcal{B}^{\ast}$
.
-
(i) If
 $\lVert f-\Pi_{\mathcal{B}_i} f\rVert_{U^4(\mathbb{Z}/N\mathbb{Z})}\le \eta$
, we terminate. Set
$\lVert f-\Pi_{\mathcal{B}_i} f\rVert_{U^4(\mathbb{Z}/N\mathbb{Z})}\le \eta$
, we terminate. Set
 $i^{\ast} = i$
and output
$i^{\ast} = i$
and output
 $\mathcal{B}'=\bigvee_{0\le i' \lt i^\ast}\mathcal{B}_{i'}'$
.
$\mathcal{B}'=\bigvee_{0\le i' \lt i^\ast}\mathcal{B}_{i'}'$
. -
(ii) If
 $\lVert f-\Pi_{\mathcal{B}_i} f\rVert_{U^4(\mathbb{Z}/N\mathbb{Z})}\ge \eta$
, then set
$\lVert f-\Pi_{\mathcal{B}_i} f\rVert_{U^4(\mathbb{Z}/N\mathbb{Z})}\ge \eta$
, then set
 $K = \lceil \exp\!(M(\eta))\rceil$
. By Lemma 3·3 there exists
$K = \lceil \exp\!(M(\eta))\rceil$
. By Lemma 3·3 there exists
 $\mathcal{B}_i'$
such that Here
$\mathcal{B}_i'$
such that Here \[\lVert\Pi_{\mathcal{B}_i'}(f-\Pi_{\mathcal{B}_i} f)\rVert_{L^1(\mathbb{Z}/N\mathbb{Z})}\ge \exp\!(\!-\!(\!\log\!(1/\eta))^{C'}).\]
\[\lVert\Pi_{\mathcal{B}_i'}(f-\Pi_{\mathcal{B}_i} f)\rVert_{L^1(\mathbb{Z}/N\mathbb{Z})}\ge \exp\!(\!-\!(\!\log\!(1/\eta))^{C'}).\]
 $\mathcal{B}_i' = \bigvee_{1\le j\le d_i}\mathcal{B}_{\phi_j^{(i)},K} \vee \mathcal{B}_{\phi_i',K}$
where
$\mathcal{B}_i' = \bigvee_{1\le j\le d_i}\mathcal{B}_{\phi_j^{(i)},K} \vee \mathcal{B}_{\phi_i',K}$
where
 $\phi_j^{(i)}$
(for
$\phi_j^{(i)}$
(for
 $j\le d_i\le\exp\!((\!\log\!(1/\eta))^{O(1)}))$
) are irrational linear functions on
$j\le d_i\le\exp\!((\!\log\!(1/\eta))^{O(1)}))$
) are irrational linear functions on
 $\mathbb{Z}/N\mathbb{Z}$
and
$\mathbb{Z}/N\mathbb{Z}$
and
 $\phi_i'$
is a locally cubic function respecting the factor
$\phi_i'$
is a locally cubic function respecting the factor
 $\bigvee_{1\le j\le d}\mathcal{B}_{\phi_j,K}$
. We set
$\bigvee_{1\le j\le d}\mathcal{B}_{\phi_j,K}$
. We set
 $\mathcal{B}_{i+1} = \mathcal{B}_i\vee \mathcal{B}_i'$
.
$\mathcal{B}_{i+1} = \mathcal{B}_i\vee \mathcal{B}_i'$
.
Note that
![]() $\mathcal{B}=\mathcal{B}^\ast\vee\mathcal{B}'=\mathcal{B}_{i^\ast}$
. Observe that
$\mathcal{B}=\mathcal{B}^\ast\vee\mathcal{B}'=\mathcal{B}_{i^\ast}$
. Observe that
 \begin{align*}\lVert\Pi_{\mathcal{B}_i'}(f-\Pi_{\mathcal{B}_i}f)\rVert_{L^1(\mathbb{Z}/N\mathbb{Z})}&\le\lVert\Pi_{\mathcal{B}_i'}(f-\Pi_{\mathcal{B}_i}f)\rVert_{L^2(\mathbb{Z}/N\mathbb{Z})}=\lVert\Pi_{\mathcal{B}_i'}\Pi_{\mathcal{B}_{i+1}}(f-\Pi_{\mathcal{B}_i}f)\rVert_{L^2(\mathbb{Z}/N\mathbb{Z})}\\&\le\lVert\Pi_{\mathcal{B}_{i+1}}(f-\Pi_{\mathcal{B}_i}f)\rVert_{L^2(\mathbb{Z}/N\mathbb{Z})}=\lVert\Pi_{\mathcal{B}_{i+1}}f-\Pi_{\mathcal{B}_i}f\rVert_{L^2(\mathbb{Z}/N\mathbb{Z})}\\&=(\lVert\Pi_{\mathcal{B}_{i+1}}f\rVert_{L^2(\mathbb{Z}/N\mathbb{Z})}^2-\lVert\Pi_{\mathcal{B}_i}f\rVert_{L^2(\mathbb{Z}/N\mathbb{Z})}^2)^{1/2}.\end{align*}
\begin{align*}\lVert\Pi_{\mathcal{B}_i'}(f-\Pi_{\mathcal{B}_i}f)\rVert_{L^1(\mathbb{Z}/N\mathbb{Z})}&\le\lVert\Pi_{\mathcal{B}_i'}(f-\Pi_{\mathcal{B}_i}f)\rVert_{L^2(\mathbb{Z}/N\mathbb{Z})}=\lVert\Pi_{\mathcal{B}_i'}\Pi_{\mathcal{B}_{i+1}}(f-\Pi_{\mathcal{B}_i}f)\rVert_{L^2(\mathbb{Z}/N\mathbb{Z})}\\&\le\lVert\Pi_{\mathcal{B}_{i+1}}(f-\Pi_{\mathcal{B}_i}f)\rVert_{L^2(\mathbb{Z}/N\mathbb{Z})}=\lVert\Pi_{\mathcal{B}_{i+1}}f-\Pi_{\mathcal{B}_i}f\rVert_{L^2(\mathbb{Z}/N\mathbb{Z})}\\&=(\lVert\Pi_{\mathcal{B}_{i+1}}f\rVert_{L^2(\mathbb{Z}/N\mathbb{Z})}^2-\lVert\Pi_{\mathcal{B}_i}f\rVert_{L^2(\mathbb{Z}/N\mathbb{Z})}^2)^{1/2}.\end{align*}
The final equality is the Pythagorean theorem with respect to projections (this follows from e.g. [ Reference Peluse and Prendiville25 , lemma 4·3(iv)]).
Thus
![]() $\lVert\Pi_{\mathcal{B}_{i+1}f}\rVert_{L^2(\mathbb{Z}/N\mathbb{Z})}^2-\lVert\Pi_{\mathcal{B}_i}f\rVert_{L^2(\mathbb{Z}/N\mathbb{Z})}^2\ge \exp\!(\!-\!(\!\log\!(1/\eta))^{O(1)})$
and hence the iteration lasts only
$\lVert\Pi_{\mathcal{B}_{i+1}f}\rVert_{L^2(\mathbb{Z}/N\mathbb{Z})}^2-\lVert\Pi_{\mathcal{B}_i}f\rVert_{L^2(\mathbb{Z}/N\mathbb{Z})}^2\ge \exp\!(\!-\!(\!\log\!(1/\eta))^{O(1)})$
and hence the iteration lasts only
![]() $\exp\!((\!\log\!(1/\eta))^{O(1)})$
steps. Therefore the final
$\exp\!((\!\log\!(1/\eta))^{O(1)})$
steps. Therefore the final
![]() $\mathcal{B}'$
is generated by at most
$\mathcal{B}'$
is generated by at most
![]() $\exp\!((\!\log\!(1/\eta))^{O(1)})$
linear functions and a similar number of locally cubic functions. This completes the proof.
$\exp\!((\!\log\!(1/\eta))^{O(1)})$
linear functions and a similar number of locally cubic functions. This completes the proof.
3·2. Density increment onto cubic Bohr set
We next need that
![]() $\Lambda$
is controlled by the
$\Lambda$
is controlled by the
![]() $U^4$
-norm and the
$U^4$
-norm and the
![]() $L^{1}$
-norm. The proof is by now standard and hence is omitted (see [
Reference Green and Tao13
, lemma 3·2] and [
Reference Gowers9
, theorem 3·2]).
$L^{1}$
-norm. The proof is by now standard and hence is omitted (see [
Reference Green and Tao13
, lemma 3·2] and [
Reference Gowers9
, theorem 3·2]).
Lemma 3·5. Let N be prime and
![]() $f_i\colon\mathbb{Z}/N\mathbb{Z}\to \mathbb{C}$
. Then we have:
$f_i\colon\mathbb{Z}/N\mathbb{Z}\to \mathbb{C}$
. Then we have:
 \begin{align*}|\Lambda(f_1,f_2,f_3,f_4,f_5)|&\le \min_{1\le i\le 5}\lVert f_i\rVert_{L^1(\mathbb{Z}/N\mathbb{Z})}\prod_{j\neq i}\lVert f_j\rVert_{L^\infty(\mathbb{Z}/N\mathbb{Z})};\\|\Lambda(f_1,f_2,f_3,f_4,f_5)|&\le \min_{1\le i \le 5}\lVert f_i\rVert_{U^4(\mathbb{Z}/N\mathbb{Z})}\prod_{j\neq i}\lVert f_j\rVert_{L^\infty(\mathbb{Z}/N\mathbb{Z})}.\end{align*}
\begin{align*}|\Lambda(f_1,f_2,f_3,f_4,f_5)|&\le \min_{1\le i\le 5}\lVert f_i\rVert_{L^1(\mathbb{Z}/N\mathbb{Z})}\prod_{j\neq i}\lVert f_j\rVert_{L^\infty(\mathbb{Z}/N\mathbb{Z})};\\|\Lambda(f_1,f_2,f_3,f_4,f_5)|&\le \min_{1\le i \le 5}\lVert f_i\rVert_{U^4(\mathbb{Z}/N\mathbb{Z})}\prod_{j\neq i}\lVert f_j\rVert_{L^\infty(\mathbb{Z}/N\mathbb{Z})}.\end{align*}
Given this we may now prove that there exists a density increment onto a piece of the partition given by Lemma 3·4. The proof is identical to [ Reference Green and Tao13 , lemma 5·8].
Proposition 3·6. Fix
![]() $c \gt 0$
. There exist
$c \gt 0$
. There exist
![]() $C \gt 0$
and
$C \gt 0$
and
![]() $c' \gt 0$
such that the following holds. Given a function
$c' \gt 0$
such that the following holds. Given a function
![]() $f\colon[N']\to[0,1]$
such that
$f\colon[N']\to[0,1]$
such that
![]() $\mathbb{E}_{n\in[N']}f(n) = \delta \gt 0$
, extend it by 0s to a function on
$\mathbb{E}_{n\in[N']}f(n) = \delta \gt 0$
, extend it by 0s to a function on
![]() $\mathbb{Z}/N\mathbb{Z}$
where N is prime with
$\mathbb{Z}/N\mathbb{Z}$
where N is prime with
![]() $1024N'\le N\le 2048N'$
. Suppose that
$1024N'\le N\le 2048N'$
. Suppose that
Let
![]() $\mathcal{B}^{\ast} = [N']\sqcup ((\mathbb{Z}/N\mathbb{Z})\setminus [N'])$
be an initial factor. Let
$\mathcal{B}^{\ast} = [N']\sqcup ((\mathbb{Z}/N\mathbb{Z})\setminus [N'])$
be an initial factor. Let
![]() $M(\delta) = \exp\!((\!\log\!(1/\delta))^C)$
and suppose that
$M(\delta) = \exp\!((\!\log\!(1/\delta))^C)$
and suppose that
![]() $N\ge M(\delta)$
. Then there exist
$N\ge M(\delta)$
. Then there exist
![]() $d_1,d_2,K\le M(\delta)$
, a factor
$d_1,d_2,K\le M(\delta)$
, a factor
![]() $\mathcal{B}$
of complexity
$\mathcal{B}$
of complexity
![]() $(d_1,d_2)$
and resolution K, and an atom
$(d_1,d_2)$
and resolution K, and an atom
![]() $\Omega^\ast$
of
$\Omega^\ast$
of
![]() $\mathcal{B}\vee\mathcal{B}^{\ast}$
such that:
$\mathcal{B}\vee\mathcal{B}^{\ast}$
such that:
-
(i)
 $\mathbb{P}_{n\in \mathbb{Z}/N\mathbb{Z}}[n\in\Omega^\ast]\ge \exp\!(\!-\!\exp\!((\!\log\!(1/\delta))^C))$
;
$\mathbb{P}_{n\in \mathbb{Z}/N\mathbb{Z}}[n\in\Omega^\ast]\ge \exp\!(\!-\!\exp\!((\!\log\!(1/\delta))^C))$
; -
(ii)
 $\mathbb{E}[f(n)|n\in\Omega^\ast]\ge (1+c')\delta$
.
$\mathbb{E}[f(n)|n\in\Omega^\ast]\ge (1+c')\delta$
.
Proof. We may clearly assume
![]() $\delta$
is sufficiently small. By Lemma 3·4, there exists a factor
$\delta$
is sufficiently small. By Lemma 3·4, there exists a factor
![]() $\mathcal{B}$
of complexity
$\mathcal{B}$
of complexity
![]() $(d_1,d_2)$
and resolution K with
$(d_1,d_2)$
and resolution K with
![]() $d_1,d_2,K\le \exp\!((\!\log\!(1/\delta))^{O(1)})$
such that
$d_1,d_2,K\le \exp\!((\!\log\!(1/\delta))^{O(1)})$
such that
By telescoping and the second part of Lemma 3·5 we have
Therefore we have
Let
![]() $\mathcal{B}' = \mathcal{B}\vee \mathcal{B}^{\ast}$
and
$\mathcal{B}' = \mathcal{B}\vee \mathcal{B}^{\ast}$
and
![]() $g = \min(\Pi_{\mathcal{B}'}f,(1+c')\delta)$
and assume that
$g = \min(\Pi_{\mathcal{B}'}f,(1+c')\delta)$
and assume that
![]() $c'\le \max(c,1)/10^{5}$
. Let
$c'\le \max(c,1)/10^{5}$
. Let
![]() $\Omega' = \{x\in\mathbb{Z}/N\mathbb{Z}\colon g(x)\neq \Pi_{\mathcal{B}'}f(x)\}$
and notice that
$\Omega' = \{x\in\mathbb{Z}/N\mathbb{Z}\colon g(x)\neq \Pi_{\mathcal{B}'}f(x)\}$
and notice that
 \begin{align*}|\Lambda(\Pi_{\mathcal{B}'}f) - \Lambda(g)|&\le 5\lVert\Pi_{\mathcal{B}'}f - g\rVert_{L^1(\mathbb{Z}/N\mathbb{Z})} \le 5 \mathbb{P}[n\in \Omega']\\|\Lambda(\delta\mathbb{1}_{[N']}) - \Lambda(g)|&\le 5(1+c')^4\delta^{4}\lVert\delta\mathbb{1}_{[N']}-g\rVert_{L^1(\mathbb{Z}/N\mathbb{Z})}\\\lVert g - \delta \mathbb{1}_{[N']}\rVert_{L^1(\mathbb{Z}/N\mathbb{Z})}&\le \mathbb{P}[n\in \Omega'] + \lVert\delta \mathbb{1}_{[N']} - \Pi_{\mathcal{B}'}f\rVert_{L^1(\mathbb{Z}/N\mathbb{Z})}.\end{align*}
\begin{align*}|\Lambda(\Pi_{\mathcal{B}'}f) - \Lambda(g)|&\le 5\lVert\Pi_{\mathcal{B}'}f - g\rVert_{L^1(\mathbb{Z}/N\mathbb{Z})} \le 5 \mathbb{P}[n\in \Omega']\\|\Lambda(\delta\mathbb{1}_{[N']}) - \Lambda(g)|&\le 5(1+c')^4\delta^{4}\lVert\delta\mathbb{1}_{[N']}-g\rVert_{L^1(\mathbb{Z}/N\mathbb{Z})}\\\lVert g - \delta \mathbb{1}_{[N']}\rVert_{L^1(\mathbb{Z}/N\mathbb{Z})}&\le \mathbb{P}[n\in \Omega'] + \lVert\delta \mathbb{1}_{[N']} - \Pi_{\mathcal{B}'}f\rVert_{L^1(\mathbb{Z}/N\mathbb{Z})}.\end{align*}
The first and second inequality follow from the first part of Lemma 3·5 while the final inequality follows from the triangle inequality.
Suppose that the proposition is false. Note that there are at most
![]() $2(2K)^{d_1+d_2}$
atoms of
$2(2K)^{d_1+d_2}$
atoms of
![]() $\mathcal{B}'$
and define an atom to be small if it has measure at most
$\mathcal{B}'$
and define an atom to be small if it has measure at most
![]() $(2K)^{-d_1-d_2}\cdot (c\delta^{5})/40$
. We therefore have that on every atom which is not small,
$(2K)^{-d_1-d_2}\cdot (c\delta^{5})/40$
. We therefore have that on every atom which is not small,
(else we take
![]() $\Omega^\ast$
to be that atom) and therefore
$\Omega^\ast$
to be that atom) and therefore
![]() $\mathbb{P}[n\in \Omega']\le c\delta^{5}/20$
. Thus by the first inequality above and the triangle inequality we find
$\mathbb{P}[n\in \Omega']\le c\delta^{5}/20$
. Thus by the first inequality above and the triangle inequality we find
By the second inequality, this implies that
By the third inequality we have that
For a function h let
![]() $h_{+} = \max(h,0)$
. For mean zero functions,
$h_{+} = \max(h,0)$
. For mean zero functions,
![]() $\lVert h\rVert_{L^1(\mathbb{Z}/N\mathbb{Z})} = 2\lVert h_{+}\rVert_{L^1(\mathbb{Z}/N\mathbb{Z})}$
. This allows us to derive the contradiction since
$\lVert h\rVert_{L^1(\mathbb{Z}/N\mathbb{Z})} = 2\lVert h_{+}\rVert_{L^1(\mathbb{Z}/N\mathbb{Z})}$
. This allows us to derive the contradiction since
3·3. Density increment onto subprogression
We now finish the argument by partitioning factors in our cubic Bohr partition into long progressions. This is a technical modification of an argument of Green and Tao [ Reference Green and Tao13 ] for multiple quadratics (the case of a single polynomial is handled in Gowers [ Reference Gowers9 ]); as input they must provide, in the case of quadratics, an explicit implicit constant for a result of Schmidt [ Reference Schmidt32 ] which provides recurrence for multiple polynomials mod 1 simultaneously. We require the analogous result for arbitrary degrees.
Proposition 3·7. Fix an integer
![]() $k\ge 1$
. There exist
$k\ge 1$
. There exist
![]() $c = c(k) \gt 0$
such that the following holds. Let
$c = c(k) \gt 0$
such that the following holds. Let
![]() $\alpha_1,\ldots,\alpha_d$
be real numbers. Then
$\alpha_1,\ldots,\alpha_d$
be real numbers. Then
We defer the proof of this input to Appendix B; it is an essentially verbatim copy of [ Reference Green and Tao13 , appendix A].
Proof of Proposition 3·1. Step 1. Setup. Let
![]() $M=\exp\!((\!\log\!(1/\delta))^C)$
where
$M=\exp\!((\!\log\!(1/\delta))^C)$
where
![]() $C \gt 0$
will be chosen later. Let us assume
$C \gt 0$
will be chosen later. Let us assume
![]() $N' \gt \exp\!(M(\delta))$
and
$N' \gt \exp\!(M(\delta))$
and
![]() $|\Lambda(f)-\Lambda(\delta\mathbb{1}_{[N']})| \gt c\delta^5$
. Our aim is to find a progression of length at least
$|\Lambda(f)-\Lambda(\delta\mathbb{1}_{[N']})| \gt c\delta^5$
. Our aim is to find a progression of length at least
![]() $N^{1/M(\delta)}$
where our density is incremented.
$N^{1/M(\delta)}$
where our density is incremented.
Let
![]() $\mathcal{B}^{\ast} = [N']\sqcup ((\mathbb{Z}/N\mathbb{Z})\setminus [N'])$
be an initial factor. Let
$\mathcal{B}^{\ast} = [N']\sqcup ((\mathbb{Z}/N\mathbb{Z})\setminus [N'])$
be an initial factor. Let
![]() $M'(\delta) = \exp\!((\!\log\!(1/\delta))^{C'})$
where C
′ is chosen appropriately so as to apply Proposition 3·6. By assumption we have
$M'(\delta) = \exp\!((\!\log\!(1/\delta))^{C'})$
where C
′ is chosen appropriately so as to apply Proposition 3·6. By assumption we have
![]() $N\ge M'(\delta)$
. So there exist
$N\ge M'(\delta)$
. So there exist
![]() $d_1,d_2,K\le M'(\delta)$
, a factor
$d_1,d_2,K\le M'(\delta)$
, a factor
![]() $\mathcal{B}$
of complexity
$\mathcal{B}$
of complexity
![]() $(d_1,d_2)$
and resolution K, and an atom
$(d_1,d_2)$
and resolution K, and an atom
![]() $\Omega^\ast$
of
$\Omega^\ast$
of
![]() $\mathcal{B}\vee\mathcal{B}^{\ast}$
such that:
$\mathcal{B}\vee\mathcal{B}^{\ast}$
such that:
-
(i)
 $\mathbb{P}_{n\in \mathbb{Z}/N\mathbb{Z}}[n\in\Omega^\ast]\ge\exp\!(\!-\!\exp\!((\!\log\!(1/\delta))^{C'}))$
;
$\mathbb{P}_{n\in \mathbb{Z}/N\mathbb{Z}}[n\in\Omega^\ast]\ge\exp\!(\!-\!\exp\!((\!\log\!(1/\delta))^{C'}))$
; -
(ii)
 $\mathbb{E}[f(n)|n\in\Omega^\ast]\ge(1+2c')\delta$
.
$\mathbb{E}[f(n)|n\in\Omega^\ast]\ge(1+2c')\delta$
.
Now our aim is to partition
![]() $\Omega^\ast$
into few arithmetic progressions, namely at most
$\Omega^\ast$
into few arithmetic progressions, namely at most
![]() $X=7^dN^{1-\Omega(1/d^7)}$
progressions where
$X=7^dN^{1-\Omega(1/d^7)}$
progressions where
![]() $d=M'(\delta)$
. The number of elements of
$d=M'(\delta)$
. The number of elements of
![]() $\Omega^\ast$
in progressions of length at most
$\Omega^\ast$
in progressions of length at most
![]() $c' \delta |\Omega^\ast|/X$
is at most
$c' \delta |\Omega^\ast|/X$
is at most
![]() $c'\delta|\Omega^\ast|$
. Letting the union of short progressions be
$c'\delta|\Omega^\ast|$
. Letting the union of short progressions be
![]() $\Omega'$
, we have that
$\Omega'$
, we have that
Therefore there is a progression of length longer than
![]() $c' \delta |\Omega^\ast|/X$
with density at least
$c' \delta |\Omega^\ast|/X$
with density at least
![]() $(1+c')\delta$
. We have
$(1+c')\delta$
. We have
due to our assumption
![]() $N' \gt \exp\!(M(\delta))$
, assuming
$N' \gt \exp\!(M(\delta))$
, assuming
![]() $C \gt 0$
is chosen sufficiently large. (This is where the dependence in the first item of Proposition 3·1 comes from.)
$C \gt 0$
is chosen sufficiently large. (This is where the dependence in the first item of Proposition 3·1 comes from.)
We may write
where
![]() $\phi_i$
are linear functions on
$\phi_i$
are linear functions on
![]() $\mathbb{Z}/N\mathbb{Z}$
and
$\mathbb{Z}/N\mathbb{Z}$
and
![]() $\varphi_i\colon T\to\mathbb{R}$
are locally cubic functions on
$\varphi_i\colon T\to\mathbb{R}$
are locally cubic functions on
We additionally have
![]() $|I_1|,|I_2|,K\le M'(\delta)=:d$
. (The fact that
$|I_1|,|I_2|,K\le M'(\delta)=:d$
. (The fact that
![]() $\Omega^\ast\subseteq[N']$
is evident from
$\Omega^\ast\subseteq[N']$
is evident from
![]() $\mathbb{E}[f(n)|n\in\Omega^\ast] \gt 0$
, recalling that f is extended by 0s in Proposition 3·6.)
$\mathbb{E}[f(n)|n\in\Omega^\ast] \gt 0$
, recalling that f is extended by 0s in Proposition 3·6.)
Step 2. Partitioning T into progressions where the cubic phases are near-constant. Our goal will be to partition T into subprogressions on which each
![]() $\varphi_i$
for
$\varphi_i$
for
![]() $i\in I_2$
is roughly constant
$i\in I_2$
is roughly constant
![]() $\mod 1$
. In fact, we will find a collection of progressions, say of the form
$\mod 1$
. In fact, we will find a collection of progressions, say of the form
![]() $\{a+bn\colon n\in[L]\}$
, so that for
$\{a+bn\colon n\in[L]\}$
, so that for
![]() $n\in[L]$
we have
$n\in[L]$
we have
![]() $\varphi_i(a+bn)=\kappa+P_i^{(a,b)}(n)\mod 1$
, where
$\varphi_i(a+bn)=\kappa+P_i^{(a,b)}(n)\mod 1$
, where
![]() $P_i^{(a,b)}$
is a real polynomial of degree at most 3 with coefficients of size
$P_i^{(a,b)}$
is a real polynomial of degree at most 3 with coefficients of size
![]() $O(L^{-4})$
.
$O(L^{-4})$
.
We first partition
where
![]() $T_j$
are progressions and
$T_j$
are progressions and
![]() $|J_1|\ll 2^{|I_1|}N^{1-1/(|I_1|+1)}$
. To do this, we may use [
Reference Green and Tao13
, proposition 6·3] (which is a simple application of Kronecker approximation, or Proposition 3·7 for
$|J_1|\ll 2^{|I_1|}N^{1-1/(|I_1|+1)}$
. To do this, we may use [
Reference Green and Tao13
, proposition 6·3] (which is a simple application of Kronecker approximation, or Proposition 3·7 for
![]() $k=1$
).
$k=1$
).
Since
![]() $T_j$
is a progression, we may write
$T_j$
is a progression, we may write
![]() $T_j=\{a_j+d_j,\ldots,a_j+M_jd_j\}$
, where
$T_j=\{a_j+d_j,\ldots,a_j+M_jd_j\}$
, where
![]() $M_j=|T_j|$
. Since each
$M_j=|T_j|$
. Since each
![]() $\varphi_i$
is locally cubic on this progression, we may write
$\varphi_i$
is locally cubic on this progression, we may write
for
![]() $i\in I_2$
and
$i\in I_2$
and
![]() $n\in[M_j]$
where
$n\in[M_j]$
where
![]() $j\in J_1$
. Next, we perform three intermediate partitions of
$j\in J_1$
. Next, we perform three intermediate partitions of
![]() $T_j$
in order to iteratively “reduce the degree” of the function
$T_j$
in order to iteratively “reduce the degree” of the function
![]() $\varphi_i$
until we see that it is roughly constant on our subprogressions.
$\varphi_i$
until we see that it is roughly constant on our subprogressions.
First, choose
![]() $1\le r_j\le M_j^{1/3}$
so that
$1\le r_j\le M_j^{1/3}$
so that
Then we can partition
![]() $[M_j]$
into at most
$[M_j]$
into at most
![]() $M_j^{1-c(3)/(120d^2)}$
progressions of difference
$M_j^{1-c(3)/(120d^2)}$
progressions of difference
![]() $r_j$
and length roughly
$r_j$
and length roughly
![]() $M_j^{c(3)/(120d^2)}$
. This corresponds to a partition
$M_j^{c(3)/(120d^2)}$
. This corresponds to a partition
with
![]() $|D_3|\le M_j^{1-c(3)/(120d^2)}$
and
$|D_3|\le M_j^{1-c(3)/(120d^2)}$
and
![]() $|T_{j,k_3}|\sim M_j^{c(3)/(120d^2)}$
. Furthermore, we have
$|T_{j,k_3}|\sim M_j^{c(3)/(120d^2)}$
. Furthermore, we have
for some integer
![]() $b_{j,k_3}$
. We have
$b_{j,k_3}$
. We have
 \begin{align*}\varphi_i(a_j+(b_{j,k_3}+r_jn)d_j)&=\alpha_i^{(j)}(b_{j,k_3}+r_jn)^3+\beta_i^{(j)}(b_{j,k_3}+r_jn)^2+\gamma_i^{(j)}(b_{j,k_3}+r_jn)+\delta_i^{(j)}\\&=\alpha_i^{(j,k_3)}n^2+\beta_i^{(j,k_3)}n+\gamma_i^{(j,k_3)}+\{\alpha_i^{(j)}r_j^3\}n^3 \;\mathrm{mod}\;1.\end{align*}
\begin{align*}\varphi_i(a_j+(b_{j,k_3}+r_jn)d_j)&=\alpha_i^{(j)}(b_{j,k_3}+r_jn)^3+\beta_i^{(j)}(b_{j,k_3}+r_jn)^2+\gamma_i^{(j)}(b_{j,k_3}+r_jn)+\delta_i^{(j)}\\&=\alpha_i^{(j,k_3)}n^2+\beta_i^{(j,k_3)}n+\gamma_i^{(j,k_3)}+\{\alpha_i^{(j)}r_j^3\}n^3 \;\mathrm{mod}\;1.\end{align*}
By construction,
![]() $\{\alpha_i^{(j)}r_j^3\}$
is close to
$\{\alpha_i^{(j)}r_j^3\}$
is close to
![]() $0\;\mathrm{mod}\;1$
(namely, it is
$0\;\mathrm{mod}\;1$
(namely, it is
![]() $\ll dM_j^{-c(3)/(3d^2)}\ll|T_{j,k_3}|^{-30}$
).
$\ll dM_j^{-c(3)/(3d^2)}\ll|T_{j,k_3}|^{-30}$
).
We can thus consider the quadratic function obtained by removing this part, and repeat the same process on each
![]() $T_{j,k_3}$
. We obtain iterative decompositions
$T_{j,k_3}$
. We obtain iterative decompositions
 \[T_{j,k_3}=\bigsqcup_{k_2\in D_2^{(k_3)}}T_{j,k_3,k_2},\quad T_{j,k_3,k_2}=\bigsqcup_{k_1\in D_1^{(k_3,k_2)}}T_{j,k_3,k_2,k_1},\]
\[T_{j,k_3}=\bigsqcup_{k_2\in D_2^{(k_3)}}T_{j,k_3,k_2},\quad T_{j,k_3,k_2}=\bigsqcup_{k_1\in D_1^{(k_3,k_2)}}T_{j,k_3,k_2,k_1},\]
where:
 \begin{align*}|D_2^{(k_3)}|\le|T_{j,k_3}|^{1-c(2)/(120d^2)},\quad |D_1^{(k_3,k_2)}|\le|T_{j,k_3,k_2}|^{1-c(1)/(120d^2)};\\|T_{j,k_3,k_2}|\sim|T_{j,k_3}|^{c(2)/(120d^2)},\quad|T_{j,k_3,k_2,k_1}|\sim|T_{j,k_3,k_2}|^{c(1)/(120d^2)}.\end{align*}
\begin{align*}|D_2^{(k_3)}|\le|T_{j,k_3}|^{1-c(2)/(120d^2)},\quad |D_1^{(k_3,k_2)}|\le|T_{j,k_3,k_2}|^{1-c(1)/(120d^2)};\\|T_{j,k_3,k_2}|\sim|T_{j,k_3}|^{c(2)/(120d^2)},\quad|T_{j,k_3,k_2,k_1}|\sim|T_{j,k_3,k_2}|^{c(1)/(120d^2)}.\end{align*}
Additionally, we will find that if
![]() $T_{j,k_3,k_2,k_1}=\{a+bn\colon n\in[|T_{j,k_3,k_2,k_1}|]\}$
then
$T_{j,k_3,k_2,k_1}=\{a+bn\colon n\in[|T_{j,k_3,k_2,k_1}|]\}$
then
where
The number of such
![]() $T_{j,k_3,k_2,k_1}$
partitioning
$T_{j,k_3,k_2,k_1}$
partitioning
![]() $T_j$
is in total at most
$T_j$
is in total at most
(In the rare cases of any j such that
![]() $M_j\le\exp\!(O(d^6))$
we may simply partition
$M_j\le\exp\!(O(d^6))$
we may simply partition
![]() $M_j$
into progressions of length 1 appropriately.)
$M_j$
into progressions of length 1 appropriately.)
Finally, choosing appropriate value
![]() $p=\Omega(1/d^6)$
, the total number of subprogressions is
$p=\Omega(1/d^6)$
, the total number of subprogressions is
 \[\sum_{j\in J_1}M_j^{1-p}\le|J_1|^p\bigg(\sum_{j\in J_1}M_j\bigg)^{1-p}\le|J_1|^pN^{1-p}\le N^{1-\Omega(1/d^7)}.\]
\[\sum_{j\in J_1}M_j^{1-p}\le|J_1|^p\bigg(\sum_{j\in J_1}M_j\bigg)^{1-p}\le|J_1|^pN^{1-p}\le N^{1-\Omega(1/d^7)}.\]
Step 3. Partitioning
![]() $\Omega^\ast$
into few progressions. From the previous part, we have a partition of T into at most
$\Omega^\ast$
into few progressions. From the previous part, we have a partition of T into at most
![]() $N^{1-\Omega(1/d^7)}$
progressions of various lengths so that for a progression
$N^{1-\Omega(1/d^7)}$
progressions of various lengths so that for a progression
![]() $\{a+bn\colon n\in[L]\}$
that appears, we have
$\{a+bn\colon n\in[L]\}$
that appears, we have
where
![]() $P_i^{(a,b)}$
is a real polynomial of degree at most 3 with coefficients of size
$P_i^{(a,b)}$
is a real polynomial of degree at most 3 with coefficients of size
![]() $O(L^{-4})$
. Recalling
$O(L^{-4})$
. Recalling
![]() $\Omega^\ast\subseteq T$
, we can now intersect these progressions with
$\Omega^\ast\subseteq T$
, we can now intersect these progressions with
![]() $\Omega^\ast$
. Note that
$\Omega^\ast$
. Note that
![]() $\Omega^\ast$
merely imposes a condition on each
$\Omega^\ast$
merely imposes a condition on each
![]() $\varphi_i$
for
$\varphi_i$
for
![]() $i\in I_2$
. Since each
$i\in I_2$
. Since each
![]() $P_i^{(a,b)}(n)$
is at most degree 3, within the range
$P_i^{(a,b)}(n)$
is at most degree 3, within the range
![]() $n\in[L]$
it hits the cutoffs for the condition for
$n\in[L]$
it hits the cutoffs for the condition for
![]() $\varphi_i$
at most
$\varphi_i$
at most
![]() $2\cdot 3=6$
times in the real numbers. Since
$2\cdot 3=6$
times in the real numbers. Since
![]() $P_i^{(a,b)}(n)$
has small coefficients (so is small on
$P_i^{(a,b)}(n)$
has small coefficients (so is small on
![]() $n\in[L]$
), there is no rounding wraparound and the same holds for its image
$n\in[L]$
), there is no rounding wraparound and the same holds for its image
![]() $\;\mathrm{mod}\;1$
over the domain
$\;\mathrm{mod}\;1$
over the domain
![]() $n\in[L]$
.
$n\in[L]$
.
The upshot is that each progression is cut into at most 7 pieces by the condition on
![]() $\varphi_i$
defining
$\varphi_i$
defining
![]() $\Omega^\ast$
for each
$\Omega^\ast$
for each
![]() $i\in I_2$
. This gives at most
$i\in I_2$
. This gives at most
![]() $7^{|I_2|}\le 7^d$
total pieces.
$7^{|I_2|}\le 7^d$
total pieces.
Thus, we have a partition of
![]() $\Omega^\ast$
into at most
$\Omega^\ast$
into at most
![]() $7^dN^{1-\Omega(1/d^7)}$
pieces, which combined with the argument above completes the proof.
$7^dN^{1-\Omega(1/d^7)}$
pieces, which combined with the argument above completes the proof.
Appendix A. Conventions regarding nilsequences and effective equidistribution
We begin this appendix by giving the precise definition of the complexity of a nilmanifold; this definition is exactly as in [ Reference Tao and Teräväinen37 , definition 6·1].
Definition A·1. Let
![]() $s\ge 1$
be an integer and let
$s\ge 1$
be an integer and let
![]() $K \gt 0$
. A filtered nilmanifold
$K \gt 0$
. A filtered nilmanifold
![]() $G/\Gamma$
of degree s and complexity at most K consists of the following:
$G/\Gamma$
of degree s and complexity at most K consists of the following:
-
(i) a nilpotent, connected, and simply connected Lie group G of dimension m, which can be identified with its Lie algebra
 $\log G$
via the exponential map
$\log G$
via the exponential map
 $\exp\colon\log G\to G$
;
$\exp\colon\log G\to G$
; -
(ii) a filtration
 $G_{\bullet} = (G_i)_{i\ge 0}$
of closed connected subgroups
$G_{\bullet} = (G_i)_{i\ge 0}$
of closed connected subgroups
 $G_i$
of G with such that
$G_i$
of G with such that \[G = G_0 = G_1\geqslant G_1\geqslant \cdots\geqslant G_s\geqslant G_{s+1} = \mathrm{Id}_G\]
\[G = G_0 = G_1\geqslant G_1\geqslant \cdots\geqslant G_s\geqslant G_{s+1} = \mathrm{Id}_G\]
 $[G_i,G_j]\subseteq G_{i+j}$
for all
$[G_i,G_j]\subseteq G_{i+j}$
for all
 $i,j\ge 0$
(equivalently
$i,j\ge 0$
(equivalently
 $[\log G_i, \log G_j]\subseteq \log G_{i+j}$
);
$[\log G_i, \log G_j]\subseteq \log G_{i+j}$
);
-
(iii) a discrete cocompact subgroup
 $\Gamma$
of G; and
$\Gamma$
of G; and -
(iv) a linear basis
 $\mathcal{X}=\{X_1,\ldots, X_{m}\}$
of
$\mathcal{X}=\{X_1,\ldots, X_{m}\}$
of
 $\log G$
, known as a Mal’cev basis.
$\log G$
, known as a Mal’cev basis.
We, furthermore, require that this data obeys the following conditions:
-
(1) for
 $1\le i,j\le m$
, one has Lie algebra relations for rational numbers
$1\le i,j\le m$
, one has Lie algebra relations for rational numbers \[[X_i,X_j] = \sum_{i,j \lt k\le m}c_{ijk}X_k\]
\[[X_i,X_j] = \sum_{i,j \lt k\le m}c_{ijk}X_k\]
 $c_{ijk}$
of height at most K (we will often refer to these as the Lie bracket structure constants);
$c_{ijk}$
of height at most K (we will often refer to these as the Lie bracket structure constants);
-
(2) for each
 $1\le i\le s$
, the Lie algebra
$1\le i\le s$
, the Lie algebra
 $\log G_i$
is spanned by
$\log G_i$
is spanned by
 $\{X_j\colon m-\dim(G_i) \lt j\le m\}$
; and
$\{X_j\colon m-\dim(G_i) \lt j\le m\}$
; and -
(3) the subgroup
 $\Gamma$
consists of all elements of the form
$\Gamma$
consists of all elements of the form
 $\exp\!(t_1X_1)\cdots\exp\!(t_{m}X_{m})$
with
$\exp\!(t_1X_1)\cdots\exp\!(t_{m}X_{m})$
with
 $t_i\in \mathbb{Z}$
.
$t_i\in \mathbb{Z}$
.
We note that the conditions imply
![]() $[G,G_s]=\mathrm{Id}_G$
, i.e.,
$[G,G_s]=\mathrm{Id}_G$
, i.e.,
![]() $G_s$
is contained in the center of G (commutes with every element).
$G_s$
is contained in the center of G (commutes with every element).
Next, we will define polynomial sequences in filtered nilpotent groups. This concrete definition is equivalent (by [ Reference Green and Tao11 , lemma 6·7]) to the one given in [ Reference Green and Tao11 ].
Definition A·2. We adopt the conventions of Definition A·1. Let G be a filtered nilpotent group of degree s. A function
![]() $g\colon\mathbb{Z}\to G$
is a polynomial sequence if there exist elements
$g\colon\mathbb{Z}\to G$
is a polynomial sequence if there exist elements
![]() $g_i\in G_{i}$
for
$g_i\in G_{i}$
for
![]() $i=0,\ldots,s$
such that
$i=0,\ldots,s$
such that
where
![]() $\binom{n}{i}={1}/{i!}\prod_{j=0}^{i-1}(n-j)$
, for all
$\binom{n}{i}={1}/{i!}\prod_{j=0}^{i-1}(n-j)$
, for all
![]() $n\in\mathbb{Z}$
. We say a polynomial sequence g(n) is N-periodic with respect to a lattice
$n\in\mathbb{Z}$
. We say a polynomial sequence g(n) is N-periodic with respect to a lattice
![]() $\Gamma$
if
$\Gamma$
if
for all
![]() $n\in \mathbb{Z}$
.
$n\in \mathbb{Z}$
.
We will denote the set of polynomial sequences
![]() $g\colon\mathbb{Z}\to G$
relative to the filtration
$g\colon\mathbb{Z}\to G$
relative to the filtration
![]() $G_\bullet$
of G by
$G_\bullet$
of G by
![]() $\operatorname{poly}(\mathbb{Z},G_\bullet)$
. It turns out that
$\operatorname{poly}(\mathbb{Z},G_\bullet)$
. It turns out that
![]() $\operatorname{poly}(\mathbb{Z},G_\bullet)$
is a group under the natural multiplication of sequences–this is due to Lazard [
Reference Lazard19
] and Leibman [
Reference Leibman20, Reference Leibman21
].
$\operatorname{poly}(\mathbb{Z},G_\bullet)$
is a group under the natural multiplication of sequences–this is due to Lazard [
Reference Lazard19
] and Leibman [
Reference Leibman20, Reference Leibman21
].
Now we can define Mal’cev coordinates, the explicit metrics on G and
![]() $G/\Gamma$
used in our work, and the precise definition of the Lipschitz norm of functions on
$G/\Gamma$
used in our work, and the precise definition of the Lipschitz norm of functions on
![]() $G/\Gamma$
. These definitions are exactly as in [
Reference Green and Tao11
, appendix A].
$G/\Gamma$
. These definitions are exactly as in [
Reference Green and Tao11
, appendix A].
Definition A·3. We adopt the conventions of Definition A·1. Given a Mal’cev basis
![]() $\mathcal{X}$
and
$\mathcal{X}$
and
![]() $g\in G$
, there exists
$g\in G$
, there exists
![]() $(t_1,\ldots,t_m)\in \mathbb{R}^{m}$
such that
$(t_1,\ldots,t_m)\in \mathbb{R}^{m}$
such that
We define Mal’cev coordinates of first kind
![]() $\psi_{\exp}=\psi_{\exp,\mathcal{X}}\colon G\to\mathbb{R}^m$
for g relative to
$\psi_{\exp}=\psi_{\exp,\mathcal{X}}\colon G\to\mathbb{R}^m$
for g relative to
![]() $\mathcal{X}$
by
$\mathcal{X}$
by
Given
![]() $g\in G$
there also exists
$g\in G$
there also exists
![]() $(u_1,\ldots,u_m)\in \mathbb{R}^m$
such that
$(u_1,\ldots,u_m)\in \mathbb{R}^m$
such that
and we define the Mal’cev coordinates of second kind
![]() $\psi=\psi_{\mathcal{X}}\colon G\to\mathbb{R}^m$
for g relative to
$\psi=\psi_{\mathcal{X}}\colon G\to\mathbb{R}^m$
for g relative to
![]() $\mathcal{X}$
by
$\mathcal{X}$
by
We then define a metric
![]() $d = d_{\mathcal{X}}$
on G by
$d = d_{\mathcal{X}}$
on G by
 \begin{align*} & d(x,y) \;:\!=\;\\[5pt] & \inf\bigg\{\sum_{i=1}^{n}\min(\lVert\psi(x_ix_{i+1}^{-1})\rVert,\lVert\psi(x_{i+1}x_{i}^{-1})\rVert)\colon n\in\mathbb{N}, x_1,\ldots,x_{n+1}\in G, x_1 = x, x_{n+1} = y\bigg\},\end{align*}
\begin{align*} & d(x,y) \;:\!=\;\\[5pt] & \inf\bigg\{\sum_{i=1}^{n}\min(\lVert\psi(x_ix_{i+1}^{-1})\rVert,\lVert\psi(x_{i+1}x_{i}^{-1})\rVert)\colon n\in\mathbb{N}, x_1,\ldots,x_{n+1}\in G, x_1 = x, x_{n+1} = y\bigg\},\end{align*}
where
![]() $\lVert\cdot\rVert$
denotes the
$\lVert\cdot\rVert$
denotes the
![]() $\ell^\infty$
-norm on
$\ell^\infty$
-norm on
![]() $\mathbb{R}^m$
, and define a metric on
$\mathbb{R}^m$
, and define a metric on
![]() $G/\Gamma$
by
$G/\Gamma$
by
Furthermore, for any function
![]() $F\colon G/\Gamma\to\mathbb{C}$
, we define
$F\colon G/\Gamma\to\mathbb{C}$
, we define
 \[\lVert F\rVert_{\mathrm{Lip}} \;:\!=\; \lVert F\rVert_{\infty} + \sup_{\substack{x,y\in G/\Gamma \\ x\neq y}}\frac{|F(x)-F(y)|}{d(x,y)}.\]
\[\lVert F\rVert_{\mathrm{Lip}} \;:\!=\; \lVert F\rVert_{\infty} + \sup_{\substack{x,y\in G/\Gamma \\ x\neq y}}\frac{|F(x)-F(y)|}{d(x,y)}.\]
We recall the notion of a horizontal character and the notion of a function F having a vertical frequency; our definitions are exactly as in [ Reference Green and Tao11 , definitions 1·5, 3·3, 3·4, 3·5].
Definition A·4. Given a filtered nilmanifold
![]() $G/\Gamma$
, the horizontal torus is defined to be
$G/\Gamma$
, the horizontal torus is defined to be
A horizontal character is a continuous homomorphism
![]() $\eta\colon G\to\mathbb{R}/\mathbb{Z}$
that annihilates
$\eta\colon G\to\mathbb{R}/\mathbb{Z}$
that annihilates
![]() $\Gamma$
; such characters may be equivalently viewed as characters on the horizontal torus. A horizontal character is nontrivial if it is not identically zero.
$\Gamma$
; such characters may be equivalently viewed as characters on the horizontal torus. A horizontal character is nontrivial if it is not identically zero.
Furthermore, if the nilmanifold
![]() $G/\Gamma$
has degree s, the vertical torus is defined to be
$G/\Gamma$
has degree s, the vertical torus is defined to be
A vertical character is a continuous homomorphism
![]() $\xi\colon G_s\to\mathbb{R}/\mathbb{Z}$
that annihilates
$\xi\colon G_s\to\mathbb{R}/\mathbb{Z}$
that annihilates
![]() $\Gamma\cap G_s$
. Setting
$\Gamma\cap G_s$
. Setting
![]() $m_s = \dim G_s$
, one may use the last
$m_s = \dim G_s$
, one may use the last
![]() $m_s$
coordinates of the Mal’cev coordinate map to identify
$m_s$
coordinates of the Mal’cev coordinate map to identify
![]() $G_s$
and
$G_s$
and
![]() $G_s/(G_s\cap \Gamma)$
with
$G_s/(G_s\cap \Gamma)$
with
![]() $\mathbb{R}^{m_s}$
and
$\mathbb{R}^{m_s}$
and
![]() $\mathbb{R}^{m_s}/\mathbb{Z}^{m_s}$
, respectively. Thus, we may identify any vertical character
$\mathbb{R}^{m_s}/\mathbb{Z}^{m_s}$
, respectively. Thus, we may identify any vertical character
![]() $\xi$
with a unique
$\xi$
with a unique
![]() $k\in \mathbb{Z}^{m_s}$
such that
$k\in \mathbb{Z}^{m_s}$
such that
![]() $\xi(x) = k\cdot x$
under this identification
$\xi(x) = k\cdot x$
under this identification
![]() $G_s/(\Gamma\cap G_s) \cong \mathbb{R}^{m_s}/\mathbb{Z}^{m_s}$
. We refer to k as the frequency of the character
$G_s/(\Gamma\cap G_s) \cong \mathbb{R}^{m_s}/\mathbb{Z}^{m_s}$
. We refer to k as the frequency of the character
![]() $\xi$
, we write
$\xi$
, we write
![]() $|\xi| \;:\!=\;\lVert k\rVert_{\infty}$
to denote the magnitude of the frequency
$|\xi| \;:\!=\;\lVert k\rVert_{\infty}$
to denote the magnitude of the frequency
![]() $\xi$
, and say that a function
$\xi$
, and say that a function
![]() $F\colon G/\Gamma\to\mathbb{C}$
has a vertical frequency
$F\colon G/\Gamma\to\mathbb{C}$
has a vertical frequency
![]() $\xi$
if
$\xi$
if
for all
![]() $g_s\in G_s$
and
$g_s\in G_s$
and
![]() $x\in G/\Gamma$
.
$x\in G/\Gamma$
.
Appendix B. Explicit dimension dependence for Schmidt’s polynomial recurrence
We now prove the explicit version of Schmidt’s polynomial recurrence (Proposition 3·7). The proof we provide is essentially verbatim from [ Reference Green and Tao13 , appendix A]. For those familiar with the proof presented there, the use of theta functions is unrelated to the fact that one is finding small fractional parts of quadratic polynomials. Roughly speaking, the theta function is only used as a smooth approximation of the neighbourhood of points in a lattice which has nice Fourier properties.
Definition B·1. Suppose that
![]() $\Lambda$
is a lattice of full rank in
$\Lambda$
is a lattice of full rank in
![]() $\mathbb{R}^d$
. The dual lattice, denoted
$\mathbb{R}^d$
. The dual lattice, denoted
![]() $\Lambda^\ast$
, is
$\Lambda^\ast$
, is
![]() $\Lambda^{\ast} = \{\xi\in \mathbb{R}^d\colon\xi\cdot m\in \mathbb{Z}\text{ for all } m\in \Lambda\}$
. For any
$\Lambda^{\ast} = \{\xi\in \mathbb{R}^d\colon\xi\cdot m\in \mathbb{Z}\text{ for all } m\in \Lambda\}$
. For any
![]() $t \gt 0$
and
$t \gt 0$
and
![]() $x\in \mathbb{R}^d$
, we define
$x\in \mathbb{R}^d$
, we define
Finally define
We next need a version of Weyl’s inequality; we take the statement from [ Reference Green and Tao11 , proposition 4·3].
Proposition B·2. There exists
![]() $C = C(k) \gt 0$
such that the following holds. Suppose that
$C = C(k) \gt 0$
such that the following holds. Suppose that
![]() $g\colon\mathbb{Z}\to\mathbb{R}$
is a polynomial of degree k and
$g\colon\mathbb{Z}\to\mathbb{R}$
is a polynomial of degree k and
![]() $\delta\in(0,1/2)$
. If
$\delta\in(0,1/2)$
. If
![]() $N\ge\delta^{-C}$
and
$N\ge\delta^{-C}$
and
then there exists a positive integer
![]() $\ell$
such that
$\ell$
such that
![]() $\ell\le\delta^{-C}$
and
$\ell\le\delta^{-C}$
and
Remark. For a polynomial
![]() $P(n)=a_0+\cdots+a_kn^k$
, we have
$P(n)=a_0+\cdots+a_kn^k$
, we have
![]() $\lVert P\rVert_{C^\infty[N]}=\max_{0 \lt i\le k}N^i\lVert a_i\rVert_{\mathbb{R}/\mathbb{Z}}$
.
$\lVert P\rVert_{C^\infty[N]}=\max_{0 \lt i\le k}N^i\lVert a_i\rVert_{\mathbb{R}/\mathbb{Z}}$
.
A crucial object of study for
![]() $\alpha\in\mathbb{R}^d$
will be
$\alpha\in\mathbb{R}^d$
will be
the final equality is a consequence of the Poisson summation formula (cf. [ Reference Green and Tao13 , (A·3), (A·5)]).
The following appears as [ Reference Green and Tao13 , lemma A·5 (i),(ii),(iii)] except with trivial modification for the differing degree.
Lemma B·3. Let
![]() $\Lambda$
be a lattice of full rank in
$\Lambda$
be a lattice of full rank in
![]() $\mathbb{R}^d$
, let
$\mathbb{R}^d$
, let
![]() $\alpha\in \mathbb{R}^d$
, and
$\alpha\in \mathbb{R}^d$
, and
![]() $N \gt 0$
. We have the following properties:
$N \gt 0$
. We have the following properties:
-
(i) (contraction on N) For any
 $c\in (10/N,1)$
, we have
$c\in (10/N,1)$
, we have
 $F_{\Lambda,\alpha}(N)\gg cF_{\Lambda,\alpha}(cN)$
;
$F_{\Lambda,\alpha}(N)\gg cF_{\Lambda,\alpha}(cN)$
; -
(ii) (dilation of
 $\alpha$
) For any integer
$\alpha$
) For any integer
 $q\ge 1$
, we have
$q\ge 1$
, we have
 $F_{\Lambda,\alpha}(N)\gg\frac{1}{q} F_{\Lambda,q^k\alpha}(N/q)$
;
$F_{\Lambda,\alpha}(N)\gg\frac{1}{q} F_{\Lambda,q^k\alpha}(N/q)$
; -
(iii) (stability) Suppose that
 $\lVert\widetilde{\alpha}-\alpha\rVert_2\le \varepsilon N^{-k}$
with
$\lVert\widetilde{\alpha}-\alpha\rVert_2\le \varepsilon N^{-k}$
with
 $\varepsilon\in (0,1)$
. Then
$\varepsilon\in (0,1)$
. Then
 $F_{\Lambda,\alpha}(N)\gg F_{(1+\varepsilon)\Lambda,(1+\varepsilon)\widetilde{\alpha}}(N)$
.
$F_{\Lambda,\alpha}(N)\gg F_{(1+\varepsilon)\Lambda,(1+\varepsilon)\widetilde{\alpha}}(N)$
.
Proof. We prove each of the items in turn. For the first item, note that
![]() $\Theta_\Lambda \gt 0$
so
$\Theta_\Lambda \gt 0$
so
For the second item, if
![]() $q \gt N$
note that
$q \gt N$
note that
For
![]() $q\le N$
, we have
$q\le N$
, we have
We now handle the final item; let
![]() $X \;:\!=\; \lVert n^k\alpha -m\rVert_2$
,
$X \;:\!=\; \lVert n^k\alpha -m\rVert_2$
,
![]() $\widetilde{X} = \lVert n^k\widetilde{\alpha}-m\rVert_2$
, and note that
$\widetilde{X} = \lVert n^k\widetilde{\alpha}-m\rVert_2$
, and note that
![]() $|X-\widetilde{X}|\le \lVert n^k(\alpha-\widetilde{\alpha})\rVert_2\le \varepsilon$
. We have that
$|X-\widetilde{X}|\le \lVert n^k(\alpha-\widetilde{\alpha})\rVert_2\le \varepsilon$
. We have that
![]() $4\pi + \pi(1+\varepsilon)^2\widetilde{X}^2\ge \pi X^2$
for all
$4\pi + \pi(1+\varepsilon)^2\widetilde{X}^2\ge \pi X^2$
for all
![]() $X\ge 0$
and
$X\ge 0$
and
![]() $\widetilde{X}\in[X\pm\varepsilon]$
; the inequality is trivial for
$\widetilde{X}\in[X\pm\varepsilon]$
; the inequality is trivial for
![]() $X\le 2$
and for
$X\le 2$
and for
![]() $X\ge 2$
we have that
$X\ge 2$
we have that
![]() $(1+\varepsilon)(X-\varepsilon) - X = \varepsilon (X-(1+\varepsilon))\ge 0$
. Therefore
$(1+\varepsilon)(X-\varepsilon) - X = \varepsilon (X-(1+\varepsilon))\ge 0$
. Therefore
Summing over
![]() $m\in \Lambda$
and
$m\in \Lambda$
and
![]() $|n|\le N$
, the desired result follows.
$|n|\le N$
, the desired result follows.
The key point (which is identical to [
Reference Green and Tao13
, lemma A·6] modulo citing Weyl’s inequality for higher degree polynomials) is noting that if
![]() $F_{\Lambda,\alpha}(N)$
is small then there exists a vector in
$F_{\Lambda,\alpha}(N)$
is small then there exists a vector in
![]() $\Lambda^{\ast}$
which is nearly orthogonal to
$\Lambda^{\ast}$
which is nearly orthogonal to
![]() $\alpha$
.
$\alpha$
.
Lemma B·4. (Schmidt alternative). There exists
![]() $C = C(k) \gt 0$
such that the following holds. Suppose that
$C = C(k) \gt 0$
such that the following holds. Suppose that
![]() $\alpha \in \mathbb{R}^d$
and
$\alpha \in \mathbb{R}^d$
and
![]() $\Lambda\subseteq\mathbb{R}^d$
is a full rank lattice. Let N be a positive integer. Then one of the following always holds:
$\Lambda\subseteq\mathbb{R}^d$
is a full rank lattice. Let N be a positive integer. Then one of the following always holds:
-
(i)
 $F_{\Lambda,\alpha}(N)\ge 1/2$
;
$F_{\Lambda,\alpha}(N)\ge 1/2$
; -
(ii) There exist positive integer
 $q\ll dA_{\Lambda}^C$
and primitive
$q\ll dA_{\Lambda}^C$
and primitive
 $\xi\in \Lambda^{\ast}\setminus \{0\}$
such that
$\xi\in \Lambda^{\ast}\setminus \{0\}$
such that  \[\lVert\xi\rVert_2\ll \sqrt{d} + \sqrt{\log A_{\Lambda}}\text{ and } \lVert q\xi \cdot \alpha\rVert_{\mathbb{R}/\mathbb{Z}}\ll A_{\Lambda}^{C}N^{-k}.\]
\[\lVert\xi\rVert_2\ll \sqrt{d} + \sqrt{\log A_{\Lambda}}\text{ and } \lVert q\xi \cdot \alpha\rVert_{\mathbb{R}/\mathbb{Z}}\ll A_{\Lambda}^{C}N^{-k}.\]
(
![]() $\xi\in\Lambda^\ast$
is primitive if
$\xi\in\Lambda^\ast$
is primitive if
![]() $\xi/n\notin \Lambda^{\ast}$
for all
$\xi/n\notin \Lambda^{\ast}$
for all
![]() $n\ge 2$
.)
$n\ge 2$
.)
Proof. We claim that it suffices to prove that if
![]() $F_{\Lambda,\alpha}(N)\le 1/2$
, then there exists
$F_{\Lambda,\alpha}(N)\le 1/2$
, then there exists
![]() $q\ll A_{\Lambda}^{C}$
and a vector
$q\ll A_{\Lambda}^{C}$
and a vector
Note that the shortest vector in
![]() $\Lambda^{\ast}$
is easily seen to be
$\Lambda^{\ast}$
is easily seen to be
![]() $\gg A_{\Lambda}^{-1}$
by considering the contribution to
$\gg A_{\Lambda}^{-1}$
by considering the contribution to
![]() $A_{\Lambda}$
by scalar multiples of the shortest vector. Therefore
$A_{\Lambda}$
by scalar multiples of the shortest vector. Therefore
![]() $\xi$
is a multiple of
$\xi$
is a multiple of
![]() $\widetilde{\xi}$
which is primitive, we have
$\widetilde{\xi}$
which is primitive, we have
![]() $\lVert\xi\rVert_2/\lVert\widetilde{\xi}\rVert_2\ll (\sqrt{d} + \sqrt{\log A_{\Lambda}})A_{\Lambda}$
, and therefore q can be replaced by
$\lVert\xi\rVert_2/\lVert\widetilde{\xi}\rVert_2\ll (\sqrt{d} + \sqrt{\log A_{\Lambda}})A_{\Lambda}$
, and therefore q can be replaced by
![]() $q' = q\lVert\xi\rVert_2/\lVert\widetilde{\xi}\rVert_2 \ll (\sqrt{d} + \sqrt{\log A_{\Lambda}})A_{\Lambda}\cdot A_{\Lambda}^{C}\ll d\cdot A_{\Lambda}^{C+1}.$
This gives the desired result.
$q' = q\lVert\xi\rVert_2/\lVert\widetilde{\xi}\rVert_2 \ll (\sqrt{d} + \sqrt{\log A_{\Lambda}})A_{\Lambda}\cdot A_{\Lambda}^{C}\ll d\cdot A_{\Lambda}^{C+1}.$
This gives the desired result.
Let
![]() $M = 4(\sqrt{d} + \sqrt{\log A_{\Lambda}})$
and note that
$M = 4(\sqrt{d} + \sqrt{\log A_{\Lambda}})$
and note that
 \begin{align*}1/2&\le |F_{\Lambda,\alpha}(N) - 1| = \bigg|\sum_{\xi\in \Lambda^{\ast}\setminus\{0\}}e^{-\pi \lVert\xi\rVert_2^2}\mathbb{E}_{|n|\le N}e(n^k\xi\cdot \alpha)\bigg|\\&\le \sum_{\substack{\xi\in \Lambda^{\ast}\\ \lVert\xi\rVert_2\ge M}}e^{-\pi \lVert\xi\rVert_2^2} + \bigg(\sup_{\substack{\xi\in \Lambda^{\ast}\\ \lVert\xi\rVert_2\le M}}\Big|\mathbb{E}_{|n|\le N}e(n^k\xi\cdot \alpha)\Big|\bigg)\cdot \sum_{\xi\in \Lambda^{\ast}}e^{-\pi \lVert\xi\rVert_2^2}\\&\le e^{-\pi M^2/2}\sum_{\xi\in \Lambda^{\ast}}e^{-\pi \lVert\xi\rVert_2^2/2} + A_{\Lambda}\sup_{\substack{\xi\in \Lambda^{\ast}\\ \lVert\xi\rVert_2\le M}}\Big|\mathbb{E}_{|n|\le N}e(n^k\xi\cdot \alpha)\Big|\\&= e^{-\pi M^2/2}2^{d/2}\det(\Lambda)\sum_{m\in \Lambda}e^{-2\pi \lVert m\rVert_2^2} + A_{\Lambda}\sup_{\substack{\xi\in \Lambda^{\ast}\\ \lVert\xi\rVert_2\le M}}\Big|\mathbb{E}_{|n|\le N}e(n^k\xi\cdot \alpha)\Big|\\&\le 1/4 + A_{\Lambda}\sup_{\substack{\xi\in \Lambda^{\ast}\\ \lVert\xi\rVert_2\le M}}\Big|\mathbb{E}_{|n|\le N}e(n^k\xi\cdot \alpha)\Big|,\end{align*}
\begin{align*}1/2&\le |F_{\Lambda,\alpha}(N) - 1| = \bigg|\sum_{\xi\in \Lambda^{\ast}\setminus\{0\}}e^{-\pi \lVert\xi\rVert_2^2}\mathbb{E}_{|n|\le N}e(n^k\xi\cdot \alpha)\bigg|\\&\le \sum_{\substack{\xi\in \Lambda^{\ast}\\ \lVert\xi\rVert_2\ge M}}e^{-\pi \lVert\xi\rVert_2^2} + \bigg(\sup_{\substack{\xi\in \Lambda^{\ast}\\ \lVert\xi\rVert_2\le M}}\Big|\mathbb{E}_{|n|\le N}e(n^k\xi\cdot \alpha)\Big|\bigg)\cdot \sum_{\xi\in \Lambda^{\ast}}e^{-\pi \lVert\xi\rVert_2^2}\\&\le e^{-\pi M^2/2}\sum_{\xi\in \Lambda^{\ast}}e^{-\pi \lVert\xi\rVert_2^2/2} + A_{\Lambda}\sup_{\substack{\xi\in \Lambda^{\ast}\\ \lVert\xi\rVert_2\le M}}\Big|\mathbb{E}_{|n|\le N}e(n^k\xi\cdot \alpha)\Big|\\&= e^{-\pi M^2/2}2^{d/2}\det(\Lambda)\sum_{m\in \Lambda}e^{-2\pi \lVert m\rVert_2^2} + A_{\Lambda}\sup_{\substack{\xi\in \Lambda^{\ast}\\ \lVert\xi\rVert_2\le M}}\Big|\mathbb{E}_{|n|\le N}e(n^k\xi\cdot \alpha)\Big|\\&\le 1/4 + A_{\Lambda}\sup_{\substack{\xi\in \Lambda^{\ast}\\ \lVert\xi\rVert_2\le M}}\Big|\mathbb{E}_{|n|\le N}e(n^k\xi\cdot \alpha)\Big|,\end{align*}
where the equality follows from Poisson summation. We therefore have that
and the result follows from Proposition B·2 as desired.
The following appears as [ Reference Green and Tao13 , lemma A·7].
Lemma B·5. Let
![]() $\Lambda'\subseteq\mathbb{R}^{d-1}$
and
$\Lambda'\subseteq\mathbb{R}^{d-1}$
and
![]() $\Lambda\subseteq\mathbb{R}^d$
be full-rank lattices with
$\Lambda\subseteq\mathbb{R}^d$
be full-rank lattices with
![]() $\Lambda'\subseteq \Lambda$
, embedding
$\Lambda'\subseteq \Lambda$
, embedding
![]() $\mathbb{R}^{d-1}$
in
$\mathbb{R}^{d-1}$
in
![]() $\mathbb{R}^d$
by putting 0 in the final coordinate. Suppose that
$\mathbb{R}^d$
by putting 0 in the final coordinate. Suppose that
![]() $\alpha\in\mathbb{R}^d$
and
$\alpha\in\mathbb{R}^d$
and
![]() $\alpha'\in\mathbb{R}^{d-1}$
satisfy
$\alpha'\in\mathbb{R}^{d-1}$
satisfy
![]() $\alpha-\alpha'\in \Lambda$
. Then
$\alpha-\alpha'\in \Lambda$
. Then
We now combine Lemma B·4 and Lemma B·5 exactly as in [ Reference Green and Tao13 , proposition A·8].
Lemma B·6. There exists
![]() $C = C(k) \gt 0$
such that the following holds. Suppose
$C = C(k) \gt 0$
such that the following holds. Suppose
![]() $\alpha\in \mathbb{R}^d$
and
$\alpha\in \mathbb{R}^d$
and
![]() $\Lambda\subset \mathbb{R}^d$
is full rank. If
$\Lambda\subset \mathbb{R}^d$
is full rank. If
![]() $N \gt (dA_{\Lambda})^C$
and
$N \gt (dA_{\Lambda})^C$
and
![]() $F_{\Lambda,\alpha}(N)\le 1/2$
, then there exist
$F_{\Lambda,\alpha}(N)\le 1/2$
, then there exist
![]() $\Lambda'\subseteq \mathbb{R}^{d-1}$
,
$\Lambda'\subseteq \mathbb{R}^{d-1}$
,
![]() $\alpha'\in \mathbb{R}^{d-1}$
, and
$\alpha'\in \mathbb{R}^{d-1}$
, and
![]() $N'\gg N(dA_{\Lambda})^{-C}$
such that
$N'\gg N(dA_{\Lambda})^{-C}$
such that
 \begin{align*}A_{\Lambda'} &\ll (\sqrt{d} + \sqrt{\log A_{\Lambda}})A_{\Lambda},\\F_{\Lambda,\alpha}(N)&\ge(dA_{\Lambda})^{-C}F_{\Lambda',\alpha'}(N^{\ast}).\end{align*}
\begin{align*}A_{\Lambda'} &\ll (\sqrt{d} + \sqrt{\log A_{\Lambda}})A_{\Lambda},\\F_{\Lambda,\alpha}(N)&\ge(dA_{\Lambda})^{-C}F_{\Lambda',\alpha'}(N^{\ast}).\end{align*}
Proof. By Lemma B·4 we have that there exist primitive
![]() $\xi\in \Lambda^{\ast}\setminus\{0\}$
and
$\xi\in \Lambda^{\ast}\setminus\{0\}$
and
![]() $q\ll dA_{\Lambda}^{C}$
such that
$q\ll dA_{\Lambda}^{C}$
such that
By applying a rotation to both
![]() $\alpha$
and
$\alpha$
and
![]() $\Lambda$
, we may assume that
$\Lambda$
, we may assume that
![]() $\xi = \xi_de_d$
. Note that
$\xi = \xi_de_d$
. Note that
![]() $|\xi_d|\gg A_{\Lambda}^{-1}$
and
$|\xi_d|\gg A_{\Lambda}^{-1}$
and
![]() $\lVert\xi\cdot q^k\alpha\rVert_{\mathbb{R}/\mathbb{Z}}\ll d A_{\Lambda}^{O(1)}N^{-k}$
. Thus there exists
$\lVert\xi\cdot q^k\alpha\rVert_{\mathbb{R}/\mathbb{Z}}\ll d A_{\Lambda}^{O(1)}N^{-k}$
. Thus there exists
![]() $\beta\in \mathbb{R}^d$
such that
$\beta\in \mathbb{R}^d$
such that
![]() $\beta\cdot \xi \in \mathbb{Z}$
and
$\beta\cdot \xi \in \mathbb{Z}$
and
We take
![]() $N_{\ast} \gg (dA_{\Lambda})^{-O(1)}N$
such that
$N_{\ast} \gg (dA_{\Lambda})^{-O(1)}N$
such that
![]() $\lVert\beta-q^k\alpha\rVert_{2}\le N_{\ast}^{-k}/d$
. We have that
$\lVert\beta-q^k\alpha\rVert_{2}\le N_{\ast}^{-k}/d$
. We have that
 \begin{align*}F_{\Lambda,\alpha}(N)&\gg (dA_{\Lambda})^{-O(1)}F_{\Lambda,\alpha}(N^{\ast})\gg (dA_{\Lambda})^{-O(1)}F_{\Lambda,q^k\alpha}(N^{\ast}/q)\\&\gg (dA_{\Lambda})^{-O(1)}F_{(1+1/d)\Lambda,(1+1/d)\beta}(N^{\ast}/q),\end{align*}
\begin{align*}F_{\Lambda,\alpha}(N)&\gg (dA_{\Lambda})^{-O(1)}F_{\Lambda,\alpha}(N^{\ast})\gg (dA_{\Lambda})^{-O(1)}F_{\Lambda,q^k\alpha}(N^{\ast}/q)\\&\gg (dA_{\Lambda})^{-O(1)}F_{(1+1/d)\Lambda,(1+1/d)\beta}(N^{\ast}/q),\end{align*}
where we have applied the first, second, and then third item of Lemma B·3. Let
![]() $\pi\colon(x_1,\ldots,x_d)\to(x_1,\ldots,x_{d-1})$
and take
$\pi\colon(x_1,\ldots,x_d)\to(x_1,\ldots,x_{d-1})$
and take
![]() $\alpha' = (1+1/d)\pi(\beta)$
,
$\alpha' = (1+1/d)\pi(\beta)$
,
![]() $\Lambda' = \pi((1+1/d)\Lambda)$
, and
$\Lambda' = \pi((1+1/d)\Lambda)$
, and
![]() $N' = N^{\ast}/q$
. (That
$N' = N^{\ast}/q$
. (That
![]() $\Lambda'$
is a lattice uses that
$\Lambda'$
is a lattice uses that
![]() $\xi$
is primitive.) Finally by Lemma B·5,
$\xi$
is primitive.) Finally by Lemma B·5,
and using the lower bound on
![]() $|\xi_d|$
we have the desired lower bound on
$|\xi_d|$
we have the desired lower bound on
![]() $F_{\Lambda,\alpha}(N)$
. For the upper bound of
$F_{\Lambda,\alpha}(N)$
. For the upper bound of
![]() $A_{\Lambda'}$
, by positivity of the exponential function we have
$A_{\Lambda'}$
, by positivity of the exponential function we have
and therefore
as desired.
Iterating Lemma >B·6 exactly as is done in [ Reference Green and Tao13 , proposition A·9] (see arXiv version for a corrected statement) yields the following.
Proposition B·7. There exists
![]() $C = C(k) \gt 0$
such that the following holds. Let
$C = C(k) \gt 0$
such that the following holds. Let
![]() $\Lambda\subseteq \mathbb{R}^d$
be a lattice of full rank with
$\Lambda\subseteq \mathbb{R}^d$
be a lattice of full rank with
![]() $\det(\Lambda)\ge 1$
. Then for any integer N we have
$\det(\Lambda)\ge 1$
. Then for any integer N we have
We now prove Proposition 3·7; our deduction once again is identical to [ Reference Green and Tao13 , proposition A·2].
Proof of Proposition 3·7. Let R be a quantity to be chosen later;
![]() $R\gg d^3$
throughout. Let
$R\gg d^3$
throughout. Let
![]() $\Lambda \;:\!=\; R\mathbb{Z}^d$
and
$\Lambda \;:\!=\; R\mathbb{Z}^d$
and
![]() $A_{\Lambda} = R^d(\sum_{m\in R\mathbb{Z}}e^{-\pi m^2})^d\le 2^{O(d)}R^d$
. This along with Proposition B·7 implies that
$A_{\Lambda} = R^d(\sum_{m\in R\mathbb{Z}}e^{-\pi m^2})^d\le 2^{O(d)}R^d$
. This along with Proposition B·7 implies that
or
For
![]() $N\gg (2R)^{\Omega(d^2)}$
, there is
$N\gg (2R)^{\Omega(d^2)}$
, there is
![]() $n\in \{1,\ldots N\}$
such that
$n\in \{1,\ldots N\}$
such that
If
![]() $\lVert n^k\alpha - m\rVert_2\ge \sqrt{R}$
for all
$\lVert n^k\alpha - m\rVert_2\ge \sqrt{R}$
for all
![]() $m\in R\mathbb{Z}^d$
, we have
$m\in R\mathbb{Z}^d$
, we have
 \begin{align*}\sum_{m\in R\mathbb{Z}^d}e^{-\pi\lVert n^k\alpha - m\rVert_2^2}&\le e^{-\pi R/2}\sum_{m\in R\mathbb{Z}^d}e^{-\pi\lVert n^k\alpha - m\rVert_2^2/2}\\&= e^{-\pi R/2} \frac{2^{d/2}}{\det(\Lambda)}\sum_{\xi\in \Lambda^{\ast}}e^{-2\pi \lVert\xi\rVert_2^2}\exp\!(\xi\cdot n^k\alpha)\\&\le e^{-\pi R/2} \frac{2^{d/2}A_{\Lambda}}{\det(\Lambda)} \ll e^{-\pi R/2} 2^{O(d)}.\end{align*}
\begin{align*}\sum_{m\in R\mathbb{Z}^d}e^{-\pi\lVert n^k\alpha - m\rVert_2^2}&\le e^{-\pi R/2}\sum_{m\in R\mathbb{Z}^d}e^{-\pi\lVert n^k\alpha - m\rVert_2^2/2}\\&= e^{-\pi R/2} \frac{2^{d/2}}{\det(\Lambda)}\sum_{\xi\in \Lambda^{\ast}}e^{-2\pi \lVert\xi\rVert_2^2}\exp\!(\xi\cdot n^k\alpha)\\&\le e^{-\pi R/2} \frac{2^{d/2}A_{\Lambda}}{\det(\Lambda)} \ll e^{-\pi R/2} 2^{O(d)}.\end{align*}
This is a contradiction; thus if
![]() $N\ge (2R)^{\Omega(d^2)}$
and
$N\ge (2R)^{\Omega(d^2)}$
and
![]() $R\gg d^3$
then there exists
$R\gg d^3$
then there exists
![]() $1\le n\le N$
such that
$1\le n\le N$
such that
for all
![]() $j=1,\ldots, d$
. The result follows upon taking
$j=1,\ldots, d$
. The result follows upon taking
![]() $R = N^{c/d^2}$
for an appropriately small constant c (if N is small enough that
$R = N^{c/d^2}$
for an appropriately small constant c (if N is small enough that
![]() $R\gg d^3$
fails to hold, the result is trivial).
$R\gg d^3$
fails to hold, the result is trivial).
Appendix C. Constructing an periodic nilsequence with integral structure constants
For technical reasons, it will be advantageous to construct nilsequences where the underlying nilmanifold has structure constants which are integral (and in fact divisible by a sufficient fixed integer). This follows via a straightforward lifting procedure where one replaces the underlying Mal’cev basis
![]() $\{e_1,\ldots,e_{\dim(G)}\}$
for
$\{e_1,\ldots,e_{\dim(G)}\}$
for
![]() $\Gamma$
with
$\Gamma$
with
![]() $\{e_1^{L},\ldots,e_{\dim(G)}^{L}\}$
for a sufficiently large constant L. This is primarily to avoid needing various fractional part identities in the proof of Proposition 2·3.
$\{e_1^{L},\ldots,e_{\dim(G)}^{L}\}$
for a sufficiently large constant L. This is primarily to avoid needing various fractional part identities in the proof of Proposition 2·3.
Lemma C·1. Fix an integer
![]() $K\ge 1$
. Suppose we are given a degree s nilmanifold
$K\ge 1$
. Suppose we are given a degree s nilmanifold
![]() $G/\Gamma$
with dimension d and complexity M and
$G/\Gamma$
with dimension d and complexity M and
![]() $F\colon G/\Gamma\to \mathbb{C}$
with Lipschitz norm bounded by L (with respect to the metric
$F\colon G/\Gamma\to \mathbb{C}$
with Lipschitz norm bounded by L (with respect to the metric
![]() $d_{G/\Gamma}$
).
$d_{G/\Gamma}$
).
There exist
![]() $\widetilde{\Gamma},\widetilde{F}$
such that
$\widetilde{\Gamma},\widetilde{F}$
such that
![]() $\widetilde{F}\colon G/\widetilde{\Gamma}\to\mathbb{C}$
such that for any
$\widetilde{F}\colon G/\widetilde{\Gamma}\to\mathbb{C}$
such that for any
![]() $g\in G$
we have
$g\in G$
we have
Furthermore we have that
![]() $\widetilde{\Gamma}$
has a Mal’cev basis
$\widetilde{\Gamma}$
has a Mal’cev basis
![]() $\widetilde{X}$
with all Lie bracket structure constants (the values
$\widetilde{X}$
with all Lie bracket structure constants (the values
![]() $c_{ijk}$
in Definition A·1) being integral and divisible by K, that
$c_{ijk}$
in Definition A·1) being integral and divisible by K, that
![]() $G/\widetilde{\Gamma}$
(with
$G/\widetilde{\Gamma}$
(with
![]() $\widetilde{X}$
) has complexity bounded by
$\widetilde{X}$
) has complexity bounded by
![]() $O_s(K)\cdot\exp\!(O(M))$
, and that F has Lipschitz norm bounded by
$O_s(K)\cdot\exp\!(O(M))$
, and that F has Lipschitz norm bounded by
![]() $L\cdot (K\cdot \exp\!(O(M)))^{O_{s}(d^{O_s(1)})}$
.
$L\cdot (K\cdot \exp\!(O(M)))^{O_{s}(d^{O_s(1)})}$
.
Proof. Let
![]() $\mathcal{X} = \{X_1,\ldots,X_d\}$
denote the Mal’cev basis for the Lie algebra
$\mathcal{X} = \{X_1,\ldots,X_d\}$
denote the Mal’cev basis for the Lie algebra
![]() $\mathfrak{g}$
implicit in the complexity bound given for
$\mathfrak{g}$
implicit in the complexity bound given for
![]() $G/\Gamma$
. In order for
$G/\Gamma$
. In order for
![]() $\mathcal{X}$
to be a Mal’cev basis we have:
$\mathcal{X}$
to be a Mal’cev basis we have:
-
(i) for each
 $j = 0,\ldots,d$
, the subspace
$j = 0,\ldots,d$
, the subspace
 $\mathfrak{h}_j \;:\!=\; \operatorname{span}(X_{j+1},\ldots, X_d)$
is a Lie algebra ideal in
$\mathfrak{h}_j \;:\!=\; \operatorname{span}(X_{j+1},\ldots, X_d)$
is a Lie algebra ideal in
 $\mathfrak{g}$
, and hence
$\mathfrak{g}$
, and hence
 $H_j \;:\!=\; \exp\!(\mathfrak{h}_j)$
is a normal Lie subgroup of G;
$H_j \;:\!=\; \exp\!(\mathfrak{h}_j)$
is a normal Lie subgroup of G; -
(ii) if
 $d_i = \dim(G_i)$
then
$d_i = \dim(G_i)$
then
 $G_i = H_{d-d_i}$
;
$G_i = H_{d-d_i}$
; -
(iii) each
 $g\in G$
may be written uniquely as
$g\in G$
may be written uniquely as
 $\exp\!(t_1X_1)\cdots\exp\!(t_mX_m)$
for
$\exp\!(t_1X_1)\cdots\exp\!(t_mX_m)$
for
 $t_i\in \mathbb{R}$
;
$t_i\in \mathbb{R}$
; -
(iv)
 $\Gamma$
are exactly the elements which can be written in the form
$\Gamma$
are exactly the elements which can be written in the form
 $\exp\!(t_1X_1)\cdots\exp\!(t_mX_m)$
with
$\exp\!(t_1X_1)\cdots\exp\!(t_mX_m)$
with
 $t_i\in \mathbb{Z}$
(and is a discrete cocompact subgroup).
$t_i\in \mathbb{Z}$
(and is a discrete cocompact subgroup).
We also require that the Lie algebra relations are appropriately filtered, corresponding to the containments
![]() $[G_i,G_j]\subseteq G_{i+j}$
.
$[G_i,G_j]\subseteq G_{i+j}$
.
We take
![]() $\widetilde{\mathcal{X}} = \{R\cdot X_1,\ldots,R\cdot X_d\} =: \{\widetilde{X_1},\ldots,\widetilde{X_d}\}$
for a large positive integer R to be chosen later. We take
$\widetilde{\mathcal{X}} = \{R\cdot X_1,\ldots,R\cdot X_d\} =: \{\widetilde{X_1},\ldots,\widetilde{X_d}\}$
for a large positive integer R to be chosen later. We take
![]() $\widetilde{\Gamma} = \langle \exp\!(RX_i) \rangle$
and claim that
$\widetilde{\Gamma} = \langle \exp\!(RX_i) \rangle$
and claim that
![]() $\widetilde{\mathcal{X}}$
is a valid Mal’cev basis for
$\widetilde{\mathcal{X}}$
is a valid Mal’cev basis for
![]() $G,\widetilde{\Gamma}$
. All conditions for verifying a Mal’cev basis are trivial for us except for the fourth bullet point. The key point is verifying that every element of the subgroup generated by elements
$G,\widetilde{\Gamma}$
. All conditions for verifying a Mal’cev basis are trivial for us except for the fourth bullet point. The key point is verifying that every element of the subgroup generated by elements
![]() $\exp\!(RX_i)$
can be presented in the desired form.
$\exp\!(RX_i)$
can be presented in the desired form.
We take
![]() $R = C_s \cdot \operatorname{lcm}(1,\ldots,M)\cdot K$
for some appropriate positive integer
$R = C_s \cdot \operatorname{lcm}(1,\ldots,M)\cdot K$
for some appropriate positive integer
![]() $C_s$
. Note that
$C_s$
. Note that
The crucial point here is that
![]() $Rc_{ijk}\in C_s\mathbb{Z}$
by construction. Let
$Rc_{ijk}\in C_s\mathbb{Z}$
by construction. Let
![]() $e_i = \exp\!(X_i)$
and suppose we have a word in
$e_i = \exp\!(X_i)$
and suppose we have a word in
![]() $\widetilde{\Gamma}$
given by
$\widetilde{\Gamma}$
given by
where each
![]() $\pm$
denotes an appropriate sign. Note
$\pm$
denotes an appropriate sign. Note
![]() $e_i^R=\exp\!(\widetilde{X}_i)$
. We first use the Baker–Campbell–Hausdorff formula to write
$e_i^R=\exp\!(\widetilde{X}_i)$
. We first use the Baker–Campbell–Hausdorff formula to write
 \[w=\exp\bigg(\sum_{j=1}^dw_j\widetilde{X}_j\bigg).\]
\[w=\exp\bigg(\sum_{j=1}^dw_j\widetilde{X}_j\bigg).\]
Note that
![]() $w_j\in\mathbb{Z}$
since the Lie bracket structure constants
$w_j\in\mathbb{Z}$
since the Lie bracket structure constants
![]() $Rc_{ijk}$
are in
$Rc_{ijk}$
are in
![]() $C_s\mathbb{Z}$
, and Baker–Campbell–Hausdorff only goes to finite height due to the bounded step of the nilpotent Lie group. Now we iteratively pull out a single Mal’cev basis element “one at a time”. We have
$C_s\mathbb{Z}$
, and Baker–Campbell–Hausdorff only goes to finite height due to the bounded step of the nilpotent Lie group. Now we iteratively pull out a single Mal’cev basis element “one at a time”. We have
 \[\exp\!(\!-\!w_1\widetilde{X}_1)w=\exp\!(\!-\!w_1\widetilde{X}_1)\exp\bigg(\sum_{j=1}^dw_j\widetilde{X}_j\bigg)=\exp\bigg(\sum_{j=2}^dw_j'\widetilde{X}_j\bigg)\]
\[\exp\!(\!-\!w_1\widetilde{X}_1)w=\exp\!(\!-\!w_1\widetilde{X}_1)\exp\bigg(\sum_{j=1}^dw_j\widetilde{X}_j\bigg)=\exp\bigg(\sum_{j=2}^dw_j'\widetilde{X}_j\bigg)\]
for some
![]() $w_j'\in\mathbb{Z}$
using Baker–Campbell–Hausdorff again. Note that we have eliminated use of
$w_j'\in\mathbb{Z}$
using Baker–Campbell–Hausdorff again. Note that we have eliminated use of
![]() $\widetilde{X}_1$
in the right side (which uses the observation that
$\widetilde{X}_1$
in the right side (which uses the observation that
![]() $c_{ijk}=0$
if
$c_{ijk}=0$
if
![]() $k\le\max(i,j)$
). We iterate this, obtaining
$k\le\max(i,j)$
). We iterate this, obtaining
 \[\bigg(\prod_{j=d}^1\exp\!(\!-\!w_j^\ast\widetilde{X}_j)\bigg)w=\exp\!(0)=\mathrm{id}_G\]
\[\bigg(\prod_{j=d}^1\exp\!(\!-\!w_j^\ast\widetilde{X}_j)\bigg)w=\exp\!(0)=\mathrm{id}_G\]
for appropriate
![]() $w_j^\ast\in\mathbb{Z}$
(note that the product has decreasing indices left-to-right). Solving for w gives the result. This completes the proof that
$w_j^\ast\in\mathbb{Z}$
(note that the product has decreasing indices left-to-right). Solving for w gives the result. This completes the proof that
![]() $\widetilde{\mathcal{X}}$
is a valid Mal’cev basis.
$\widetilde{\mathcal{X}}$
is a valid Mal’cev basis.
Now we define
![]() $\widetilde{F}$
and verify various claims regarding bounds. Note that
$\widetilde{F}$
and verify various claims regarding bounds. Note that
![]() $G/\widetilde{\Gamma}$
clearly has complexity bounded by O(RM) which is as desired. Since
$G/\widetilde{\Gamma}$
clearly has complexity bounded by O(RM) which is as desired. Since
![]() $\widetilde{\Gamma}\subseteq \Gamma$
, we may lift F from
$\widetilde{\Gamma}\subseteq \Gamma$
, we may lift F from
![]() $G/\Gamma$
to
$G/\Gamma$
to
![]() $\widetilde{F}$
on
$\widetilde{F}$
on
![]() $G/\widetilde{\Gamma}$
in the obvious manner, composing with a quotient. It suffices to verify that this does not ruin the Lipschitz norm. Let
$G/\widetilde{\Gamma}$
in the obvious manner, composing with a quotient. It suffices to verify that this does not ruin the Lipschitz norm. Let
![]() $M' = \exp\!(O(M))\cdot O_s(K)$
; we have that the diameter of
$M' = \exp\!(O(M))\cdot O_s(K)$
; we have that the diameter of
![]() $G/\widetilde{\Gamma}$
is bounded by
$G/\widetilde{\Gamma}$
is bounded by
![]() $(M')^{O_s(d^{O_s(1)})}$
(cf. [
Reference Green and Tao11
, lemma A·16] with explicit dimension dependence [
Reference Leng22
, lemma B·8]). Since
$(M')^{O_s(d^{O_s(1)})}$
(cf. [
Reference Green and Tao11
, lemma A·16] with explicit dimension dependence [
Reference Leng22
, lemma B·8]). Since
![]() $\lVert\widetilde{F}\rVert_\infty=\lVert F\rVert_\infty\le\lVert F\rVert_{\mathrm{Lip}}\le L$
, it suffices to consider points which are within
$\lVert\widetilde{F}\rVert_\infty=\lVert F\rVert_\infty\le\lVert F\rVert_{\mathrm{Lip}}\le L$
, it suffices to consider points which are within
![]() $d_{G/\widetilde{\Gamma}}$
distance
$d_{G/\widetilde{\Gamma}}$
distance
![]() $\varepsilon$
when verifying the Lipschitz bound for
$\varepsilon$
when verifying the Lipschitz bound for
![]() $\widetilde{F}$
as long as we are willing to lose a factor of
$\widetilde{F}$
as long as we are willing to lose a factor of
![]() $\varepsilon^{-1}$
.
$\varepsilon^{-1}$
.
Note that
![]() $d_{G,\widetilde{\mathcal{X}}}(x,y)=(1/R)d_{G,\mathcal{X}}(x,y)$
since Mal’cev coordinates of the second kind in
$d_{G,\widetilde{\mathcal{X}}}(x,y)=(1/R)d_{G,\mathcal{X}}(x,y)$
since Mal’cev coordinates of the second kind in
![]() $\mathcal{X},\widetilde{\mathcal{X}}$
differ by a factor of R. Now consider
$\mathcal{X},\widetilde{\mathcal{X}}$
differ by a factor of R. Now consider
![]() $x,y\in G/\widetilde{\Gamma}$
such that
$x,y\in G/\widetilde{\Gamma}$
such that
![]() $d_{G/\widetilde{\Gamma}}(x,y)\le(M')^{-O_s(d^{O_s(1)})}$
. There exist representatives of
$d_{G/\widetilde{\Gamma}}(x,y)\le(M')^{-O_s(d^{O_s(1)})}$
. There exist representatives of
![]() $\widetilde{x}$
and
$\widetilde{x}$
and
![]() $\widetilde{y}$
for x and y with respect to
$\widetilde{y}$
for x and y with respect to
![]() $\widetilde{\Gamma}$
such that
$\widetilde{\Gamma}$
such that
Additionally, we claim that since x, y are sufficiently close in
![]() $G/\widetilde{\Gamma}$
, we find that
$G/\widetilde{\Gamma}$
, we find that
The argument is as follows. If this is not true, then there is
![]() $\gamma\in\Gamma\setminus\{0\}$
with
$\gamma\in\Gamma\setminus\{0\}$
with
![]() $d_{G,\mathcal{X}}(\widetilde{x},\widetilde{y}\gamma) \lt d_{G,\mathcal{X}}(\widetilde{x},\widetilde{y})$
. By approximate left-invariance of the metric on G ([
Reference Green and Tao11
, lemma A·5] with explicit dimension dependence [
Reference Leng22
, lemma B·4]) we see
$d_{G,\mathcal{X}}(\widetilde{x},\widetilde{y}\gamma) \lt d_{G,\mathcal{X}}(\widetilde{x},\widetilde{y})$
. By approximate left-invariance of the metric on G ([
Reference Green and Tao11
, lemma A·5] with explicit dimension dependence [
Reference Leng22
, lemma B·4]) we see
Additionally,
The triangle inequality yields
Now, the metric is comparable to the
![]() $L^\infty$
distance in second kind Mal’cev coordinates up to a factor of
$L^\infty$
distance in second kind Mal’cev coordinates up to a factor of
![]() $(M')^{O_s(d^{O_s(1)})}$
([
Reference Green and Tao11
, lemma A·4] with explicit dimension dependence [
Reference Leng22
, lemma B·3]) as long as
$(M')^{O_s(d^{O_s(1)})}$
([
Reference Green and Tao11
, lemma A·4] with explicit dimension dependence [
Reference Leng22
, lemma B·3]) as long as
![]() $\varepsilon$
is sufficiently small here, so we find
$\varepsilon$
is sufficiently small here, so we find
This as a contradiction as long as we take sufficiently small
![]() $\varepsilon$
(which will be admissible in the bounds we need). Finally,
$\varepsilon$
(which will be admissible in the bounds we need). Finally,
 \begin{align*}|\widetilde{F}(x\widetilde{\Gamma})-\widetilde{F}(y\widetilde{\Gamma})|&=|F(\widetilde{x}\Gamma)-F(\widetilde{y}\Gamma)|\le Ld_{G/\Gamma}(\widetilde{x},\widetilde{y})=Ld_{G,\mathcal{X}}(\widetilde{x},\widetilde{y})=LRd_{G,\widetilde{\mathcal{X}}}(\widetilde{x},\widetilde{y})\\[5pt] &=LRd_{G/\widetilde{\Gamma}}(x,y)\end{align*}
\begin{align*}|\widetilde{F}(x\widetilde{\Gamma})-\widetilde{F}(y\widetilde{\Gamma})|&=|F(\widetilde{x}\Gamma)-F(\widetilde{y}\Gamma)|\le Ld_{G/\Gamma}(\widetilde{x},\widetilde{y})=Ld_{G,\mathcal{X}}(\widetilde{x},\widetilde{y})=LRd_{G,\widetilde{\mathcal{X}}}(\widetilde{x},\widetilde{y})\\[5pt] &=LRd_{G/\widetilde{\Gamma}}(x,y)\end{align*}
and we are done.
Having constructed a nilsequence with integral Lie bracket structure constants, it will also prove useful to construct a nilsequence which is additionally periodic. For this purpose, we quantify a construction of Manners [ Reference Manners24 ] which demonstrates that one may lift a nilsequence along a subset of the support. We first give a quantified version of [ Reference Manners24 , theorem 1·5].
Proposition C·2. There is an integer
![]() $C_s\ge 1$
so that the following holds. Fix an integer
$C_s\ge 1$
so that the following holds. Fix an integer
![]() $K\ge 1$
. Suppose we have a degree s nilmanifold
$K\ge 1$
. Suppose we have a degree s nilmanifold
![]() $G/\Gamma$
with complexity M and
$G/\Gamma$
with complexity M and
![]() $F\colon G/\Gamma\to\mathbb{C}$
with Lipschitz norm L. Furthermore suppose we have a polynomial sequence
$F\colon G/\Gamma\to\mathbb{C}$
with Lipschitz norm L. Furthermore suppose we have a polynomial sequence
![]() $g\colon\mathbb{Z}\to G$
and a smooth function
$g\colon\mathbb{Z}\to G$
and a smooth function
![]() $\phi\colon\mathbb{R}/\mathbb{Z}\to[0,1]$
with
$\phi\colon\mathbb{R}/\mathbb{Z}\to[0,1]$
with
![]() $\operatorname{supp}(\phi)\in [(3K)^{-1},(2K)^{-1}]$
.
$\operatorname{supp}(\phi)\in [(3K)^{-1},(2K)^{-1}]$
.
There exists a degree s nilmanifold
![]() $\widetilde{G}/\widetilde{\Gamma}$
with a polynomial sequence
$\widetilde{G}/\widetilde{\Gamma}$
with a polynomial sequence
![]() $\tilde{g}\colon\mathbb{Z}\to \widetilde{G}$
such that
$\tilde{g}\colon\mathbb{Z}\to \widetilde{G}$
such that
where
![]() $x \;\mathrm{mod}\;N$
is interpreted to lie in
$x \;\mathrm{mod}\;N$
is interpreted to lie in
![]() $\{0,\ldots,N-1\}$
. Furthermore we may assume:
$\{0,\ldots,N-1\}$
. Furthermore we may assume:
-
(i)
 $\widetilde{G}/\widetilde{\Gamma}$
has complexity bounded by
$\widetilde{G}/\widetilde{\Gamma}$
has complexity bounded by
 $O_K(1)^{O_s(1)} + O_s(M)$
and dimension at most
$O_K(1)^{O_s(1)} + O_s(M)$
and dimension at most
 $O_s(d)$
;
$O_s(d)$
; -
(ii)
 $\widetilde{F}$
has Lipschitz norm bounded by
$\widetilde{F}$
has Lipschitz norm bounded by
 $L\cdot O_{\phi,K}(M^{O_s(d^{O_s(1)})})$
;
$L\cdot O_{\phi,K}(M^{O_s(d^{O_s(1)})})$
; -
(iii)
 $\widetilde{g}(n)^{-1}\widetilde{g}(n+N)\in\widetilde{\Gamma}$
for all
$\widetilde{g}(n)^{-1}\widetilde{g}(n+N)\in\widetilde{\Gamma}$
for all
 $n\in\mathbb{Z}$
;
$n\in\mathbb{Z}$
; -
(iv) if all Lie bracket structure constants of
 $G/\Gamma$
are integers divisible by K then the Lie bracket structure constants of
$G/\Gamma$
are integers divisible by K then the Lie bracket structure constants of
 $\widetilde{G}/\widetilde{\Gamma}$
are contained in
$\widetilde{G}/\widetilde{\Gamma}$
are contained in
 $K(C_s)^{-1}\mathbb{Z}$
.
$K(C_s)^{-1}\mathbb{Z}$
.
Given this we deduce a variant of the
![]() $U^4$
-inverse theorem from Theorem 1·3. This argument is essentially a combination of Lemma C·1, Proposition C·2, and the argument of [
Reference Manners24
, theorem 1·4].
$U^4$
-inverse theorem from Theorem 1·3. This argument is essentially a combination of Lemma C·1, Proposition C·2, and the argument of [
Reference Manners24
, theorem 1·4].
Theorem C·3. Suppose we have an integer
![]() $K\ge 1$
. There exists a constant
$K\ge 1$
. There exists a constant
![]() $C=C_K \gt 0$
such that the following holds. Let N be prime, let
$C=C_K \gt 0$
such that the following holds. Let N be prime, let
![]() $\delta \gt 0$
, and suppose that
$\delta \gt 0$
, and suppose that
![]() $f\colon\mathbb{Z}/N\mathbb{Z}\to\mathbb{C}$
is a 1-bounded function with
$f\colon\mathbb{Z}/N\mathbb{Z}\to\mathbb{C}$
is a 1-bounded function with
There exists a degree 3 nilsequence
![]() $F(g(n)\Gamma)$
such that it has dimension bounded by
$F(g(n)\Gamma)$
such that it has dimension bounded by
![]() $(\!\log\!(1/\delta))^{C}$
, complexity bounded by
$(\!\log\!(1/\delta))^{C}$
, complexity bounded by
![]() $O_K(1)$
, such that F is 1-Lipschitz, and such that
$O_K(1)$
, such that F is 1-Lipschitz, and such that
Furthermore, all Lie bracket structure constants of G (the
![]() $c_{ijk}$
in Definition A·1) are integers divisible by K,
$c_{ijk}$
in Definition A·1) are integers divisible by K,
![]() $g(n)g(n+N)^{-1}\in\Gamma$
for all
$g(n)g(n+N)^{-1}\in\Gamma$
for all
![]() $n\in\mathbb{Z}$
, and
$n\in\mathbb{Z}$
, and
![]() $g(0) = \operatorname{id}_G$
.
$g(0) = \operatorname{id}_G$
.
Remark. In all our applications, we will take
![]() $K = 12$
.
$K = 12$
.
We deduce Theorem C·3 from Proposition C·2; this is essentially as in the proof of [ Reference Manners24 , theorem 1·4].
Proof of Theorem C·3. By adjusting constants appropriately, we may assume that N is larger than an absolute constant (and for small N apply the
![]() $U^2$
-inverse theorem noting all Lie bracket structure constants for an abelian nilmanifold are 0).
$U^2$
-inverse theorem noting all Lie bracket structure constants for an abelian nilmanifold are 0).
We take a partition of unity of
![]() $\mathbb{R}/\mathbb{Z}$
denoted
$\mathbb{R}/\mathbb{Z}$
denoted
![]() $\phi_1,\ldots,\phi_{20K}\colon\mathbb{R}/\mathbb{Z}\to\mathbb{R}$
such that
$\phi_1,\ldots,\phi_{20K}\colon\mathbb{R}/\mathbb{Z}\to\mathbb{R}$
such that
![]() $\operatorname{supp}(\phi_j)\subseteq[j/(20K),j/(20 K) + 1/(10K)]\;\mathrm{mod}\;1$
. We abusively denote
$\operatorname{supp}(\phi_j)\subseteq[j/(20K),j/(20 K) + 1/(10K)]\;\mathrm{mod}\;1$
. We abusively denote
![]() $\phi_i\colon\mathbb{Z}/N\mathbb{Z}\to\mathbb{R}$
via
$\phi_i\colon\mathbb{Z}/N\mathbb{Z}\to\mathbb{R}$
via
![]() $\phi_i(n) \;:\!=\; \phi_i(n/N)$
. Recalling that
$\phi_i(n) \;:\!=\; \phi_i(n/N)$
. Recalling that
![]() $\lVert\cdot\rVert_{U^4(\mathbb{Z}/N\mathbb{Z})}$
is a norm, we have
$\lVert\cdot\rVert_{U^4(\mathbb{Z}/N\mathbb{Z})}$
is a norm, we have
 \[\lVert f\rVert_{U^4(\mathbb{Z}/N\mathbb{Z})}\le \sum_{i=1}^{20K}\lVert\phi_i f\rVert_{U^4(\mathbb{Z}/N\mathbb{Z})}.\]
\[\lVert f\rVert_{U^4(\mathbb{Z}/N\mathbb{Z})}\le \sum_{i=1}^{20K}\lVert\phi_i f\rVert_{U^4(\mathbb{Z}/N\mathbb{Z})}.\]
Thus there exists an index k such that
![]() $\lVert\phi_k f\rVert_{U^k(\mathbb{Z}/N\mathbb{Z})}\ge \delta/(20 K)$
. Applying a translation, we may assume that
$\lVert\phi_k f\rVert_{U^k(\mathbb{Z}/N\mathbb{Z})}\ge \delta/(20 K)$
. Applying a translation, we may assume that
![]() $\operatorname{supp}(\phi_k f)$
is contained in
$\operatorname{supp}(\phi_k f)$
is contained in
![]() $[\lceil N/(3K)\rceil,\lfloor N/(2K)\rfloor] \;\mathrm{mod}\;N$
.
$[\lceil N/(3K)\rceil,\lfloor N/(2K)\rfloor] \;\mathrm{mod}\;N$
.
Applying Theorem 1·3, we have that there exists degree 3 nilsequence
![]() $F_1(g_1(n)\Gamma_1)$
on
$F_1(g_1(n)\Gamma_1)$
on
![]() $G/\Gamma_1$
with complexity O(1), dimension
$G/\Gamma_1$
with complexity O(1), dimension
![]() $(\!\log\!(1/\delta))^{O(1)}$
, and Lipschitz constant 1 such that
$(\!\log\!(1/\delta))^{O(1)}$
, and Lipschitz constant 1 such that
By Lemma C·1, we may construct
![]() $\Gamma_2,F_2$
with Lie bracket structure constants for
$\Gamma_2,F_2$
with Lie bracket structure constants for
![]() $G/\Gamma_2$
being integers divisible by
$G/\Gamma_2$
being integers divisible by
![]() $K\cdot C_s$
(where
$K\cdot C_s$
(where
![]() $s=3$
) such that
$s=3$
) such that
Furthermore
![]() $G/\Gamma_2$
has complexity bounded by O(K) and
$G/\Gamma_2$
has complexity bounded by O(K) and
![]() $F_2$
has Lipschitz norm bounded by
$F_2$
has Lipschitz norm bounded by
![]() $(2K)^{O(d^{O(1)})}$
. Next, we may write
$(2K)^{O(d^{O(1)})}$
. Next, we may write
and apply Proposition C·2 to
![]() $\phi(x/N) F_2(g_2(x)\Gamma_2)$
. In particular, we obtain
$\phi(x/N) F_2(g_2(x)\Gamma_2)$
. In particular, we obtain
![]() $F_3$
,
$F_3$
,
![]() $G_3$
,
$G_3$
,
![]() $\Gamma_3$
, and
$\Gamma_3$
, and
![]() $g_3(n)$
such that
$g_3(n)$
such that
with
![]() $F_3$
having Lipschitz norm
$F_3$
having Lipschitz norm
![]() $(O_K(1))^{O(d^{O(1)})}$
,
$(O_K(1))^{O(d^{O(1)})}$
,
![]() $G_3/\Gamma_3$
having complexity
$G_3/\Gamma_3$
having complexity
![]() $O_K(1)$
,
$O_K(1)$
,
![]() $g_3(n)$
being N-periodic, and all Lie structure constants divisible by K.
$g_3(n)$
being N-periodic, and all Lie structure constants divisible by K.
Note that we do not necessarily have
![]() $g_3(0) \neq \operatorname{id}_{G_3}$
. This may be repaired by defining
$g_3(0) \neq \operatorname{id}_{G_3}$
. This may be repaired by defining
![]() $g(n) = \{g_3(0)\}^{-1}g_3(n)g_3(0)^{-1}\{g_3(0)\}$
where
$g(n) = \{g_3(0)\}^{-1}g_3(n)g_3(0)^{-1}\{g_3(0)\}$
where
![]() $\{g_3(0)\}^{-1}g_3(0) = [g_3(0)]\in \Gamma_3$
and
$\{g_3(0)\}^{-1}g_3(0) = [g_3(0)]\in \Gamma_3$
and
![]() $\{g_3(0)\}$
has Mal’cev coordinates of the second kind bounded by
$\{g_3(0)\}$
has Mal’cev coordinates of the second kind bounded by
![]() $1/2$
. Taking
$1/2$
. Taking
we have
As left-multiplication by bounded elements preserves the metric up to an admissible multiplicative factor ([
Reference Leng22
, lemma B·4]), we find that F has Lipschitz norm
![]() $(O_K(1))^{O(d^{O(1)})}$
. Thus, rescaling F to have Lipschitz norm 1 will keep the correlation sufficiently large. Furthermore as left-multiplying a fixed element and right-multiplying a fixed element in
$(O_K(1))^{O(d^{O(1)})}$
. Thus, rescaling F to have Lipschitz norm 1 will keep the correlation sufficiently large. Furthermore as left-multiplying a fixed element and right-multiplying a fixed element in
![]() $\Gamma_3$
does not change whether our polynomial sequence is N-periodic on
$\Gamma_3$
does not change whether our polynomial sequence is N-periodic on
![]() $G_3/\Gamma_3$
this completes the proof.
$G_3/\Gamma_3$
this completes the proof.
We now prove Proposition C·2. We use the construction of Manners [ Reference Manners24 , theorem 1·5]; we modify the construction slightly to match the definition of filtration used in this paper.
Proof of Proposition C·2. Step 1. Setup and constructing the proposed Mal’cev basis. We consider the given degree s nilpotent Lie group G with filtration
Let
![]() $\mathfrak{g}_j=\log_G(G_j)$
.
$\mathfrak{g}_j=\log_G(G_j)$
.
For
![]() $i\ge 0$
, let
$i\ge 0$
, let
![]() $G^{+i}$
denote the prefiltration
$G^{+i}$
denote the prefiltration
![]() $G_i\geqslant G_{i+1}\geqslant G_{i+2}\geqslant\cdots \geqslant G_s\geqslant\operatorname{Id}_G$
. Let
$G_i\geqslant G_{i+1}\geqslant G_{i+2}\geqslant\cdots \geqslant G_s\geqslant\operatorname{Id}_G$
. Let
![]() $H_i = \operatorname{poly}(\mathbb{Z},G^{+i})$
, where we define polynomial sequences with respect to prefiltrations as in [
Reference Green, Tao and Ziegler15
, definition B·1] with the prefiltration
$H_i = \operatorname{poly}(\mathbb{Z},G^{+i})$
, where we define polynomial sequences with respect to prefiltrations as in [
Reference Green, Tao and Ziegler15
, definition B·1] with the prefiltration
![]() $\mathbb{Z}\geqslant\mathbb{Z}\geqslant\{0\}\geqslant\cdots$
on the domain
$\mathbb{Z}\geqslant\mathbb{Z}\geqslant\{0\}\geqslant\cdots$
on the domain
![]() $\mathbb{Z}$
(see also [
Reference Green and Tao11
, p. 28], which includes the formal definition of prefiltrations).
$\mathbb{Z}$
(see also [
Reference Green and Tao11
, p. 28], which includes the formal definition of prefiltrations).
By the Filtered Lazard–Leibman theorem of Green, Tao and Ziegler [
Reference Green, Tao and Ziegler15
, proposition B·6],
![]() $H_i$
are not only groups but also can be given the prefiltration
$H_i$
are not only groups but also can be given the prefiltration
This implies that one has the genuine filtration
We now define the semidirect product
![]() $H_i\rtimes\mathbb{R}$
by defining a group operation
$H_i\rtimes\mathbb{R}$
by defining a group operation
![]() $\ast$
via
$\ast$
via
Note that this is slightly different than that given in the work of Manners [
Reference Manners24
], since we take right-quotients by the cocompact subgroup, and in fact this is rather the opposite group of the semidirect product of the opposite groups (but we suppress such notational dependence). The semidirect product in question is embedding
![]() $t\in\mathbb{R}$
as the “shift by t” automorphism. Additionally, we abusively identify
$t\in\mathbb{R}$
as the “shift by t” automorphism. Additionally, we abusively identify
![]() $g\in\operatorname{poly}(\mathbb{Z},G^{+i})$
with a function
$g\in\operatorname{poly}(\mathbb{Z},G^{+i})$
with a function
![]() $\mathbb{R}\to G^{+i}$
defined by using Taylor expansion and then allowing the argument to vary over reals instead of integers using the Lie group structure; this extension is unique due to a generalisation of the identity theorem.
$\mathbb{R}\to G^{+i}$
defined by using Taylor expansion and then allowing the argument to vary over reals instead of integers using the Lie group structure; this extension is unique due to a generalisation of the identity theorem.
One can easily prove that
is a prefiltration; this follows immediately from the proof given in [
Reference Host and Kra17
, proposition 14]. (The only nontrivial aspect involves the
![]() $\rtimes\mathbb{R}$
component, and it is not too hard to show that it suffices to check relevant properties at the level of the generators
$\rtimes\mathbb{R}$
component, and it is not too hard to show that it suffices to check relevant properties at the level of the generators
![]() $(\operatorname{id}_{H_0},t)$
since we have the above prefiltration on
$(\operatorname{id}_{H_0},t)$
since we have the above prefiltration on
![]() $H_0$
.)
$H_0$
.)
Let
![]() $X_1,\ldots,X_d$
denote the Mal’cev basis on the Lie algebra associated to G (which is adapted to the s-step filtration given at the beginning). We construct the desired Mal’cev basis for
$X_1,\ldots,X_d$
denote the Mal’cev basis on the Lie algebra associated to G (which is adapted to the s-step filtration given at the beginning). We construct the desired Mal’cev basis for
![]() $H_0\rtimes\mathbb{R}$
as follows:
$H_0\rtimes\mathbb{R}$
as follows:
-
(i) Let
 $Z = (0,K)$
;
$Z = (0,K)$
; -
(ii) let
 $Y_{i, k} = (n \mapsto \binom{n}{k}X_i, 0)$
; if
$Y_{i, k} = (n \mapsto \binom{n}{k}X_i, 0)$
; if
 $X_i\in \mathfrak{g}_j\setminus \mathfrak{g}_{j+1}$
define the level of
$X_i\in \mathfrak{g}_j\setminus \mathfrak{g}_{j+1}$
define the level of
 $Y_{i,k}$
to be
$Y_{i,k}$
to be
 $j-k$
. We restrict attention to
$j-k$
. We restrict attention to
 $Y_{i,k}$
of nonnegative level and level at most s. (Note that there are no contributions with
$Y_{i,k}$
of nonnegative level and level at most s. (Note that there are no contributions with
 $j=0$
.)
$j=0$
.) -
(iii) we order the Mal’cev basis left-to-right by increasing level; within level we order with increasing k, and then in increasing order of i. Z is inserted as the first element of level 1.
Remark. By Taylor expansion (see [
Reference Green, Tao and Ziegler15
, lemma B·9]) we see that this is a Lie basis of the necessary group, filtered with respect to the desired prefiltration. Note that a priori the Lie algebra of
![]() $\operatorname{poly}(\mathbb{Z},G^{+0})$
is some abstract space, but we can utilise the embedding
$\operatorname{poly}(\mathbb{Z},G^{+0})$
is some abstract space, but we can utilise the embedding
![]() $H_0=\operatorname{poly}(\mathbb{Z},G^{+0})\hookrightarrow G^{\mathbb{Z}}$
and the corresponding representation of Lie algebras to yield the above form of writing elements of the tangent space.
$H_0=\operatorname{poly}(\mathbb{Z},G^{+0})\hookrightarrow G^{\mathbb{Z}}$
and the corresponding representation of Lie algebras to yield the above form of writing elements of the tangent space.
Our goal is now to verify that the discrete cocompact subgroup
![]() $\widetilde{\Gamma} = \operatorname{poly}(\mathbb{Z},\Gamma)\rtimes (K\mathbb{Z})$
is the push-forward of
$\widetilde{\Gamma} = \operatorname{poly}(\mathbb{Z},\Gamma)\rtimes (K\mathbb{Z})$
is the push-forward of
![]() $\mathbb{Z}^{\dim(\widetilde{G})}$
for Mal’cev coordinates of the second kind. This algorithmic proof will also immediately verify the remaining property of the Mal’cev basis (regarding rationality of the Lie bracket structure constants). After this, we will give the necessary nilsequence lifting construction and verify the necessary properties.
$\mathbb{Z}^{\dim(\widetilde{G})}$
for Mal’cev coordinates of the second kind. This algorithmic proof will also immediately verify the remaining property of the Mal’cev basis (regarding rationality of the Lie bracket structure constants). After this, we will give the necessary nilsequence lifting construction and verify the necessary properties.
Step 2. Verifying Mal’cev properties modulo the semidirect product. We first prove that the
![]() $Y_{i,k}$
graded as above form a Mal’cev basis for
$Y_{i,k}$
graded as above form a Mal’cev basis for
with discrete cocompact subgroup
![]() $\Gamma'=\operatorname{poly}(\mathbb{Z},\Gamma)$
. We proceed by induction upwards by step. Note that handling the final step is trivial as the group
$\Gamma'=\operatorname{poly}(\mathbb{Z},\Gamma)$
. We proceed by induction upwards by step. Note that handling the final step is trivial as the group
![]() $H_s$
is abelian.
$H_s$
is abelian.
Assume the inductive hypothesis that
![]() $H_{j+1}\cap\Gamma'$
is the image of the integer lattice in Mal’cev coordinates of the second kind (which necessarily uses only those basis elements of level at least
$H_{j+1}\cap\Gamma'$
is the image of the integer lattice in Mal’cev coordinates of the second kind (which necessarily uses only those basis elements of level at least
![]() $j+1$
). Using Taylor expansion (see [
Reference Green, Tao and Ziegler15
, lemma B·9]), we may write an element
$j+1$
). Using Taylor expansion (see [
Reference Green, Tao and Ziegler15
, lemma B·9]), we may write an element
![]() $H_{j}\cap\Gamma'$
as
$H_{j}\cap\Gamma'$
as
 \begin{equation}n\mapsto \prod_{i=0}^{s-j}g_{i+j}^{\binom{n}{i}},\end{equation}
\begin{equation}n\mapsto \prod_{i=0}^{s-j}g_{i+j}^{\binom{n}{i}},\end{equation}
where
![]() $g_i\in G_{i+j}\cap \Gamma$
. (
$g_i\in G_{i+j}\cap \Gamma$
. (
![]() $g_i\in\Gamma$
easily follows from our polynomial lying in
$g_i\in\Gamma$
easily follows from our polynomial lying in
![]() $\Gamma'=\operatorname{poly}(\mathbb{Z},\Gamma)$
sequence.)
$\Gamma'=\operatorname{poly}(\mathbb{Z},\Gamma)$
sequence.)
Now, for our given value of j, we prove by an induction on
![]() $\ell$
that the set of polynomials of the form
$\ell$
that the set of polynomials of the form
 \[n\mapsto \prod_{i=0}^{s-j}g_{i+j}^{\binom{n}{i}}\]
\[n\mapsto \prod_{i=0}^{s-j}g_{i+j}^{\binom{n}{i}}\]
with
![]() $g_{i+j}\in G_{i+j+1}\cap \Gamma$
for
$g_{i+j}\in G_{i+j+1}\cap \Gamma$
for
![]() $0\le i\le\ell$
and
$0\le i\le\ell$
and
![]() $g_i\in G_{i+j}\cap\Gamma$
for
$g_i\in G_{i+j}\cap\Gamma$
for
![]() $\ell+1\le i\le s-j$
is generated by the level
$\ell+1\le i\le s-j$
is generated by the level
![]() $j+1$
elements and the largest
$j+1$
elements and the largest
![]() $s-j-\ell$
“types” of level j elements of the Mal’cev basis for
$s-j-\ell$
“types” of level j elements of the Mal’cev basis for
![]() $H_0$
. (Here “types” means in the sense of the parameter k we used to define the ordering on the
$H_0$
. (Here “types” means in the sense of the parameter k we used to define the ordering on the
![]() $Y_{i,k}$
above.) The case
$Y_{i,k}$
above.) The case
![]() $\ell = s-j$
is exactly the above inductive assumption regarding
$\ell = s-j$
is exactly the above inductive assumption regarding
![]() $H_{j+1}\cap\Gamma'$
, and the case
$H_{j+1}\cap\Gamma'$
, and the case
![]() $\ell=0$
is exactly what we need to complete the (outer) induction.
$\ell=0$
is exactly what we need to complete the (outer) induction.
We now suppose that this is known for some
![]() $s-j\ge\ell\ge 1$
, and wish to prove the result for
$s-j\ge\ell\ge 1$
, and wish to prove the result for
![]() $\ell-1$
. We may write
$\ell-1$
. We may write
 \[\bigg(n\mapsto \prod_{i=0}^{s-j}g_{i+j}^{\binom{n}{i}}\bigg) = \bigg(n\mapsto \prod_{i=0}^{\ell-1}g_{i+j}^{\binom{n}{i}}\bigg) \bigg(n\mapsto g_{\ell + j}^{\binom{n}{\ell}}\bigg)\bigg(n\mapsto \prod_{i=\ell + 1}^{s-j}g_{i+j}^{\binom{n}{i}}\bigg)=ABC,\]
\[\bigg(n\mapsto \prod_{i=0}^{s-j}g_{i+j}^{\binom{n}{i}}\bigg) = \bigg(n\mapsto \prod_{i=0}^{\ell-1}g_{i+j}^{\binom{n}{i}}\bigg) \bigg(n\mapsto g_{\ell + j}^{\binom{n}{\ell}}\bigg)\bigg(n\mapsto \prod_{i=\ell + 1}^{s-j}g_{i+j}^{\binom{n}{i}}\bigg)=ABC,\]
where A, B, C are defined in the obvious way. Note that
![]() $A\in H_{j+1}\cap\Gamma'$
. We may write
$A\in H_{j+1}\cap\Gamma'$
. We may write
![]() $g_{\ell+j} = \prod_{r}\exp\!(t_rX_r)$
for
$g_{\ell+j} = \prod_{r}\exp\!(t_rX_r)$
for
![]() $t_r\in\mathbb{Z}$
and
$t_r\in\mathbb{Z}$
and
![]() $X_r\in \mathfrak{g}_{\ell+j}$
. Note that
$X_r\in \mathfrak{g}_{\ell+j}$
. Note that
 \[D^{-1}B=\bigg(\prod_{r}\bigg(n\mapsto \exp\!(t_rX_r)^{\binom{n}{\ell}}\bigg)\bigg)^{-1}\bigg(n\mapsto g_{\ell + j}^{\binom{n}{\ell}}\bigg) \in H_j\cap\Gamma',\]
\[D^{-1}B=\bigg(\prod_{r}\bigg(n\mapsto \exp\!(t_rX_r)^{\binom{n}{\ell}}\bigg)\bigg)^{-1}\bigg(n\mapsto g_{\ell + j}^{\binom{n}{\ell}}\bigg) \in H_j\cap\Gamma',\]
where D is defined in the obvious way. The Taylor expansion of the polynomial
![]() $(D^{-1}B)C$
(in a similar form to (C·1)) trivially has its coordinates of index
$(D^{-1}B)C$
(in a similar form to (C·1)) trivially has its coordinates of index
![]() $0,\ldots,\ell-1$
being the identity (plugging in the values
$0,\ldots,\ell-1$
being the identity (plugging in the values
![]() $n=0,1,\ldots,\ell-1$
). The
$n=0,1,\ldots,\ell-1$
). The
![]() $\ell$
th Taylor coordinate is in
$\ell$
th Taylor coordinate is in
![]() $G_{\ell + j + 1}\cap\Gamma'$
, considering the value
$G_{\ell + j + 1}\cap\Gamma'$
, considering the value
![]() $n=\ell$
. Thus
$n=\ell$
. Thus
where
![]() $D^{-1}BC$
has the form
$D^{-1}BC$
has the form
 \[n\mapsto\prod_{i=\ell}^{s-j}g_{i+j}'^{\binom{n}{i}}\]
\[n\mapsto\prod_{i=\ell}^{s-j}g_{i+j}'^{\binom{n}{i}}\]
for
![]() $g_{i+j}'\in G_{i+j}\cap\Gamma$
and additionally
$g_{i+j}'\in G_{i+j}\cap\Gamma$
and additionally
![]() $g_{\ell+j}'\in G_{\ell+j+1}\cap\Gamma$
.
$g_{\ell+j}'\in G_{\ell+j+1}\cap\Gamma$
.
Note that
![]() $D^{-1}BC$
is of the correct form of Taylor series to apply the inductive hypothesis (since
$D^{-1}BC$
is of the correct form of Taylor series to apply the inductive hypothesis (since
![]() $g_{\ell+j}'\in G_{\ell+j+1}$
), yielding
$g_{\ell+j}'\in G_{\ell+j+1}$
), yielding
where M ranges over the
![]() $s-j-\ell$
“types” of level j elements of the Mal’cev basis of
$s-j-\ell$
“types” of level j elements of the Mal’cev basis of
![]() $H_0$
, from
$H_0$
, from
![]() $\ell+1$
to
$\ell+1$
to
![]() $s-j$
inclusive, and is arranged in the correct order within the product E, and
$s-j$
inclusive, and is arranged in the correct order within the product E, and
![]() $F\in H_{j+1}\cap\Gamma'$
. Finally, we may write
$F\in H_{j+1}\cap\Gamma'$
. Finally, we may write
and note that
![]() $H_{j+1}$
is normal in
$H_{j+1}$
is normal in
![]() $H_0$
due to the original prefiltration we established, so we find
$H_0$
due to the original prefiltration we established, so we find
![]() $E^{-1}(D^{-1}AD)E\in H_{j+1}\cap\Gamma'$
. Thus we have
$E^{-1}(D^{-1}AD)E\in H_{j+1}\cap\Gamma'$
. Thus we have
where D, E form the necessary ordered product for the Mal’cev second kind representation, and
![]() $F'\in H_{j+1}\cap\Gamma'$
. Finally, we recall the induction hypothesis for
$F'\in H_{j+1}\cap\Gamma'$
. Finally, we recall the induction hypothesis for
![]() $H_{j+1}\cap\Gamma'$
to finish.
$H_{j+1}\cap\Gamma'$
to finish.
Step 3. Semidirect product and Lie bracket structure constants. We now handle the generator Z. Note that given an element
![]() $(p,t)\in\operatorname{poly}(\mathbb{Z},\Gamma)\rtimes (K\mathbb{Z})$
, we may write
$(p,t)\in\operatorname{poly}(\mathbb{Z},\Gamma)\rtimes (K\mathbb{Z})$
, we may write
and therefore if Z was the highest element of the ordering (which would correspond to a situation where the filtration contains
![]() $H_1\rtimes\{0\}$
instead of
$H_1\rtimes\{0\}$
instead of
![]() $H_1\rtimes\mathbb{R}$
) we would easily be done. Instead, though, it is inserted right before the Mal’cev basis components for
$H_1\rtimes\mathbb{R}$
) we would easily be done. Instead, though, it is inserted right before the Mal’cev basis components for
![]() $H_1$
. Note however that
$H_1$
. Note however that
and recall that derivatives of polynomials in
![]() $H_j\cap\operatorname{poly}(\mathbb{Z},\Gamma)$
are in
$H_j\cap\operatorname{poly}(\mathbb{Z},\Gamma)$
are in
![]() $H_{j+1}\cap\operatorname{poly}(\mathbb{Z},\Gamma)$
due to the definitions of the shifted filtrations on G. Therefore we may commute
$H_{j+1}\cap\operatorname{poly}(\mathbb{Z},\Gamma)$
due to the definitions of the shifted filtrations on G. Therefore we may commute
![]() $(\operatorname{id}_G,t)$
across the product of the level 0 terms in the representation above, and we will introduce only terms of level 1 and higher (and they will lie in
$(\operatorname{id}_G,t)$
across the product of the level 0 terms in the representation above, and we will introduce only terms of level 1 and higher (and they will lie in
![]() $\widetilde{\Gamma}$
). Then using the Mal’cev representation for
$\widetilde{\Gamma}$
). Then using the Mal’cev representation for
![]() $H_1\cap\Gamma'$
finishes. This completes our discussion that the generators listed form a Mal’cev basis.
$H_1\cap\Gamma'$
finishes. This completes our discussion that the generators listed form a Mal’cev basis.
We now compute the Lie bracket structure constants associated to the Mal’cev basis. We will compute all structure constants via the identity
which holds for any Lie group and the associated Lie bracket.
We first compute the constants associated with Z. Note that
 \begin{align*}[Y_{i,k},Z] &= \frac{d}{dt_0}\frac{d}{dt_1}\big(n\mapsto \exp\!(t_0X_i)^{\binom{n}{k}},0\big)(\operatorname{id}_G,Kt_1)\big(n\mapsto \exp\!(t_0X_i)^{-\binom{n}{k}},0\big)(\operatorname{id}_G,-Kt_1)\bigg|_{t_0,t_1=0}\\&=\frac{d}{dt_0}\frac{d}{dt_1}\big(n\mapsto\exp\!(t_0X_i)^{\binom{n}{k}-\binom{n-Kt_1}{k}},0\big)\bigg|_{t_0,t_1=0}\\& = \log_{H_0\rtimes\mathbb{R}}\bigg(n\mapsto\exp\!(X_i)^{-\frac{d}{dt_1}\binom{n-Kt_1}{k}\big|_{t_0=0}},0\bigg)=\bigg(n\mapsto-\frac{d}{dt_1}\binom{n-Kt_1}{k}X_i\bigg|_{t_1=0},0\bigg),\end{align*}
\begin{align*}[Y_{i,k},Z] &= \frac{d}{dt_0}\frac{d}{dt_1}\big(n\mapsto \exp\!(t_0X_i)^{\binom{n}{k}},0\big)(\operatorname{id}_G,Kt_1)\big(n\mapsto \exp\!(t_0X_i)^{-\binom{n}{k}},0\big)(\operatorname{id}_G,-Kt_1)\bigg|_{t_0,t_1=0}\\&=\frac{d}{dt_0}\frac{d}{dt_1}\big(n\mapsto\exp\!(t_0X_i)^{\binom{n}{k}-\binom{n-Kt_1}{k}},0\big)\bigg|_{t_0,t_1=0}\\& = \log_{H_0\rtimes\mathbb{R}}\bigg(n\mapsto\exp\!(X_i)^{-\frac{d}{dt_1}\binom{n-Kt_1}{k}\big|_{t_0=0}},0\bigg)=\bigg(n\mapsto-\frac{d}{dt_1}\binom{n-Kt_1}{k}X_i\bigg|_{t_1=0},0\bigg),\end{align*}
where the last line follows from considering the relationship between the differential structure on
![]() $H_0$
and on G (which allows us to “implicitly differentiate in the obvious way”). The coefficients of
$H_0$
and on G (which allows us to “implicitly differentiate in the obvious way”). The coefficients of
![]() $({d}/{dt_1})\binom{n-Kt_1}{k}\big|_{t_1=0}$
are all integer multiples of
$({d}/{dt_1})\binom{n-Kt_1}{k}\big|_{t_1=0}$
are all integer multiples of
![]() $K^t/k!$
for
$K^t/k!$
for
![]() $1\le t\le k-1$
. We may easily express this in terms of various
$1\le t\le k-1$
. We may easily express this in terms of various
![]() $Y_{i,k'}$
for
$Y_{i,k'}$
for
![]() $k' \lt k$
, and the structure constants clearly have the desired form, lying in
$k' \lt k$
, and the structure constants clearly have the desired form, lying in
![]() $K(C_s)^{-1}\mathbb{Z}$
for an appropriate integer
$K(C_s)^{-1}\mathbb{Z}$
for an appropriate integer
![]() $C_s$
.
$C_s$
.
We next compute the structure constants associated with two polynomials. Notice that
 \begin{align*}&[Y_{i,k},Y_{j,\ell}]\\&= \frac{d}{dt_1}\frac{d}{dt_2}\big(n\mapsto \exp\!(t_1X_i)^{\binom{n}{k}},0\big)\big(n\mapsto \exp\!(t_2X_j)^{\binom{n}{\ell}},0\big)\big(n\mapsto \exp\!(t_1X_i)^{-\binom{n}{k}},0\big)\\ &\quad \times \big(n\mapsto \exp\!(t_2X_j)^{-\binom{n}{\ell}},0\big)\bigg|_{t_1,t_2=0}\\&=\frac{d}{dt_1}\frac{d}{dt_2} \bigg(n\mapsto \exp\bigg(t_1t_2\binom{n}{k}\binom{n}{\ell}[X_i,X_j]\bigg),0\bigg)\bigg|_{t_1,t_2=0}\\&=\bigg(n\mapsto\binom{n}{k}\binom{n}{\ell}[X_i,X_j],0\bigg).\end{align*}
\begin{align*}&[Y_{i,k},Y_{j,\ell}]\\&= \frac{d}{dt_1}\frac{d}{dt_2}\big(n\mapsto \exp\!(t_1X_i)^{\binom{n}{k}},0\big)\big(n\mapsto \exp\!(t_2X_j)^{\binom{n}{\ell}},0\big)\big(n\mapsto \exp\!(t_1X_i)^{-\binom{n}{k}},0\big)\\ &\quad \times \big(n\mapsto \exp\!(t_2X_j)^{-\binom{n}{\ell}},0\big)\bigg|_{t_1,t_2=0}\\&=\frac{d}{dt_1}\frac{d}{dt_2} \bigg(n\mapsto \exp\bigg(t_1t_2\binom{n}{k}\binom{n}{\ell}[X_i,X_j]\bigg),0\bigg)\bigg|_{t_1,t_2=0}\\&=\bigg(n\mapsto\binom{n}{k}\binom{n}{\ell}[X_i,X_j],0\bigg).\end{align*}
The second equality follows from using Baker–Campbell–Hausdorff to multiply the polynomial sequences (as pointwise functions, say) and collapse them, and then noting that we may discard terms with higher powers than
![]() $t_1^1$
and
$t_1^1$
and
![]() $t_2^1$
. The only relevant remaining term is the
$t_2^1$
. The only relevant remaining term is the
![]() $t_1t_2$
which has the claimed form.
$t_1t_2$
which has the claimed form.
Note that as
![]() $\binom{n}{k}\binom{n}{\ell}$
is an integer-valued polynomial, by Polya’s classification of integer polynomials [
Reference Pólya27
], it follows that this may be written as an integral combination of binomial coefficients with coefficients bounded by
$\binom{n}{k}\binom{n}{\ell}$
is an integer-valued polynomial, by Polya’s classification of integer polynomials [
Reference Pólya27
], it follows that this may be written as an integral combination of binomial coefficients with coefficients bounded by
![]() $O_s(1)$
. We obtain a representation in terms of various
$O_s(1)$
. We obtain a representation in terms of various
![]() $Y_{i',k'}$
where
$Y_{i',k'}$
where
![]() $k'\le k+\ell$
and
$k'\le k+\ell$
and
![]() $X_{i'}$
shows up in the expansion of
$X_{i'}$
shows up in the expansion of
![]() $[X_i,X_j]$
. We are done with this part of the proof, which includes verifying the well-definedness of various lifted filtrations, Mal’cev bases, and also the rationality properties of the Lie bracket structure constants.
$[X_i,X_j]$
. We are done with this part of the proof, which includes verifying the well-definedness of various lifted filtrations, Mal’cev bases, and also the rationality properties of the Lie bracket structure constants.
Step 4. Lifting the nilsequence and checking quantitative dependences. We now actually define the desired function. We are given a polynomial sequence g(x) and we define
![]() $q(x) = g(xN/K)$
. We define
$q(x) = g(xN/K)$
. We define
Note that
![]() $\widetilde{g}(x)$
is N-periodic as
$\widetilde{g}(x)$
is N-periodic as
![]() $\widetilde{g}(x+N)=\widetilde{g}(x)\ast(\operatorname{id}_G,K)$
. We now define
$\widetilde{g}(x+N)=\widetilde{g}(x)\ast(\operatorname{id}_G,K)$
. We now define
![]() $\widetilde{F}$
on
$\widetilde{F}$
on
![]() $\operatorname{poly}(\mathbb{R},G)/\operatorname{poly}(\mathbb{Z},\Gamma)\times [0,K)$
via
$\operatorname{poly}(\mathbb{R},G)/\operatorname{poly}(\mathbb{Z},\Gamma)\times [0,K)$
via
This extends uniquely to
![]() $H_0\rtimes\mathbb{R}$
if we enforce right-
$H_0\rtimes\mathbb{R}$
if we enforce right-
![]() $\widetilde{\Gamma}$
-invariance, which yields
$\widetilde{\Gamma}$
-invariance, which yields
That
![]() $\widetilde{F}$
is appropriately Lipschitz and that we can then descend this construction to a proper filtration will be checked last.
$\widetilde{F}$
is appropriately Lipschitz and that we can then descend this construction to a proper filtration will be checked last.
The key point is the following computation:
 \begin{align*}\widetilde{F}(\widetilde{g}(x)) &= \widetilde{F}((q,0)\ast (\operatorname{id}_G,Kx/N))=\widetilde{F}((q(\cdot + Kx/N),Kx/N))\\&=\phi(\{x/N\})F(q(Kx/N - K\lfloor x/N\rfloor))=\phi(\{x/N\})F(g(x - N\lfloor x/N\rfloor))\\&=\phi(\{x/N\})F(g(x \;\mathrm{mod}\;N)).\end{align*}
\begin{align*}\widetilde{F}(\widetilde{g}(x)) &= \widetilde{F}((q,0)\ast (\operatorname{id}_G,Kx/N))=\widetilde{F}((q(\cdot + Kx/N),Kx/N))\\&=\phi(\{x/N\})F(q(Kx/N - K\lfloor x/N\rfloor))=\phi(\{x/N\})F(g(x - N\lfloor x/N\rfloor))\\&=\phi(\{x/N\})F(g(x \;\mathrm{mod}\;N)).\end{align*}
We now check that the function
![]() $|\widetilde{F}|$
is appropriately Lipschitz with respect to the Mal’cev basis specified. Since
$|\widetilde{F}|$
is appropriately Lipschitz with respect to the Mal’cev basis specified. Since
![]() $\widetilde{F}$
is bounded by
$\widetilde{F}$
is bounded by
![]() $\lVert F\rVert_{\infty}\lVert\phi\rVert_{\infty}$
, note that for
$\lVert F\rVert_{\infty}\lVert\phi\rVert_{\infty}$
, note that for
![]() $x,y\in (H_0\rtimes \mathbb{R})/\widetilde{\Gamma}$
if
$x,y\in (H_0\rtimes \mathbb{R})/\widetilde{\Gamma}$
if
![]() $d_{(H_0\rtimes \mathbb{R})/\widetilde{\Gamma}}(x,y)\ge \varepsilon$
we have
$d_{(H_0\rtimes \mathbb{R})/\widetilde{\Gamma}}(x,y)\ge \varepsilon$
we have
Fix
![]() $\varepsilon\le O_K(M)^{-O_s(d)^{O_s(1)}}$
to be chosen later. The diameter of
$\varepsilon\le O_K(M)^{-O_s(d)^{O_s(1)}}$
to be chosen later. The diameter of
![]() $(H_0\rtimes \mathbb{R})/(\operatorname{poly}(\mathbb{Z},\Gamma)\rtimes K\mathbb{Z})$
is bounded by
$(H_0\rtimes \mathbb{R})/(\operatorname{poly}(\mathbb{Z},\Gamma)\rtimes K\mathbb{Z})$
is bounded by
![]() $O_K(M)^{O_s(d)^{O_s(1)}}$
by [
Reference Leng22
, lemma B·8]Footnote
1
, so there exist
$O_K(M)^{O_s(d)^{O_s(1)}}$
by [
Reference Leng22
, lemma B·8]Footnote
1
, so there exist
![]() $\widetilde{x},\widetilde{y}$
such that
$\widetilde{x},\widetilde{y}$
such that
Furthermore we may chose the fundamental representatives
![]() $\widetilde{x}$
and
$\widetilde{x}$
and
![]() $\widetilde{y}$
such that the second coordinate is in [0,K) (by multiplying by an appropriate element of
$\widetilde{y}$
such that the second coordinate is in [0,K) (by multiplying by an appropriate element of
![]() $\operatorname{Id}_{G}\rtimes(K\mathbb{Z})$
on the right and noting that the metric is right-invariant). Note that if the second coordinate of the representative
$\operatorname{Id}_{G}\rtimes(K\mathbb{Z})$
on the right and noting that the metric is right-invariant). Note that if the second coordinate of the representative
![]() $\widetilde{x}$
is outside the range
$\widetilde{x}$
is outside the range
![]() $[1/4,2/3]$
, the assumption on the support of
$[1/4,2/3]$
, the assumption on the support of
![]() $\phi$
guarantees that
$\phi$
guarantees that
![]() $\widetilde{F}(\widetilde{x}\Gamma) = \widetilde{F}(\widetilde{y}\Gamma) = 0$
and therefore verifying the Lipschitz constant in this case is trivial. (This uses that
$\widetilde{F}(\widetilde{x}\Gamma) = \widetilde{F}(\widetilde{y}\Gamma) = 0$
and therefore verifying the Lipschitz constant in this case is trivial. (This uses that
![]() $\varepsilon$
is sufficiently small.)
$\varepsilon$
is sufficiently small.)
Else we denote
![]() $\widetilde{x} = (x^{\ast},x')$
with
$\widetilde{x} = (x^{\ast},x')$
with
![]() $x^{\ast}\in H_0$
and
$x^{\ast}\in H_0$
and
![]() $x'\in[1/4,2/3]$
and
$x'\in[1/4,2/3]$
and
![]() $\widetilde{y}$
analogously. We now have
$\widetilde{y}$
analogously. We now have
Let
![]() $\psi$
denote the second Mal’cev coordinates with respect to the basis specified for
$\psi$
denote the second Mal’cev coordinates with respect to the basis specified for
![]() $(H_0\rtimes \mathbb{R})/\widetilde{\Gamma}$
. Note that x
′,y
′ are controlled only by Z in the Mal’cev basis and thus we can bound the second term by
$(H_0\rtimes \mathbb{R})/\widetilde{\Gamma}$
. Note that x
′,y
′ are controlled only by Z in the Mal’cev basis and thus we can bound the second term by
To bound the first term, note that
![]() $d_{G/\Gamma}(x^{\ast}(0)\Gamma,y^{\ast}(0)\Gamma)\le d_G(x^{\ast}(0),y^{\ast}(0))$
.
$d_{G/\Gamma}(x^{\ast}(0)\Gamma,y^{\ast}(0)\Gamma)\le d_G(x^{\ast}(0),y^{\ast}(0))$
.
Let
![]() $\widetilde{x} = \exp\!((x'/K)Z)\prod_{k,\ell}\exp\!(x_{k,\ell}Y_{k,\ell})$
and analogously for
$\widetilde{x} = \exp\!((x'/K)Z)\prod_{k,\ell}\exp\!(x_{k,\ell}Y_{k,\ell})$
and analogously for
![]() $\widetilde{y}$
where the product over
$\widetilde{y}$
where the product over
![]() $Y_{k,\ell}$
is taken in the ordering specified for the Mal’cev basis. We have
$Y_{k,\ell}$
is taken in the ordering specified for the Mal’cev basis. We have
Note that the only terms which contribute to the above product are
![]() $Y_{k,0} = (n\mapsto \binom{n}{0}X_k) = (n\mapsto X_k)$
. If
$Y_{k,0} = (n\mapsto \binom{n}{0}X_k) = (n\mapsto X_k)$
. If
![]() $X_k\in \mathfrak{g}_{j}\setminus \mathfrak{g}_{j+1}$
, this has level precisely j and thus the product (removing terms which are the identity) are in the correct order for the Mal’cev basis on G.
$X_k\in \mathfrak{g}_{j}\setminus \mathfrak{g}_{j+1}$
, this has level precisely j and thus the product (removing terms which are the identity) are in the correct order for the Mal’cev basis on G.
Therefore we have
 \begin{align*}d_{G}(x^{\ast}(0),y^{\ast}(0)) &\le O_K(M)^{O_s(d^{O_s(1)})}\max_{k}|x_{k,0}-y_{k,0}|\\&\le O_K(M)^{O_s(d^{O_s(1)})}\big(\max_{k,\ell}|x_{k,\ell}-y_{k,\ell}| + |x'/K-y'/K|\big)\\&\le O_K(M)^{O_s(d^{O_s(1)})}d_{H_0\rtimes \mathbb{R}}(\widetilde{x},\widetilde{y}).\end{align*}
\begin{align*}d_{G}(x^{\ast}(0),y^{\ast}(0)) &\le O_K(M)^{O_s(d^{O_s(1)})}\max_{k}|x_{k,0}-y_{k,0}|\\&\le O_K(M)^{O_s(d^{O_s(1)})}\big(\max_{k,\ell}|x_{k,\ell}-y_{k,\ell}| + |x'/K-y'/K|\big)\\&\le O_K(M)^{O_s(d^{O_s(1)})}d_{H_0\rtimes \mathbb{R}}(\widetilde{x},\widetilde{y}).\end{align*}
The first line follows from [
Reference Leng22
, lemma B·3] applied on the Mal’cev basis
![]() $\mathcal{X}$
of G and the second inequality is trivial. The final inequality follows from [
Reference Leng22
, lemma B·3] and that
$\mathcal{X}$
of G and the second inequality is trivial. The final inequality follows from [
Reference Leng22
, lemma B·3] and that
![]() $\max_{k,\ell}|x_{k,0}-y_{k,0}| + |x'/K-y'/K|$
corresponds (up to constants) to the
$\max_{k,\ell}|x_{k,0}-y_{k,0}| + |x'/K-y'/K|$
corresponds (up to constants) to the
![]() $L^{\infty}$
distance in the Mal’cev coordinates when Z is placed first in the order and one may return to the original distance at the cost of
$L^{\infty}$
distance in the Mal’cev coordinates when Z is placed first in the order and one may return to the original distance at the cost of
![]() $O_K(M)^{O_s(d)^{O_s(1)}}$
by [
Reference Leng22
, lemma B·3]. (Shifting Z to the first position is clearly a 1-rational change of basis.)
$O_K(M)^{O_s(d)^{O_s(1)}}$
by [
Reference Leng22
, lemma B·3]. (Shifting Z to the first position is clearly a 1-rational change of basis.)
Step 5. Reducing to a proper filtration. We now (finally) perform the last reduction to place our polynomial sequence on a proper filtration. By inspection we have
with
![]() $h_i^{\ast}\in H_i\rtimes \mathbb{R}$
for
$h_i^{\ast}\in H_i\rtimes \mathbb{R}$
for
![]() $i\le 1$
. Let
$i\le 1$
. Let
![]() $h_0^{\ast} = \{h_0^{\ast}\}[h_0^\ast]$
such that
$h_0^{\ast} = \{h_0^{\ast}\}[h_0^\ast]$
such that
![]() $[h_0^\ast]\in\widetilde{\Gamma}$
and
$[h_0^\ast]\in\widetilde{\Gamma}$
and
![]() $\lVert\psi(\{h_0^{\ast}\})\rVert\le 1$
.
$\lVert\psi(\{h_0^{\ast}\})\rVert\le 1$
.
For
![]() $\widetilde{p}\in H_1\rtimes\mathbb{R}$
define
$\widetilde{p}\in H_1\rtimes\mathbb{R}$
define
![]() $F^{\ast}(\widetilde{p}\widetilde{\Gamma}) = \widetilde{F}(\{h_0^{\ast}\}\widetilde{p}\widetilde{\Gamma})$
, and note that
$F^{\ast}(\widetilde{p}\widetilde{\Gamma}) = \widetilde{F}(\{h_0^{\ast}\}\widetilde{p}\widetilde{\Gamma})$
, and note that
 \begin{align*}\widetilde{F}(\widetilde{g}(x)\widetilde{\Gamma}) &= \widetilde{F}(\{h_0^{\ast}\}[h_0^\ast](h_1^{\ast})^{\binom{x}{1}}\widetilde{\Gamma})=\widetilde{F}(\{h_0^{\ast}\}([h_0^\ast]h_1^{\ast}[h_0^\ast]^{-1})^{\binom{x}{1}}[h_0^\ast]\widetilde{\Gamma})\\&= F^{\ast}(([h_0^\ast]h_1^{\ast}[h_0^\ast]^{-1})^{\binom{x}{1}}\widetilde{\Gamma}).\end{align*}
\begin{align*}\widetilde{F}(\widetilde{g}(x)\widetilde{\Gamma}) &= \widetilde{F}(\{h_0^{\ast}\}[h_0^\ast](h_1^{\ast})^{\binom{x}{1}}\widetilde{\Gamma})=\widetilde{F}(\{h_0^{\ast}\}([h_0^\ast]h_1^{\ast}[h_0^\ast]^{-1})^{\binom{x}{1}}[h_0^\ast]\widetilde{\Gamma})\\&= F^{\ast}(([h_0^\ast]h_1^{\ast}[h_0^\ast]^{-1})^{\binom{x}{1}}\widetilde{\Gamma}).\end{align*}
Since left-multiplication by bounded elements is suitably Lipschitz and since
![]() $H_1\rtimes \mathbb{R}$
is normal in
$H_1\rtimes \mathbb{R}$
is normal in
![]() $H_0\rtimes \mathbb{R}$
, we have that
$H_0\rtimes \mathbb{R}$
, we have that
![]() $([h_0^\ast]h_1^{\ast}[h_0^\ast]^{-1})^{\binom{x}{1}}$
is a polynomial sequence with respect to the filtration
$([h_0^\ast]h_1^{\ast}[h_0^\ast]^{-1})^{\binom{x}{1}}$
is a polynomial sequence with respect to the filtration
![]() $H_1\rtimes \mathbb{R} = H_1\rtimes \mathbb{R}\geqslant H_2\rtimes \{0\}\geqslant \cdots \geqslant H_s\rtimes \{0\} \geqslant \operatorname{Id}_{H_1\rtimes \mathbb{R}}$
.
$H_1\rtimes \mathbb{R} = H_1\rtimes \mathbb{R}\geqslant H_2\rtimes \{0\}\geqslant \cdots \geqslant H_s\rtimes \{0\} \geqslant \operatorname{Id}_{H_1\rtimes \mathbb{R}}$
.
Note that pre- or post-multiplication by a fixed constant does not change N-periodicity. Furthermore note that Z and all level 1 and higher elements in the order given by removing all level 0 elements gives a valid Mal’cev basis with respect to the proper filtration
Thus the polynomial sequence
![]() $([h_0]h_1^{\ast}[h_0]^{-1})^{\binom{x}{1}}$
with respect to the function
$([h_0]h_1^{\ast}[h_0]^{-1})^{\binom{x}{1}}$
with respect to the function
![]() $\widetilde{F}(\cdot)$
on nilmanifold
$\widetilde{F}(\cdot)$
on nilmanifold
![]() $(H_1\rtimes\mathbb{R})/(\widetilde{\Gamma}\cap(H_1\rtimes\mathbb{R}))$
with this filtration and Mal’cev basis provides the desired construction.
$(H_1\rtimes\mathbb{R})/(\widetilde{\Gamma}\cap(H_1\rtimes\mathbb{R}))$
with this filtration and Mal’cev basis provides the desired construction.
Appendix D. Deferred lemmas
We first prove the necessary partition of unity result on a nilmanifold.
Proof of Lemma 2·4. The key trick is to consider a “smoothed sum” of fundamental domains and perform a partition of unity. Let
![]() $\delta$
be a constant to be specified later and let
$\delta$
be a constant to be specified later and let
![]() $f(x)\ge 0$
be a smooth bump function on
$f(x)\ge 0$
be a smooth bump function on
![]() $\mathbb{R}$
with
$\mathbb{R}$
with
![]() $\operatorname{supp}(f)\in[\!-\!1/4,1/4]$
,
$\operatorname{supp}(f)\in[\!-\!1/4,1/4]$
,
![]() $\int_{\mathbb{R}}f(x)dx = 1$
, and
$\int_{\mathbb{R}}f(x)dx = 1$
, and
![]() $\lVert f\rVert_{\infty}\le O(1)$
. Let
$\lVert f\rVert_{\infty}\le O(1)$
. Let
![]() $H_j$
be smooth functions indexed by
$H_j$
be smooth functions indexed by
![]() $j\in S$
of size
$j\in S$
of size
![]() $O(1/\delta)$
which are nonnegative with
$O(1/\delta)$
which are nonnegative with
![]() $\operatorname{supp}(H_j)\in [j\delta,(j+2)\delta]$
,
$\operatorname{supp}(H_j)\in [j\delta,(j+2)\delta]$
,
![]() $\lVert H_j\rVert_{\infty}\le O(1)$
, and
$\lVert H_j\rVert_{\infty}\le O(1)$
, and
![]() $\sum_{j\in S}H_j(x)$
equal to 1 for
$\sum_{j\in S}H_j(x)$
equal to 1 for
![]() $|x|\le 3/2$
and 0 for
$|x|\le 3/2$
and 0 for
![]() $|x|\ge 2$
.
$|x|\ge 2$
.
For each
![]() $g\in G$
and
$g\in G$
and
![]() $\beta\in\mathbb{R}$
, there exists a unique
$\beta\in\mathbb{R}$
, there exists a unique
![]() $\gamma_i\in\Gamma$
such that
$\gamma_i\in\Gamma$
such that
![]() $\psi(g\gamma_i)\in[\!-\!\beta,1-\beta)^d$
(see e.g. [
Reference Leng22
, lemma B·6]). Define for
$\psi(g\gamma_i)\in[\!-\!\beta,1-\beta)^d$
(see e.g. [
Reference Leng22
, lemma B·6]). Define for
![]() $\beta\in\mathbb{R}$
the function
$\beta\in\mathbb{R}$
the function
![]() $T_{\beta}\colon G\to\Gamma$
such that
$T_{\beta}\colon G\to\Gamma$
such that
![]() $\psi(gT_\beta(g))\in[\!-\!\beta,1-\beta)^d$
; note that this function suffers from discontinuities at the boundaries of
$\psi(gT_\beta(g))\in[\!-\!\beta,1-\beta)^d$
; note that this function suffers from discontinuities at the boundaries of
![]() $[\!-\!\beta,1-\beta)^d$
.
$[\!-\!\beta,1-\beta)^d$
.
Note that for all
![]() $g\in G$
we have
$g\in G$
we have
 \begin{align*}1 &= \int_{\beta\in\mathbb{R}}f(\beta)d\beta=\int_{\beta\in \mathbb{R}}\prod_{i=1}^{d}\bigg(\sum_{j\in S}H_j(\psi_i(gT_{\beta}(g)))\bigg)f(\beta)d\beta\\&=\sum_{j_1,\ldots,j_d\in S}\int_{\beta\in\mathbb{R}} \prod_{k=1}^{d}H_{j_k}(\psi_k(gT_{\beta}(g)))f(\beta)d\beta.\end{align*}
\begin{align*}1 &= \int_{\beta\in\mathbb{R}}f(\beta)d\beta=\int_{\beta\in \mathbb{R}}\prod_{i=1}^{d}\bigg(\sum_{j\in S}H_j(\psi_i(gT_{\beta}(g)))\bigg)f(\beta)d\beta\\&=\sum_{j_1,\ldots,j_d\in S}\int_{\beta\in\mathbb{R}} \prod_{k=1}^{d}H_{j_k}(\psi_k(gT_{\beta}(g)))f(\beta)d\beta.\end{align*}
The functions in our collection will be indexed by
![]() $j_1,\ldots,j_d$
and are defined by
$j_1,\ldots,j_d$
and are defined by
 \[\tau_{j_1,\ldots,j_d}(g\Gamma) = \int_{\beta\in\mathbb{R}}\prod_{k=1}^{d}H_{j_k}(\psi_k(gT_{\beta}(g)))f(\beta)d\beta.\]
\[\tau_{j_1,\ldots,j_d}(g\Gamma) = \int_{\beta\in\mathbb{R}}\prod_{k=1}^{d}H_{j_k}(\psi_k(gT_{\beta}(g)))f(\beta)d\beta.\]
This is a well-defined function since
![]() $gT_{\beta}(g) = g\gamma T_{\beta}(g\gamma)$
for all
$gT_{\beta}(g) = g\gamma T_{\beta}(g\gamma)$
for all
![]() $\gamma\in\Gamma$
. Furthermore note that
$\gamma\in\Gamma$
. Furthermore note that
![]() $\lVert\tau_{j_1,\ldots,j_d}\rVert_{\infty}\le\exp\!(O(d))$
. We will use these as our partition of unity.
$\lVert\tau_{j_1,\ldots,j_d}\rVert_{\infty}\le\exp\!(O(d))$
. We will use these as our partition of unity.
Let
![]() $L = O(M)^{O_s(d^{O_s(1)})}$
with implicit constants chosen sufficiently large. To check the Lipschitz property, it suffices to consider
$L = O(M)^{O_s(d^{O_s(1)})}$
with implicit constants chosen sufficiently large. To check the Lipschitz property, it suffices to consider
![]() $x\Gamma, y\Gamma$
such that
$x\Gamma, y\Gamma$
such that
![]() $d_{G/\Gamma}(x\Gamma, y\Gamma)\le L^{-1}$
. We may find
$d_{G/\Gamma}(x\Gamma, y\Gamma)\le L^{-1}$
. We may find
![]() $\widetilde{x},\widetilde{y}\in G$
such that
$\widetilde{x},\widetilde{y}\in G$
such that
If
![]() $d_G(\gamma,\operatorname{id}_G)\ge L^3$
then note that for
$d_G(\gamma,\operatorname{id}_G)\ge L^3$
then note that for
![]() $g\in G$
with
$g\in G$
with
![]() $d_G(g,\operatorname{id}_G)\le L$
we have
$d_G(g,\operatorname{id}_G)\le L$
we have
using quantitative approximate left-invariance of the metric ([
Reference Leng22
, lemma B·4]). Therefore we have
![]() $d_{G}(T_\beta(\widetilde{x}),\operatorname{id}_G) + d_{G}(T_\beta(\widetilde{y}),\operatorname{id}_G)\le 2L^3$
for
$d_{G}(T_\beta(\widetilde{x}),\operatorname{id}_G) + d_{G}(T_\beta(\widetilde{y}),\operatorname{id}_G)\le 2L^3$
for
![]() $|\beta|\le 2$
. Let
$|\beta|\le 2$
. Let
![]() $\widetilde{\Gamma}\subseteq\Gamma$
be the set of all
$\widetilde{\Gamma}\subseteq\Gamma$
be the set of all
![]() $\widetilde{\gamma}\in\Gamma$
such that
$\widetilde{\gamma}\in\Gamma$
such that
![]() $d_{G}(\widetilde{\gamma},\operatorname{id}_G)\le 2L^3$
and note that
$d_{G}(\widetilde{\gamma},\operatorname{id}_G)\le 2L^3$
and note that
![]() $|\widetilde{\Gamma}|\le L^{O_s(d^{O_s(1)})}$
.
$|\widetilde{\Gamma}|\le L^{O_s(d^{O_s(1)})}$
.
We now show the desired properties of a partition of unity. Let
![]() $\beta$
be drawn from the probability distribution
$\beta$
be drawn from the probability distribution
![]() $f(\beta)$
. Let
$f(\beta)$
. Let
![]() $\eta\;:\!=\; d_{G}(\widetilde{x},\widetilde{y})$
and note that for
$\eta\;:\!=\; d_{G}(\widetilde{x},\widetilde{y})$
and note that for
![]() $\gamma\in \widetilde{\Gamma}$
we have
$\gamma\in \widetilde{\Gamma}$
we have
![]() $\lVert\psi(\widetilde{x}\gamma)-\psi(\widetilde{y}\gamma)\rVert\le \eta\cdot L^{O_s(d^{O_s(1)})}=:\eta'$
. Therefore
$\lVert\psi(\widetilde{x}\gamma)-\psi(\widetilde{y}\gamma)\rVert\le \eta\cdot L^{O_s(d^{O_s(1)})}=:\eta'$
. Therefore
 \begin{align*}&\mathbb{P}_{\beta}[T_{\beta}(\widetilde{x})\neq T_{\beta}(\widetilde{y})] \le \sum_{\gamma\in \widetilde{\Gamma}}\mathbb{P}_{\beta}[\psi(\widetilde{x}\gamma)\in [\!-\!\beta,1-\beta)^{d} \cap \psi(\widetilde{y}\widetilde{x}^{-1}(\widetilde{x}\gamma))\notin [\!-\!\beta,1-\beta)^{d}]\\&\quad \le \sum_{\gamma\in \widetilde{\Gamma}}\sum_{i=1}^{d}\mathbb{P}_{\beta}[\psi_i(\widetilde{x}\gamma)\in [\!-\!\beta - \eta',-\beta]\cup [1-\beta-\eta',1-\beta)]\le\eta\delta^{-1}L^{O_s(d^{O_s(1)})}.\end{align*}
\begin{align*}&\mathbb{P}_{\beta}[T_{\beta}(\widetilde{x})\neq T_{\beta}(\widetilde{y})] \le \sum_{\gamma\in \widetilde{\Gamma}}\mathbb{P}_{\beta}[\psi(\widetilde{x}\gamma)\in [\!-\!\beta,1-\beta)^{d} \cap \psi(\widetilde{y}\widetilde{x}^{-1}(\widetilde{x}\gamma))\notin [\!-\!\beta,1-\beta)^{d}]\\&\quad \le \sum_{\gamma\in \widetilde{\Gamma}}\sum_{i=1}^{d}\mathbb{P}_{\beta}[\psi_i(\widetilde{x}\gamma)\in [\!-\!\beta - \eta',-\beta]\cup [1-\beta-\eta',1-\beta)]\le\eta\delta^{-1}L^{O_s(d^{O_s(1)})}.\end{align*}
Thus
 \begin{align*}\bigg|\tau_{j_1,\ldots,j_d}(\widetilde{x}\Gamma) - \tau_{j_1,\ldots,j_d}(\widetilde{y}\Gamma)\bigg|&\le \int_{\beta\in \mathbb{R}}\bigg| \prod_{k=1}^{d}H_{j_k}(\psi(\widetilde{x}T_{\beta}(\widetilde{x}))) - \prod_{k=1}^{d}H_{j_k}(\psi(\widetilde{y}T_{\beta}(\widetilde{x})))\bigg|f(\beta)d\beta \\&\qquad\qquad+\delta^{-O(d)}\cdot \mathbb{P}_{\beta}[T_{\beta}(\widetilde{x})\neq T_{\beta}(\widetilde{y})]\\&\le \delta^{-O(d)}\eta L^{O_s(d^{O_s(1)})},\end{align*}
\begin{align*}\bigg|\tau_{j_1,\ldots,j_d}(\widetilde{x}\Gamma) - \tau_{j_1,\ldots,j_d}(\widetilde{y}\Gamma)\bigg|&\le \int_{\beta\in \mathbb{R}}\bigg| \prod_{k=1}^{d}H_{j_k}(\psi(\widetilde{x}T_{\beta}(\widetilde{x}))) - \prod_{k=1}^{d}H_{j_k}(\psi(\widetilde{y}T_{\beta}(\widetilde{x})))\bigg|f(\beta)d\beta \\&\qquad\qquad+\delta^{-O(d)}\cdot \mathbb{P}_{\beta}[T_{\beta}(\widetilde{x})\neq T_{\beta}(\widetilde{y})]\\&\le \delta^{-O(d)}\eta L^{O_s(d^{O_s(1)})},\end{align*}
which demonstrates the necessary Lipschitz bound.
Finally we check the supports; note that in order for
![]() $\tau_{j_1,\ldots,j_d}(g\Gamma)$
to be nonzero, there exists
$\tau_{j_1,\ldots,j_d}(g\Gamma)$
to be nonzero, there exists
![]() $\gamma\in\Gamma$
such that
$\gamma\in\Gamma$
such that
![]() $\psi(g\gamma) \in \prod_{k=1}^{d}[j_k\delta,(j_k+2)\delta]$
. Let
$\psi(g\gamma) \in \prod_{k=1}^{d}[j_k\delta,(j_k+2)\delta]$
. Let
![]() $\widetilde{g}$
be such that
$\widetilde{g}$
be such that
![]() $\psi(\widetilde{g}) = ((j_k+1)\delta)_{1\le k\le d}\in[\!-\!2,2]^{d}$
. We have
$\psi(\widetilde{g}) = ((j_k+1)\delta)_{1\le k\le d}\in[\!-\!2,2]^{d}$
. We have
![]() $\lVert\psi(g\gamma)-\psi(\widetilde{g})\rVert\le\delta$
. Thus, taking the fundamental domain for
$\lVert\psi(g\gamma)-\psi(\widetilde{g})\rVert\le\delta$
. Thus, taking the fundamental domain for
![]() $G/\Gamma$
which is
$G/\Gamma$
which is
![]() $\prod_{k=1}^{d}[(j_k+1)\delta-1/2,(j_k+1)\delta+1/2)$
(with respect to
$\prod_{k=1}^{d}[(j_k+1)\delta-1/2,(j_k+1)\delta+1/2)$
(with respect to
![]() $\psi$
) we have that the support is contained within a
$\psi$
) we have that the support is contained within a
![]() $\delta$
-ball of the center. Note as
$\delta$
-ball of the center. Note as
![]() $\psi_{\exp}\circ \psi^{-1}$
is a polynomial with coefficients bounded by
$\psi_{\exp}\circ \psi^{-1}$
is a polynomial with coefficients bounded by
![]() $O(M)^{O_s(d^{O_s(1)})}$
and degree
$O(M)^{O_s(d^{O_s(1)})}$
and degree
![]() $O_s(1)$
([
Reference Leng22
, lemma B·1]) we have the desired result taking
$O_s(1)$
([
Reference Leng22
, lemma B·1]) we have the desired result taking
![]() $\delta = \varepsilon M^{-O_s(d^{O_s(1)})}$
(and appropriately modifying the definition of L).
$\delta = \varepsilon M^{-O_s(d^{O_s(1)})}$
(and appropriately modifying the definition of L).
We next need that sufficiently divisible structure constants prove that
![]() $\psi_{\exp}^{-1}(\Gamma)$
.
$\psi_{\exp}^{-1}(\Gamma)$
.
Proof of Lemma 2·5. First, consider any element of
![]() $\Gamma$
which can be written
$\Gamma$
which can be written
![]() $\gamma=\prod_{i=1}^{d}\exp\!(t_iX_i)$
for
$\gamma=\prod_{i=1}^{d}\exp\!(t_iX_i)$
for
![]() $t_i\in\mathbb{Z}$
. We inductively prove that
$t_i\in\mathbb{Z}$
. We inductively prove that
![]() $\prod_{i=j}^d\exp\!(t_iX_i)$
is in
$\prod_{i=j}^d\exp\!(t_iX_i)$
is in
![]() $\psi_{\exp}^{-1}(\mathbb{Z}^d)$
. Suppose we have shown that
$\psi_{\exp}^{-1}(\mathbb{Z}^d)$
. Suppose we have shown that
![]() $\prod_{i=j+1}^{d}\exp\!(t_iX_i) = \exp\!(\sum_{i=j+1}^{d}u_iX_i)$
with
$\prod_{i=j+1}^{d}\exp\!(t_iX_i) = \exp\!(\sum_{i=j+1}^{d}u_iX_i)$
with
![]() $u_i\in\mathbb{Z}$
, for some
$u_i\in\mathbb{Z}$
, for some
![]() $1\le j\le d-1$
(the base case
$1\le j\le d-1$
(the base case
![]() $j=d-1$
is obvious). Then
$j=d-1$
is obvious). Then
 \[\prod_{i=j}^{d}\exp\!(t_iX_i)= \exp\!(t_jX_j)\exp\bigg(\sum_{i=j+1}^{d}u_iX_i\bigg) = \exp\bigg(t_jX_j + \sum_{i=j+1}^{d}u_iX_i + \cdots\bigg),\]
\[\prod_{i=j}^{d}\exp\!(t_iX_i)= \exp\!(t_jX_j)\exp\bigg(\sum_{i=j+1}^{d}u_iX_i\bigg) = \exp\bigg(t_jX_j + \sum_{i=j+1}^{d}u_iX_i + \cdots\bigg),\]
where the remainder is a finite list of commutators of
![]() $t_jX_j$
and
$t_jX_j$
and
![]() $\sum_{i=j+1}^{d}u_iX_i$
coming from the Baker–Campbell–Hausdorff formula. As the coefficients are rationals with denominators bounded by
$\sum_{i=j+1}^{d}u_iX_i$
coming from the Baker–Campbell–Hausdorff formula. As the coefficients are rationals with denominators bounded by
![]() $C_s$
, it follows immediately from the condition on divisibility of Lie bracket structure constants that the inductive step holds. We deduce
$C_s$
, it follows immediately from the condition on divisibility of Lie bracket structure constants that the inductive step holds. We deduce
![]() $\psi_{\exp}(\Gamma)\subseteq\mathbb{Z}^d$
.
$\psi_{\exp}(\Gamma)\subseteq\mathbb{Z}^d$
.
For the reverse inclusion, we also use induction. We show for all
![]() $1\le j\le d-1$
that for any
$1\le j\le d-1$
that for any
![]() $u_i\in\mathbb{Z}$
,
$u_i\in\mathbb{Z}$
,
![]() $\exp\!(\sum_{i=j}^du_iX_i)$
can be written in the form
$\exp\!(\sum_{i=j}^du_iX_i)$
can be written in the form
![]() $\prod_{i=j}^d\exp\!(t_iX_i)$
for
$\prod_{i=j}^d\exp\!(t_iX_i)$
for
![]() $t_i\in\mathbb{Z}$
. Suppose we have the result for
$t_i\in\mathbb{Z}$
. Suppose we have the result for
![]() $j+1$
, so that we have
$j+1$
, so that we have
![]() $\exp\!(\sum_{i=j+1}^{d}u_iX_i) = \prod_{i=j+1}^{d}\exp\!(t_iX_i)$
. Then
$\exp\!(\sum_{i=j+1}^{d}u_iX_i) = \prod_{i=j+1}^{d}\exp\!(t_iX_i)$
. Then
 \[\exp\!(\!-\!u_jX_j)\exp\bigg(\sum_{i=j}^{d}u_iX_i\bigg) = \exp\bigg(\sum_{i=j+1}^{d}u_i'X_i\bigg)\]
\[\exp\!(\!-\!u_jX_j)\exp\bigg(\sum_{i=j}^{d}u_iX_i\bigg) = \exp\bigg(\sum_{i=j+1}^{d}u_i'X_i\bigg)\]
for
![]() $u_i'\in\mathbb{Z}$
using the Baker–Campbell–Hausdorff formula, the divisibility assumption, and the filtered nature of the Mal’cev basis. (The term on the far left is tailored to cancel the
$u_i'\in\mathbb{Z}$
using the Baker–Campbell–Hausdorff formula, the divisibility assumption, and the filtered nature of the Mal’cev basis. (The term on the far left is tailored to cancel the
![]() $X_j$
part.) Again, the inductive step immediately follows. This demonstrates
$X_j$
part.) Again, the inductive step immediately follows. This demonstrates
![]() $\psi_{\exp}^{-1}(\mathbb{Z}^d)\subseteq\Gamma$
, and we are done.
$\psi_{\exp}^{-1}(\mathbb{Z}^d)\subseteq\Gamma$
, and we are done.
We next prove a comparison estimate between the distance in Mal’cev coordinates of the first kind and the associated torus metric.
Proof of Lemma 2·6. Note that
As
![]() $\psi\circ\psi_{\exp}^{-1}$
is a polynomial of degree
$\psi\circ\psi_{\exp}^{-1}$
is a polynomial of degree
![]() $O_s(1)$
with coefficients bounded by
$O_s(1)$
with coefficients bounded by
![]() $O(M)^{O_s(d^{O_s(1)})}$
([
Reference Leng22
, lemma B·1]) we have that
$O(M)^{O_s(d^{O_s(1)})}$
([
Reference Leng22
, lemma B·1]) we have that
The result then follows from [ Reference Leng22 , lemma B·3].
We now give the short proof of Lemma 2·8.
Proof of Lemma 2·8. It is evidently enough to show it for two functions
![]() $f_1,f_2$
. Additionally, recall the product rule
$f_1,f_2$
. Additionally, recall the product rule
where
![]() $T_hg(x)=g(x+h)$
defines the translation operator. Note that all translation operators commute with all other operations such as discrete derivatives and products, and other translations. Also, this is valid at a point x so long as
$T_hg(x)=g(x+h)$
defines the translation operator. Note that all translation operators commute with all other operations such as discrete derivatives and products, and other translations. Also, this is valid at a point x so long as
![]() $x,x+h$
are in the domains of f, g.
$x,x+h$
are in the domains of f, g.
Let
![]() $s=d_1+d_2$
. Suppose we are given
$s=d_1+d_2$
. Suppose we are given
![]() $x,h_1,\ldots,h_{s+1}$
with
$x,h_1,\ldots,h_{s+1}$
with
![]() $x+\{0,h_1\}+\cdots+\{0,h_{s+1}\}\subseteq S$
. We have, by iterating (D·1),
$x+\{0,h_1\}+\cdots+\{0,h_{s+1}\}\subseteq S$
. We have, by iterating (D·1),
This is seen to be valid since every element of the cube
![]() $x+\{0,h_1\}+\cdots+\{0,h_{s+1}\}$
is in the domain S. Now, for every disjoint partition
$x+\{0,h_1\}+\cdots+\{0,h_{s+1}\}$
is in the domain S. Now, for every disjoint partition
![]() $T_1\sqcup T_2=[s+1]$
we have either
$T_1\sqcup T_2=[s+1]$
we have either
![]() $|T_1|\ge d_1+1$
or
$|T_1|\ge d_1+1$
or
![]() $|T_2|\ge d_2+1$
. By the given condition of
$|T_2|\ge d_2+1$
. By the given condition of
![]() $f_j$
being locally degree
$f_j$
being locally degree
![]() $d_j+1$
, we see one of the two terms in (D·2) is always 0. The result follows.
$d_j+1$
, we see one of the two terms in (D·2) is always 0. The result follows.
Acknowledgements
We thank Zach Hunter for various minor corrections.